2020牛客寒假算法基础集训营1

C umi和弓道

链接：https://ac.nowcoder.com/acm/contest/3002/C
来源：牛客网

umi对弓道非常痴迷。
有一天，她在研究一个射箭问题：
在一个无限大的平面中，她站在 $(x_0,y_0)$ 这个坐标。
有$n$个靶子，第$i$ 个靶子的坐标是
umi准备在$x$轴或 $y$ 轴上放置一块挡板来挡住弓箭的轨迹，使得她可以射中的靶子数量不超过 $k$ 个。
她想知道挡板的最短长度是多少？
注：假定弓箭的轨迹是起点为umi坐标、长度无穷大的射线。umi和靶子的体积可以无视。挡板的边缘碰到弓箭轨迹也可视为挡住弓箭。
注2：挡板不能弯折，起始和终点必须在同一坐标轴上。

题解

不要想难,根据题意即可知,板子要么在x轴上,要么在y轴上
就求x轴的交点,然后算能否有长度$l$的板子符合题意
求$y$轴的交点,然后算是否有长度$l$的板子符合题意

#pragma comment(linker, "/STACK:102400000,102400000")
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
#include <ext/pb_ds/priority_queue.hpp>
using namespace std;
using namespace __gnu_pbds;
const double pi = acos(-1.0);
const double eps = 1e-12;
typedef long long ll;
const int MAXN = 1e5 + 10;
 
typedef struct point vec;
struct point { //点的基本数据结构
    double x, y;
    double poe;
    int pos;
    point(double _x = 0, double _y = 0)
        : x(_x)
        , y(_y)
    {
    }
    double len() //模长
    {
        return sqrt(x * x + y * y);
    }
    vec chuizhi()
    {
        return vec(-y, x);
    }
    double operator*(const point& i_T) const //点积
    {
        return x * i_T.x + y * i_T.y;
    }
    double operator^(const point& i_T) const //叉积
    {
        return x * i_T.y - y * i_T.x;
    }
    point operator*(double u) const
    {
        return point(x * u, y * u);
    }
    bool operator==(const point& i_T) const
    {
        return fabs(x - i_T.x) < eps && fabs(y - i_T.y) < eps;
    }
    point operator/(double u) const
    {
        return point(x / u, y / u);
    }
    point operator+(const point& i_T)
    {
        return point(x + i_T.x, y + i_T.y);
    }
    point operator-(const point& i_T)
    {
        return point(x - i_T.x, y - i_T.y);
    }
    friend bool operator<(point a, point b)
    {
        return fabs(a.y - b.y) < eps ? a.x < b.x : a.y < b.y;
    }
    void atn2()
    {
        poe = atan2(y, x);
    }
    friend ostream& operator<<(ostream& out, point& a)
    {
        //cout << a.x << ' ' << a.y;
        printf("%.8f %.8f", a.x, a.y);
        return out;
    }
    friend istream& operator>>(istream& in, point& a)
    {
        scanf("%lf%lf", &a.x, &a.y);
        return in;
    }
};
point p[MAXN];
int n;
vector<double> xx, yy;
int bijiao(double x, double y)
{
    if (fabs(x - y) < eps)
        return 0;
    if (x > y)
        return 1;
    return -1;
}
double INF = 1e30;
int main()
{
    int k;
    cin >> p[0];
    cin >> n >> k;
    int m = n - k;
    for (int i = 1; i <= n; i++)
        cin >> p[i];
    for (int i = 1; i <= n; i++) {
        if (p[i].x * p[0].x > 0)
            yy.push_back(INF);
        else
            yy.push_back(p[i].y - p[i].x * (p[0].y - p[i].y) / (p[0].x - p[i].x));
    }
    for (int i = 1; i <= n; i++) {
        if (p[i].y * p[0].y > 0)
            xx.push_back(INF);
        else
            xx.push_back(p[i].x - (p[i].y * (p[0].x - p[i].x) / (p[0].y - p[i].y)));
    }
    sort(xx.begin(), xx.end());
    sort(yy.begin(), yy.end());
    double minn = INF;
    for (int i = 0; i + m - 1 < xx.size(); i++) {
        if (bijiao(xx[i], INF) == 0)
            break;
        minn = min(minn, xx[i + m - 1] - xx[i]);
    }
    for (int i = 0; i + m - 1 < yy.size(); i++) {
        if (bijiao(yy[i], INF) == 0)
            break;
        minn = min(minn, yy[i + m - 1] - yy[i]);
    }
    if (bijiao(minn, INF) == 0)
        cout << -1 << endl;
    else
        printf("%.7fn", minn);
    return 0;
}

F maki和tree

链接：https://ac.nowcoder.com/acm/contest/3002/F
来源：牛客网

有一天，maki拿到了一颗树。所谓树，即没有自环、重边和回路的无向连通图。
这个树有$n$个顶点，$n-1$ 条边。每个顶点被染成了白色或者黑色。
maki想知道，取两个不同的点，它们的简单路径上有且仅有一个黑色点的取法有多少？
注：
①树上两点简单路径指连接两点的最短路。
② 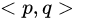和 的取法视为同一种。

题解

对于一个黑色的点,其对应的路径取法,是与它相连的白色点联通块$f[i]$有关的
即${\sum }_1^k{\sum }_i^{k}f[i]\ast f[j]+{\sum }_1^{k}f[i]$
然后求相连的联通块大小,用dfs也行,并查集也行

#pragma comment(linker, "/STACK:102400000,102400000")
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
#include <ext/pb_ds/priority_queue.hpp>
using namespace std;
using namespace __gnu_pbds;
const double pi = acos(-1.0);
const double eps = 1e-8;
typedef long long ll;
const ll INF = LLONG_MAX;
const ll ENF = LLONG_MIN;
const int MAXN = 1e6 + 10;
const int inf = __INT_MAX__;
const int enf = INT_MIN;

char s[MAXN];
vector<int> e[MAXN];
int f[MAXN], si[MAXN];
int fa(int x)
{
    return f[x] = (x == f[x] ? x : fa(f[x]));
}
vector<int> v;
int main()
{
    int n;
    cin >> n;
    cin >> (s + 1);
    for (int i = 1; i <= n; i++) {
        if (s[i] == 'B') {
            v.push_back(i);
            continue;
        }
        f[i] = i;
        si[i] = 1;
    }
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        if (s[x] == 'B' && s[y] == 'B')
            continue;
        e[x].push_back(y);
        e[y].push_back(x);
        if (s[x] == 'B' || s[y] == 'B')
            continue;
        int fx = fa(x), fy = fa(y);
        if (fx == fy)
            continue;
        f[fy] = fx;
        si[fx] += si[fy];
    }
    ll sum = 0;
    for (auto it : v) {
        vector<int> a;
        for (auto jt : e[it])
            a.push_back(si[fa(jt)]);

        int num = a.size();
        for (int i = 0; i < num; i++) {
            sum += a[i];
            for (int j = i + 1; j < num; j++)
                sum += a[i] * a[j];
        }
    }
    cout << sum << endl;
    return 0;
}

最后

以上就是雪白路灯为你收集整理的2020牛客寒假算法基础集训营1的全部内容，希望文章能够帮你解决2020牛客寒假算法基础集训营1所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。