NEUQ-ACM预备队-双周赛_37-1 打字7-2 分香肠7-3 会议安排7-4 神秘密码7-5 国王游戏

7-1 打字

题目

思路

打表？

代码

#include<iostream>
#include<string>
#include<cstring>
using namespace std;
int ans[8];
char c;
string tem;
int main()
{
	
	cin >> tem;
	for (int i = 0; i < tem.length();i++)
	{
		c = tem[i];
		if (c == '`' || c == '1' || c == 'q' || c == 'Q' || c == 'a' || c == 'A' || c == 'Z' || c == 'z')
		{
			ans[0]++;
		}
		else if (c == '2' || c == 'w' || c == 'W' || c == 's' || c == 'S' || c == 'X' || c == 'x')ans[1]++;
		else if ((c == '3' || c == 'e' || c == 'd' || c == 'c' || c == 'E' || c == 'D' || c == 'C'))ans[2]++;
		else if (c == '4' || c == 'r' || c == 'f' || c == 'v' || c == 'R' || c == 'F' || c == 'V')ans[3]++;
		else if (c == '5' || c == 't' || c == 'g' || c == 'b' || c == 'T' || c == 'G' || c == 'B')ans[3]++;
		else if (c == '6' || c == 'Y' || c == 'H' || c == 'N' || c == 'U' || c == 'J' || c == 'M')ans[4]++;
		else if (c == '7' || c == 'y' || c == 'h' || c == 'n' || c == 'u' || c == 'j' || c == 'm')ans[4]++;
		else if (c == '8' || c == 'i' || c == 'k' || c == ',' || c == 'I' || c == 'K' || c == '<')ans[5]++;
		else if (c == '9' || c == 'o' || c == 'l' || c == '.' || c == 'O' || c == 'L' || c == '>')ans[6]++;
		else ans[7]++;
	}

	//ans[7] -= 1;
	for (int i = 0; i < 8; i++)printf("%dn", ans[i]);
	return 0;
}

7-2 分香肠

题目

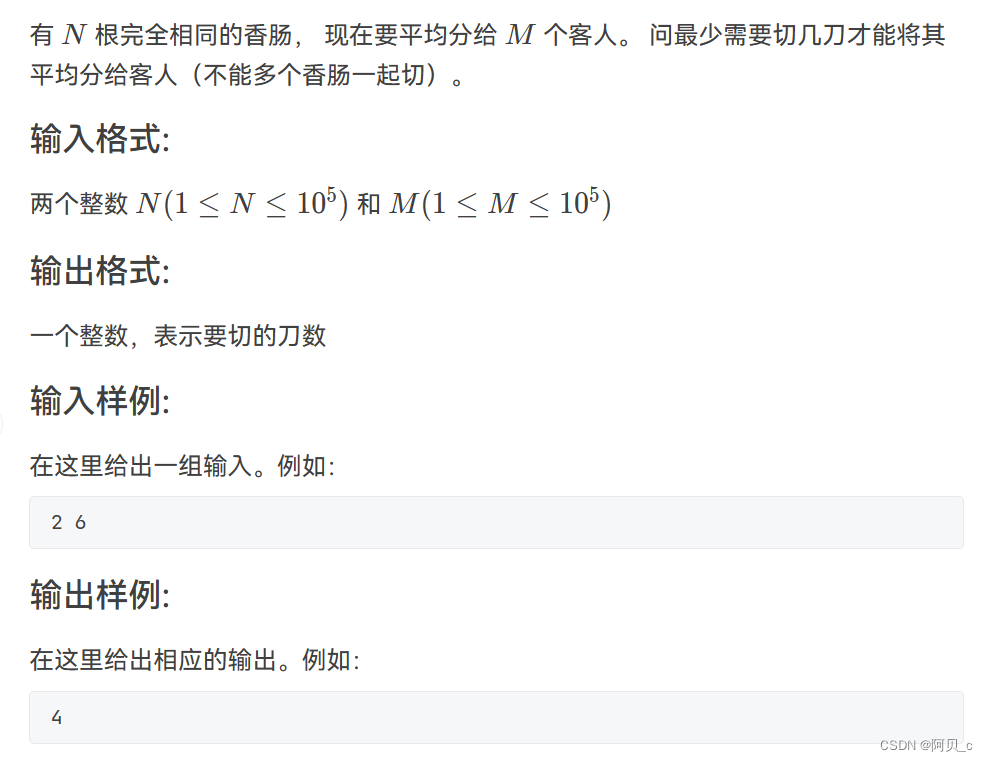
思路

面向题解编程

将香肠排列成一条直线，一条接着一条（从而获得由N个较短线段组成的线段）。将这条线切割成M个相等的线段可以得到所需的解。虽然我们在概念上做的是M-1切，但其中一些不是真正的切，而是落在香肠之间（较短的线段）。
例如，对于两条香肠和四个品尝者，第一次切是真实的，将第一条香肠分成两半，第二次切不是真实的，因为它实际上在两条香肠之间，第三次切是真的，将第二条香肠分成一半。
因此，我们可以简单地使用for循环来检查，对于对于每一次切割，它是真切割还是原本中间就是分开的。

另外，有一个明确的公式：解=M-gcd(N，M) （gcd即最大公约数）

代码

#include<bits/stdc++.h>
using namespace std;
int n, m;

int Gcd(int a, int b)
{
    if (b == 0)
    {
        return a;
    }
    else
    {
        return Gcd(b, a % b);
    }
}

int main()
{
    cin >> n >> m;
    cout << m - Gcd(m, n) << endl;
    return 0;
}

7-3 会议安排

题目

2
2

思路

线段重叠的最优解（大佬如是说）

代码

#include<bits/stdc++.h>
using namespace std;
struct segment {
	int st;
	int ed;
};
const int maxn = 1e4 + 5;
struct segment arr[maxn];

bool cmp(struct segment a, struct segment b)
{
	return a.ed < b.ed;
}
int T;
int n;
int main()
{
	cin >> T;
	while (T--)
	{
		cin >> n;
		for (int i = 0; i < n; i++)
		{
			cin >> arr[i].st >> arr[i].ed;
		}
		sort(arr, arr + n, cmp);
		int cnt = 0, now = 0;
		for (int i = 0; i < n; i++)
		{
			if (arr[i].st >= now)
			{
				now = arr[i].ed;
				cnt++;
			}
		}
		printf("%dn", cnt);
	}
	return 0;
}

7-4 神秘密码

题目

思路

递归啦递归啦（参考大佬代码）

代码

#include<bits/stdc++.h>
using namespace std;

string Code()
{
	string ans, temp;
	int num;
	char c;
	while (cin >> c)
	{
		if (c == '[')
		{
			cin >> num;
			temp = Code();
			while (num--)ans += temp;
		}
		else if (c == ']')
		{
			return  ans;
		}
		else
			ans += c;
	}
	return ans;
}
int main()
{
	cout << Code() << endl;
	return 0;
}

7-5 国王游戏

题目

恰逢 H 国国庆，国王邀请 $n$ 位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这 $n$ 位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。

输入格式

第一行包含一个整数 $n$，表示大臣的人数。

第二行包含两个整数 $a$ 和 $b$，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来 $n$ 行，每行包含两个整数 $a$ 和 $b$，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

输出格式

一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

样例 #1

样例输入 #1

3 
1 1 
2 3 
7 4 
4 6

样例输出 #1

2

提示

【输入输出样例说明】

按 $1$、$2$、$3$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $1$、$3$、$2$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $2$、$1$、$3$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按$ 2$、$3$、$1 $这样排列队伍，获得奖赏最多的大臣所获得金币数为 $9$；

按 $3$、$1$、$2 $这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按$ 3$、$2$、$1$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $9$。

因此，奖赏最多的大臣最少获得 $2$ 个金币，答案输出 $2$。

【数据范围】

对于 $20\%$ 的数据，有 $1\le n\le 10,0<a,b<8$；

对于 $40\%$ 的数据，有$ 1≤ n≤20,0 < a,b < 8$；

对于 $60\%$ 的数据，有 $1\le n\le 100$；

对于 $60\%$ 的数据，保证答案不超过 $10^9$；

对于 $100\%$ 的数据，有 $1\le n\le 1,000,0<a,b<10000$。

NOIP 2012 提高组 第一天 第二题

思路

贪心+高精

代码

#include<bits/stdc++.h>
using namespace std;

struct core {
	int l;
	int r;
};
int n;
struct core arr[1005];
bool cmp(struct core a, struct core b)
{
	return a.l * a.r < b.l* b.r;
}

int a[10000],b[10000], ans[10000];
int alen;
int len;
int main()
{
	cin >> n;
	cin >> arr[0].l >> arr[0].r;
	for (int i = 1; i <= n; i++)
	{
		cin >> arr[i].l >> arr[i].r;
	}
	sort(arr + 1, arr + 1 + n, cmp);
	//初始化
	a[alen++] = 1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j < alen; j++)
		{
			a[j] *= arr[i - 1].l;
		}
		for (int j = 0; j < alen; j++)
		{
			int temp = a[j] / 10;
			if (temp)
			{
				a[j + 1] += temp;
				if (j == alen - 1)
				{
					alen++;
				}
			}
			a[j] %= 10;
			b[j] = a[j];
		}
		for (int j = alen - 1; j >= 0; j--)
		{
			int temp = b[j];
			b[j] = temp / arr[i].r;
			if (j > 0)
			{
				b[j - 1] += 10 * (temp % arr[i].r);
			}
		}
		int flag = false;
		for (int j = alen - 1; j >= 0; j--)
		{
			if (b[j] > ans[j])
			{
				flag = true;
				break;
			}
			else if (b[j] < ans[j])
			{
				flag = false;
				break;
			}
		}
		if (flag)
		{
			for (int j = alen - 1; j >= 0; j--)
			{
				ans[j] = b[j];
			}
		}
	}
	while (ans[alen-1] == 0)alen--;
	for (int i = alen - 1; i >= 0; i--)
	{
		printf("%d", ans[i]);
	}
	return 0;
}

后记

是的！这道题虽然很难但是思路就是酷酷的只有五个字！身为蒟蒻的我使用数组法模拟高精度数将此题解出是非常开心的！！！但是值得指出的是，我最开始陷入了使用类似邻接表的方式将每一位大臣获得的金子数都一股脑存储下来，而限于代码能力与习惯，并不擅长用函数抽象的我在整个过程中受到了N多的阻力，最终选择放弃使用模拟的方式，转而走向了使用高精度数类的方式，准备CV他人代码时，仔细阅读某大犇的思路，我发现并不需要存储全部大臣的金子数，在不除去本人右手数字的情况下，得到的数组是完全一致的，因此，只需要使用a来存储不出去本人右手的数字数组，用b来临时存储此人实际的金币数，再与ans比较大小更新ans即可！！！！至此！！！耗时良久一度试图放弃的题目被成功AC！！开心到拍手！

最后

以上就是淡然蚂蚁为你收集整理的NEUQ-ACM预备队-双周赛_37-1 打字7-2 分香肠7-3 会议安排7-4 神秘密码7-5 国王游戏的全部内容，希望文章能够帮你解决NEUQ-ACM预备队-双周赛_37-1 打字7-2 分香肠7-3 会议安排7-4 神秘密码7-5 国王游戏所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。