HDU 5794 A Simple Chess （dp+Lucas组合数取模）

56 阅读 0 评论 37 点赞

我是靠谱客的博主激昂鲜花，最近开发中收集的这篇文章主要介绍HDU 5794 A Simple Chess （dp+Lucas组合数取模），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目链接
这道题目和 CF #313 (Div. 2) E. Gerald and Giant Chess是姊妹题，做法基本一致，不同点事本题走法是“日”的走法，依旧是只能往右下方向。所以需要写一个函数计算(x,y)是否可达，以及有几种走法。
见图：
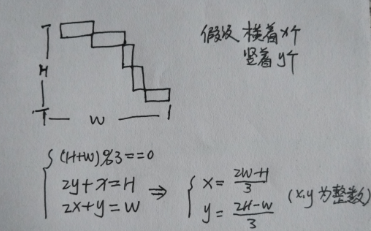
这里写图片描述
然后就和CF那道题一样的解法了


#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<cstdlib>
#include<vector>
using namespace std;
#define cl(a,b) memset(a,b,sizeof(a))
#define LL long long
#define pb push_back
#define gcd __gcd

#define For(i,j,k) for(int i=(j);i<k;i++)
#define lowbit(i) (i&(-i))
#define _(x) printf("%dn",x)

const int maxn = 110119*2+10;// p * 2
const int inf  = 1 << 28;
LL p = 110119;

LL fac[maxn],inv[maxn];

LL qsm(LL a, LL b){
    LL ans = 1;
    while(b){
        if(b&1)ans = ans*a%p;
        a = a*a%p;
        b>>=1;
    }
    return ans%p;
}

LL Lucas(LL n, LL m){//非递归，合并C函数
    LL ans = 1;
    while(n&&m){
        LL x = n%p;
        LL y = m%p;
        if(x<y)return 0;
        ans = (ans *( fac[x] * inv[y] *inv[x-y] % p ) %p )%p;
        n/=p;m/=p;
    }
    return ans%p;
}

void init(){//预处理出阶乘，逆元
    fac[0]=inv[0]=1;
    for(int i=1;i<maxn;i++){
        fac[i] = (fac[i-1]*i)%p;
        inv[i]=qsm(fac[i],p-2)%p;
    }
}

LL dp[maxn];
pair<LL,LL> point[maxn];
LL n,m,k;

pair<LL,LL> getdis(LL H,LL W){
    if((H+W)%3!=0)return make_pair(-1,-1);
    if((W*2-H)%3!=0||(2*H-W)%3!=0)return make_pair(-1,-1);
    if(W*2-H<0||H*2-W<0)return make_pair(-1,-1);
    return make_pair((W*2-H)/3+(H*2-W)/3,(W*2-H)/3);
}
int main(){
    init();int cas = 1;
    while(~scanf("%lld%lld%lld",&n,&m,&k)){
        bool flag = false;
        for(int i=0;i<k;i++){
            scanf("%lld%lld",&point[i].first,&point[i].second);
            if(point[i].first==n&&point[i].second==m)flag=true;
            point[i].first--;point[i].second--;
        }

        if(flag){
            printf("Case #%d: 0n",cas++);continue;
        }
        point[k].first = n-1;
        point[k++].second = m-1;

        sort(point,point+k);
        pair<LL,LL> dis;
        //dp[0]=0;
        cl(dp,0);
        for(int i=0;i<k;i++){
            dis = getdis(point[i].first,point[i].second);
            if(dis.first==-1)continue;
            dp[i] = Lucas(dis.first,dis.second);

            for(int j=0;j<i;j++){
                LL dx = point[i].first - point[j].first;
                LL dy = point[i].second - point[j].second;
                if(dx<0||dy<0)continue;
                dis = getdis(dx,dy);
                if(dis.first==-1)continue;
                dp[i] = (dp[i] - dp[j]*Lucas(dis.first,dis.second)%p)%p;
            }
            dp[i] = (dp[i]+p)%p;
        }

        printf("Case #%d: %lldn",cas++,dp[k-1]+p%p);

    }
    return 0;
}