【算法】合并排序问题1. 问题描述2. 问题分析3. 时间复杂度分析4. 实验代码5. 实验结果参考与致谢

72 阅读 0 评论 48 点赞

我是靠谱客的博主高兴泥猴桃，最近开发中收集的这篇文章主要介绍【算法】合并排序问题1. 问题描述2. 问题分析3. 时间复杂度分析4. 实验代码5. 实验结果参考与致谢，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 问题描述

复现合并排序问题，用用分治算法来解决这个问题，并分析其时间复杂度。

2. 问题分析

用分治算法来解决这个问题，以下是分治算法的基本思路：

把原问题分解成若干个子问题
递归求每一个子问题的解
合并子问题的解

在合并排序中:
输入: 给定的n 个元素的序列A
输出为：A[0] <= A[1] <= A[2] <=…<= A[n-1]

用分治算法的思路来考虑此问题:
1.我们的目标是把乱序的数组A 变成有序的sorted A，将问题分解，把A 沿中间切分
在这里插入图片描述
2.这样问题一分为二，
Problem1 : LA− > SortedLA
Problem2 : RA− > SortedRA

假设合并函数为MergeSort(A)，那么
SLA = MergeSort(LA) <= Problem1
RLA = MergeSort(RA) <= Problem2

3.合并子问题
合并(SLA,SRA) = SA, 把两个有序的子序列合并成一个序列。

3. 时间复杂度分析

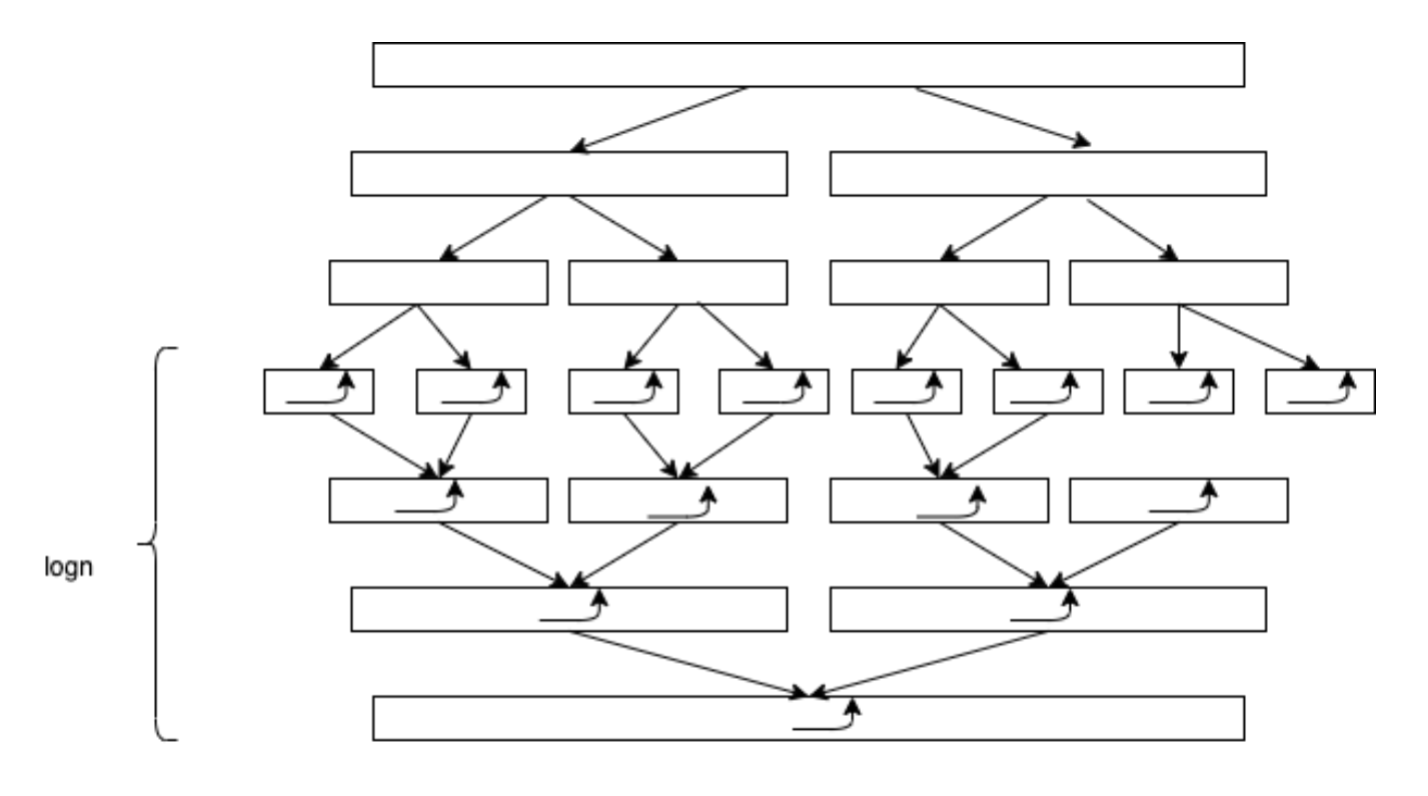
在这里插入图片描述
由图表可知合并排序的计算流程，在合并时，每一层的比较次数是n，一共有logn 层，由此可得，该排序的时间复杂度是O（nlogn）。
在做合并的时候将有序的特征进行传递，因此得到了性能的提升。

4. 实验代码

import   time 
import   random
import   matplotlib . pyplot   as   plt import   numpy   as   np
from   scipy . optimize   import   curve_ fit


# 自 定 义 函 数 e 指 数 形 式
def func(x, a, b, c):
	return a* np. sqrt( x)*( b* np. square( x) +c)

def   random _ list( length ): 
	randomlist   =   []
	for i in range( length ): 
		randomlist. append ( i+1)
	random . shuffle( randomlist) 
	return   randomlist

# 生 成 随 机 数 组
def   random _ int_ list( start ,   stop ,   length ):
	start , stop = ( int( start), int( stop )) if start <= stop else ( int( stop ), int( start))
	length = int( abs( length )) if length else 0 
	random _ list   =   []
	for i in range( length ): random _ list. append ( random . randint( start ,   stop ))
	random _ list. sort () 
	return   random _ list


def   merge_ sort( A):
	if   len ( A)   <=   1: 
		return A
	else:
		mid   =   len ( A)   //2 
		LA   =   A[: mid ]
		RA   =   A[ mid :]
		SLA   =   merge_ sort( LA) 
		SRA   =   merge_ sort( RA) 
		SA   =   merge( SLA , SRA )
		return SA

def   merge(a, b): 
	result = [] 
	i=0
	j=0
	while   i<   len ( a)   and   j   <   len ( b): 
		if a[ i] < b[ j]:
			result. append ( a[ i]) 
			i = i + 1
		else:
			result. append ( b[ j]) 
			j = j + 1
	while   i   <   len ( a): 
		result. append ( a[ i]) 
		i = i + 1
	while   j   <   len ( b): 
		result. append ( b[ j]) 
		j = j + 1
	return result

if   __ name __   ==   "__ main __":
	x = [10 ,100 ,1000 ,10000 ,100000]
	time_ list   =   []
	for index in range( len ( x)): 
		average_ time   	=   []

		for i   in   range  (100): 
			# print(’ x:’, x[ index ])
			randomlist   =   random _ list( x[ index ])
			# randomlist   =   random _ int_ list(1 ,   x[ index ],   x[ index ]) 
			total_ time   =   0
			time_ start= time. time () 
			merge_ sort( randomlist) 
			time_ end = time. time ()
			total_ time   =   time_ end   -   time_ start 
			average_ time. append ( total_ time)
	# 求 平 均 值
	average   =   np. mean ( average_ time) 		
	time_ list. append ( average)
print( time_ list) 

# 用matplotlib 画 图 
# plt. figure ()
# plt. plot(x, time_list , marker=’*’, label   =   " merge   sort ") 
# plt. show ()


# 定 义x 、 y 散 点 坐 标

x = np. array ( x) 
num   =   time_ list
y = np. array ( num )

# 非 线 性 最 小 二 乘 法 拟 合
popt , pcov = curve_ fit( func , x, y) 

# 获 取 popt 里 面 是 拟 合 系 数
print( popt)
a = popt [0] 
b = popt [1] 
c = popt [2]
yvals = func(x,a,b, c) # 拟 合y 值
print(’ popt:’, popt)
print(’ 系 数a:’, a)
print(’ 系 数b:’, b)
print(’ 系 数 c:’, c) 
print(’ 系 数pcov :’, pcov )
print(’ 系 数 yvals:’, yvals) 

# 绘图
plot 1   =   plt. plot(x,   y,   ’s’, label=’ original   values ’) 
plot 2   =   plt. plot(x,   yvals ,   ’r’, label=’ polyfit   values ’) plt. xlabel(’x ’)
plt. ylabel(’y ’)
plt. legend ( loc =4) # 指 定legend 的 位 置 右 下 角
plt. title(’ curve_fit ’) 
plt. show ()

5. 实验结果

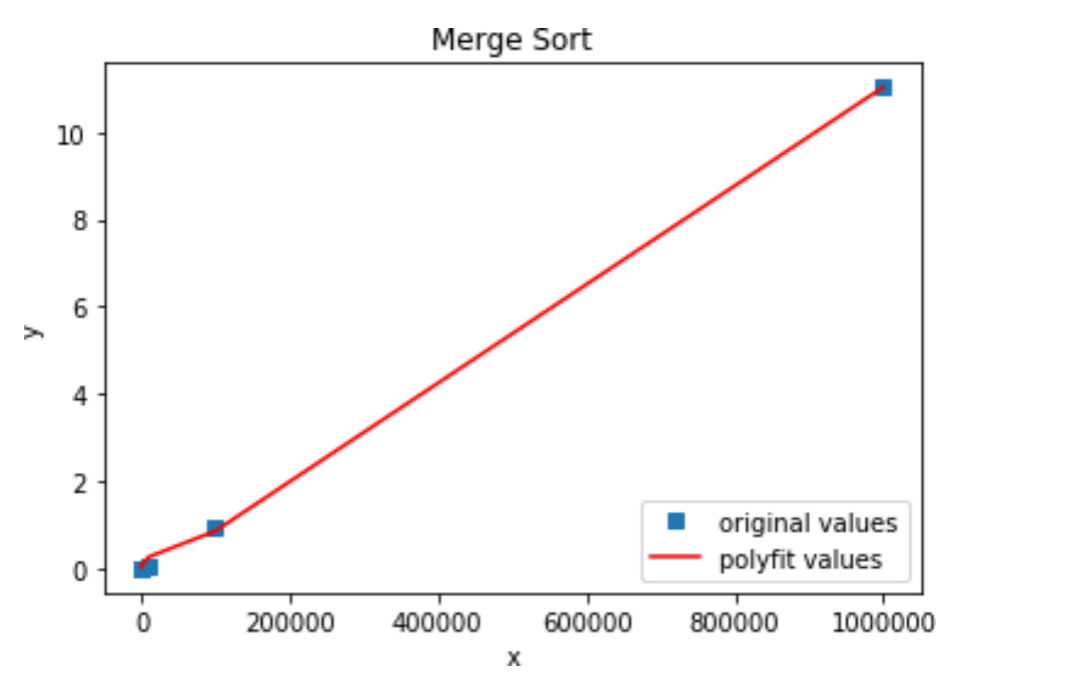
在这里插入图片描述
计算不同范围大小下的随机数组进行合并排序所要消耗的时间，在多次实验求平均值，并对图像进行拟合处理后，得到上述图像。可以看到，合并排序的时间复杂度图像近似于 nlogn，这与我们理论验证的结果相同。

参考与致谢

算法分析和设计 http://www.icourse163.org/spoc/learn/ZJUT- 1460190163?tid=1460863458#/learn/content?type=detail&id=1238944804&sm=1
python 中任意曲线的拟合方法 https://blog.csdn.net/changdejie/article/details/83089933