原题链接Median of Two Sorted Arrays
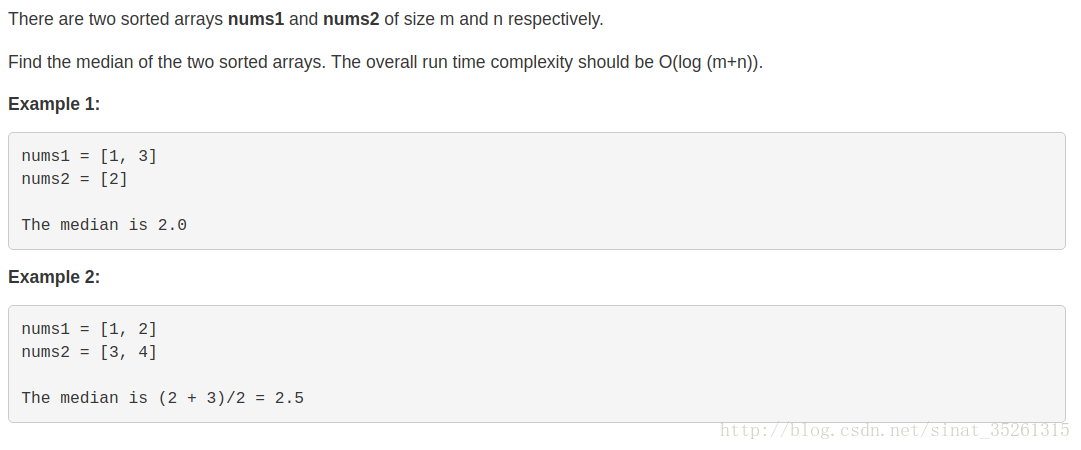
意思是给定两个有序序列,找到合并之后的中位数,要求复杂度O(log(m+n))。扩展方面,找到合并之后第K小的数,因为中位数也符合第K小范畴,所以直接按照后者解题即可
不考虑复杂度的情况下,首先想到的方法是一次从两个数组中选取较小的那个,直到选取第k个,此种方法复杂度在O(k),代码如下
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int lhs_idx = 0;
int rhs_idx = 0;
/* 奇数偶数时中位数计算方法不同 */
int total = nums1.size() + nums2.size();
if(total % 2 == 0)
{
return (findKth(nums1, nums2, total / 2) + findKth(nums1, nums2, total / 2 + 1)) / 2.0;
}
else
{
return findKth(nums1, nums2, total / 2 + 1) / 1.0;
}
}
int findKth(vector<int>& nums1, vector<int>& nums2, int k)
{
int ans = 0;
int lhs_idx = 0;
int rhs_idx = 0;
/* 复杂度体现处,遍历k次,所以为O(k) */
while(k--)
{
/* 需要考虑边界情况 */
if(lhs_idx >= nums1.size() && rhs_idx < nums2.size())
ans = nums2[rhs_idx++];
else if(lhs_idx < nums1.size() && rhs_idx >= nums2.size())
ans = nums1[lhs_idx++];
else if(lhs_idx >= nums1.size() && rhs_idx >= nums2.size())
return -1;
else if(nums1[lhs_idx] < nums2[rhs_idx])
ans = nums1[lhs_idx++];
else
ans = nums2[rhs_idx++];
}
return ans;
}
};
接下来想办法达到O(log(m+n)),涉及到log通常会考虑二分法,所以优化需要在findKth()函数中采用二分法计算。下面把nums1看成数组A,nums2看成数组B,A的大小为m,B的为n
既然需要找到第K小的数,那么首先考虑A的第k/2个元素和B的第k/2个元素。这么考虑是因为
- 既然采用二分法,那么使用时通过二分就一定可以把结果的范围缩小
具体说明,
如果A[k/2] > B[k/2],说明B的前k/2个元素在合并A,B之后的前k个位置
- 因为A[k/2]] > B[k/2],那么假设A[i] == B[k/2],i一定小于k/2,显然此时A的前i个,B的前k/2个元素一定都是组成合并之后前k小元素的成员,所以B的前k/2个元素一定都是前k个元素的成员
- 所以此时就已经找到了k/2个元素了,只需再找k/2个最小的元素即可,而这些元素都在B的[k/2, n)和A中,很明显可以利用递归,此时k改为k/2
如果A[k/2] <= B[k/2],在A的[k/2,m)和B中查找剩下的k/2个元素,原理同上
代码如下
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size();
int n = nums2.size();
int total = m + n;
if(total % 2 == 0)
{
return (findKth(nums1, nums2, total / 2) + findKth(nums1, nums2, total / 2 + 1)) / 2.0;
}
else
{
return findKth(nums1, nums2, total / 2 + 1) / 1.0;
}
}
int findKth(vector<int> A, vector<int> B, int k)
{
/* 总是让A的大小小于B */
if(A.size() > B.size())
return findKth(B, A, k);
if(A.size() == 0)
return B[k - 1];
if(k == 1)
return std::min(A[0], B[0]);
int m = A.size();
int n = B.size();
/* 如果大小不足k/2,取自身大小 */
/* 因为有这种情况,后面不一定是k/2,所以递归调用时是k - j/k - i */
int i = std::min(m, k / 2);
int j = std::min(n, k / 2);
if(A[i - 1] > B[j - 1])
{
return findKth(A, std::vector<int>(B.begin() + j, B.end()), k - j);
}
else
{
return findKth(std::vector<int>(A.begin() + i, A.end()), B, k - i);
}
}
};准确说这种方法没有达到O(log(m+n)),但是更具通用性,可以计算不仅仅是中位数,还可以计算第k小元素,效率相对更高。
不过就本题而言,每次二分AB中间的位置,根据大小关系抛弃小方的左端以及大方同样长度的右端,以达到最后的结果,但是没有什么通用性,只可以计算中位数
最后
以上就是明亮麦片最近收集整理的关于每天一道LeetCode-----两个有序数组合并后的第K个数的全部内容,更多相关每天一道LeetCode-----两个有序数组合并后内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复