12.降维总结

1.降维

  第二种学习的无监督算法叫做降维。降维的作用有几个，比如说数据压缩，使数据占用更少的内存空间，有时还能给算法提速。

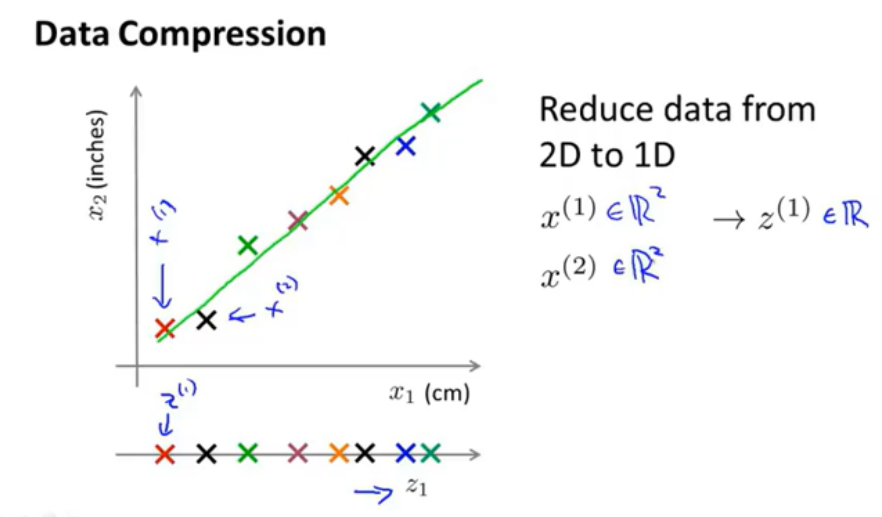
  如图所示就是一种降维的实例，它将一片二维空间中的实例用一条直线近似代表，最后将一片二维数据近似为一维直线上的数据。

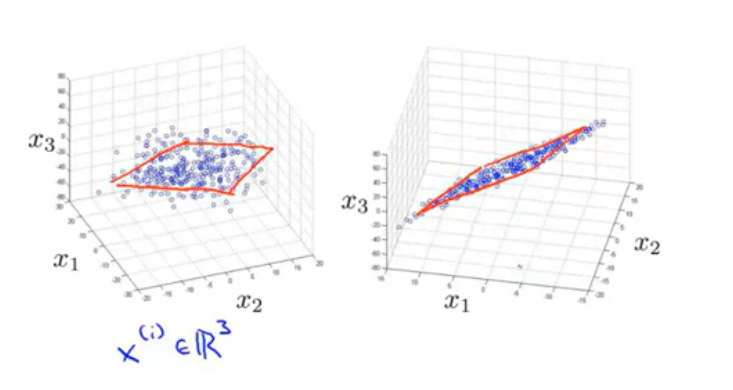
              三维降到二维

2.PCA算法

  目前，最常用的算法是主成分分析法（Principal Componet Analysis, PCA）。

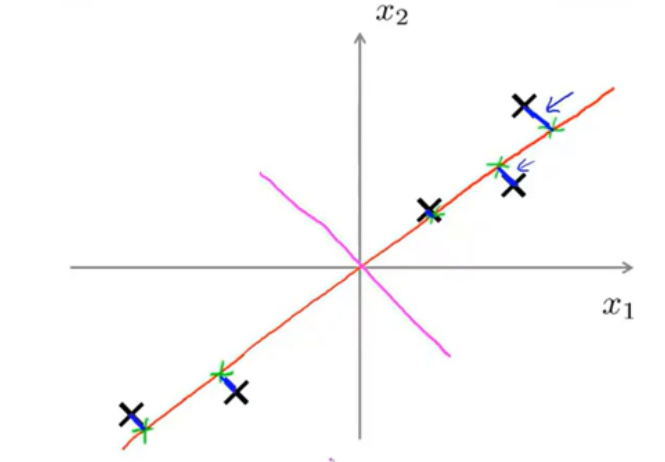
  以二维为例说明PCA的作用；如图所示，×代表二维样本点，而降维的作用就是将这些样本点投影到一条一维直线上——比如橙色的直线，其中蓝色的短线是样本点离这条直线的距离，这个距离叫投影误差，它说明了降维时产生的误差。
  假设有另外一条粉色直线，通过计算可以发现其他样本点在这条直线上的投影误差会比在橙色直线上的投影误差要大得多吗，显然，粉色直线的降维效果没有橙色直线好。PCA算法的工作就是找到一条投影误差最小的直线。
  需要注意的是，与线性回归相比，线性回归的代价函数计算的是样本点到假设函数的垂直距离，而PCA的代价函数是样本点到降维函数的正交距离。
  PCA的步骤：
1.首先对数据进行归一化和特征缩放处理。
2.计算数据的协方差矩阵

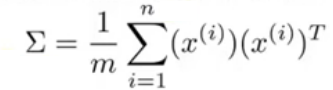
3.结算协方差矩阵的特征向量，这个特征向量就是低维投影向量。
  可以使用奇异值分解的方法简化计算，利用函数[U,S,V] = svd(Sigma);其中的u矩阵就是我们需要的特征向量，取前k列形成新矩阵$u_{reduce}$。有公式可算出z向量：

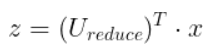
  倒用此公式可以还原出压缩前的数据。

3.低维空间选择

  降到多少维主要看需求，看所需要保留主成分的数量。这个数量由下式计算。

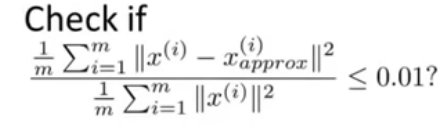
  $x_{approx}^{(i)}$是值降到k维时x的近似点，一般要求保留99%的数据此时就要这个误差值小于1%。具体过程是不断改变k值直到误差值合格为止。

4.PCA的具体用法

  运用PCA对于训练模型的精度影响不大，因此可以先降低精度再训练模型，这能有效增加训练效率。在实际使用中，应该先用原始数据尝试训练一下，如果训练速度特别慢，这时候可以考虑用PCA压缩数据。
  PCA在几个方面表现不好，比如说解决过拟合，这是因为PCA只是相当于将某些影响因素忽略掉了，对于过拟合的产生可以说毫无影响。

总结

  本章学习了如何使用PCA算法降维，以及PCA算法的各种用法。

最后

以上就是飞快戒指为你收集整理的12.降维总结的全部内容，希望文章能够帮你解决12.降维总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。