文章目录
- 引论
- 语法描述
- 词法分析
- 语法分析
- 自上向下分析
- 自下向上分析
- 属性文法
- 语义分析和是中间代码产生
- 优化
- 目标代码生成

引论
- 编译程序运行框架
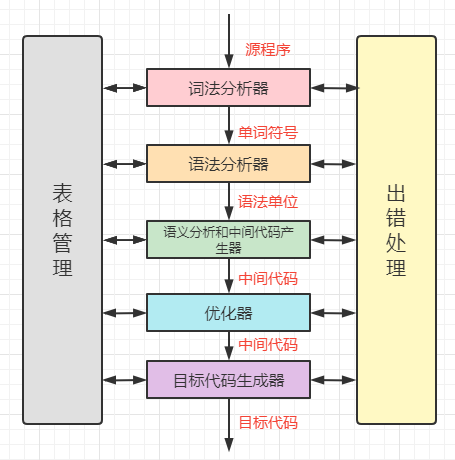
| 词法分析器 | 输入源程序,进行词法分析,输出单词符号。 |
|---|---|
| 语法分析器 | 对单词符号串进行语法分析,识别出各类语法单位 |
| 语义分析与中间代码产生器 | 按语义规则对归约出的语法单位进行语义分析并翻译成中间代码。 |
| 优化器 | 对中间代码进行优化处理 |
| 目标代码生成器 | 把中间代码翻译成目标程序 |
| 表格管理 | 登记源程序的各类信息和编译各阶段的进展情况 |
| 出错处理 | 对出现在源程序中的错误进行处理 |
- 编译前端和后端
- 前端
主要由与源语言有关但与目标机无关的那些部分(词法分析、语法分析、语义分析、中间代码产生)组成,有的代码优化工作也给包括在前端。 - 后端
包括编译程序中与目标机有关的那些部分(与目标机有关的代码优化、目标代码生成),后端通常依赖中间语言而不是源语言。
-
编译过程五个阶段
词法分析、语法分析、语义分析与中间代码产生、优化、目标代码生成。
前四个阶段与硬件无关,最后一个阶段与硬件有关。 -
汇编语言和高级语言的区别
汇编语言跟机器指令一一对应,高级语言不跟机器指令一一对应。
语法描述
- 乔姆斯基四型文法
乔姆斯基(Chomsky)把文法分成四种类型,即0型、1型、2型和3型。0型强于1型,1型强于2型,2型强于3型。这几类文法的差别在于对产生式加不同的限制。
| 0型 | 短语文法 | 能力相当于图灵机,都是递归可枚举的 |
|---|---|---|
| 1型 | 上下文有关法 | 即替换非终结符时考虑上下文 α alpha α和 β beta β, α A β → α γ β alpha Abeta→alphagammabeta αAβ→αγβ |
| 2型 | 上下文无关法 | 即无需考虑上下文 |
| 3型 | 右线性文法 | 另一种形式左线性文法,也称正规文法, A → B α A→Balpha A→Bα或 A → α A→alpha A→α |
-
上下文无关法
一个上下文无关法G是一个四元式 G = ( V T , V N , S , P ) G=(V_T,V_N,S,P) G=(VT,VN,S,P),其中
V T V_T VT:终结符集合(非空)
V N V_N VN:非终结符集合(非空),且 V T ∩ V N = ∅ V_Tcap V_N=varnothing VT∩VN=∅
S S S:文法的开始符号, S ∈ V N Sin V_N S∈VN
P P P:产生式集合(有限),每个产生式形式为 P → α , P ∈ V N , α ∈ ( V T ∪ V N ) ∗ Prarralpha,Pin V_N,alphain (V_Tcup V_N)^* P→α,P∈VN,α∈(VT∪VN)∗,开始符 S S S至少必须在某个产生式的左部出现一次。 -
句型、句子
假定G是一个文法,S是它的开始符号,称 S ⟹ ∗ α Soverset{*}{implies}alpha S⟹∗α是一个句型,称仅含终结符的句型是一个句子。
btw,符号 ⟹ ∗ overset{*}{implies} ⟹∗指经过0步及以上推导;符号 ⟹ + overset{+}{implies} ⟹+指经过1步及以上推导;终结符指最终出现在程序中符号;非终结符是为了描述语法而创造出来的符号,不会出现在程序中。
例 ( i ∗ i + i ) (i*i+i) (i∗i+i)是文法G(E): E → i ∣ E + E ∣ E ∗ E ∣ ( E ) E→i|E+E|E*E|(E) E→i∣E+E∣E∗E∣(E)的一个句子,证明: E ⟹ ( E ) ⟹ ( E + E ) ⟹ ( E ∗ E + E ) ⟹ ( i ∗ E + E ) ⟹ ( i ∗ i + E ) ⟹ ( i ∗ i + i ) Eimplies(E)implies(E+E)implies(E*E+E)implies(i*E+E)implies(i*i+E)implies(i*i+i) E⟹(E)⟹(E+E)⟹(E∗E+E)⟹(i∗E+E)⟹(i∗i+E)⟹(i∗i+i) -
语言
文法G所产生的句子的全体就是一个语言,记为L(G), L ( G ) = { α ∣ S ⟹ + α & α ∈ V T ∗ } L(G)={alpha|Soverset{+}{implies}alpha&alphain{V_{T}^{*}}} L(G)={α∣S⟹+α&α∈VT∗}。
例文法G1:A→c|Ab的语言L(G1)={cbn|n≥0};
文法G2:S→AB,A→aA|a,B→bB|b的语言L(G2)={ambn|m,n≥1}。
词法分析
- 用状态图和正规式描述标识符
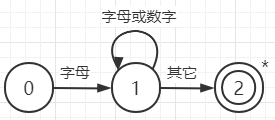
结点代表状态,用圆圈表示。状态之间用箭弧连结。箭弧上的标记(字符)代表在射出节点状态下可能出现得输入字符或字符类。
其中0为初态,2为终态(用双圈表示)。终态结上打个星号*意味着多读进了一个不属于标识符部分得字符,应把它退还给输入串。
令
Σ
=
{
A
,
B
,
0
,
1
}
Sigma={A,B,0,1}
Σ={A,B,0,1}
| 正规式 | 正规集 |
|---|---|
| (A|B)(A|B|0|1)* | Σ Sigma Σ上“标识符”的全体 |
| (0|1)(0|1)* | Σ Sigma Σ上“数”的全体 |
-
确定有限自动机(DFA)
一个确定有限自动机M是一个五元式 M = ( S , Σ , δ , s 0 , F ) M=(S,Sigma,delta,s_0,F) M=(S,Σ,δ,s0,F),其中
S S S:有穷状态集
Σ Sigma Σ:输入字母表(有穷)
δ delta δ:状态转换函数,为 S × Σ → S S×Sigmararr S S×Σ→S的单值部分映射, δ ( s , a ) = s ’ delta(s, a)=s’ δ(s,a)=s’表示:当现行状态为 s s s,输入字符为 a a a时,将状态转换到下一状态 s ’ s’ s’。我们把 s ’ s’ s’称为 s s s的一个后继状态。
s 0 ∈ S s_0in S s0∈S:初态(唯一)
F ⊆ S Fsube S F⊆S:终态集(可空) -
非确定有限自动机(NFA)
一个非确定有限自动机M是一个五元式 M = ( S , Σ , δ , S 0 , F ) M=(S,Sigma,delta,S_0,F) M=(S,Σ,δ,S0,F),其中
S S S:有穷状态集
Σ Sigma Σ:输入字母表(有穷)
δ delta δ: S × Σ ∗ → 2 S S×Sigma^*rarr2^S S×Σ∗→2S
S 0 ⊆ S S_0sube S S0⊆S:初态集(非空)
F ⊆ S Fsube S F⊆S:终态集(可空) -
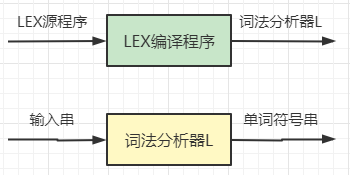
LEX
LEX用来描述和自动产生所需的各种词法分析器,包括正规式定义和识别规则两部分,将LEX程序编译后所得结果程序记为L,其作用同有限自动机一样,可用来识别和产生单词符号。
-
确定化和最小化
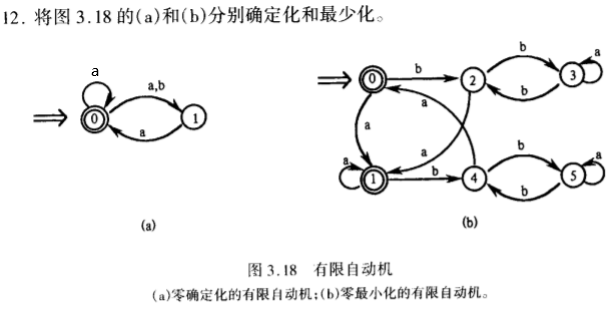
(a)确定化
| I | Ia | Ib |
|---|---|---|
| {0} | {0,1} | {1} |
| {0,1} | {0,1} | {1} |
| {1} | {0} | Φ varPhi Φ |
| Φ varPhi Φ | Φ varPhi Φ | Φ varPhi Φ |
如({0},a)={0,1}表示{0}只经过弧a可以到达{0,1},以此类推。
给状态编号
| s | a | b |
|---|---|---|
| 0 | 1 | 2 |
| 1 | 1 | 2 |
| 2 | 0 | 3 |
| 3 | 3 | 3 |
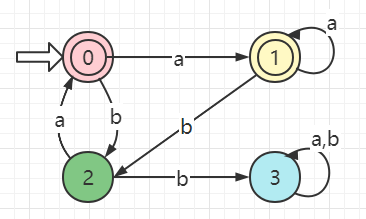
最小化
终态{0,1},非终态{2,3}
| I | Ia | Ib |
|---|---|---|
| {0,1} | {1} | {2} |
| {2,3} | {0,3} | {3} |
{0,1}包含了{1}和{2},所以不能再划分;
{0,3}不包含在{0,1}或{2,3}中,拆分由状态2经弧a到达状态0和由状态3经弧a到达状态3,即{2,3}
⟹
implies
⟹{2},{3};
得{{0,1},{2},{3}}
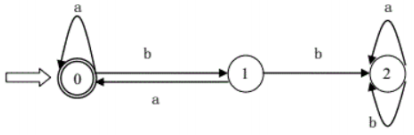
(b)已经确定化,进行最小化
终态{0,1},非终态{2,3,4,5}
| I | Ia | Ib |
|---|---|---|
| {0,1} | {1} | {2,4} |
| {2,3,4,5} | {0,1,3,5} | {2,3,4,5} |
| {2,4} | {0,1} | {3,5} |
| {3,5} | {3,5} | {2,4} |
{0,1,3,5}已经大于{0,1}了,故不继续分析
{1}和{2,4}包含于{0,1}、{2,3,4,5},故{0,1}不拆分;
{0,1,3,5}没有包含于{0,1}、{2,3,4,5};又状态24经弧a到达状态10,包含于{0,1},应拆24为一组(其他拆法可自验证),即拆分{2,3,4,5}为{2,4}、{3,5}
{{0,1},{2,4},{3,5}}
| I | Ia | Ib |
|---|---|---|
| {0,1} | {1} | {2,4} |
| {2,4} | {0,1} | {3,5} |
| {3,5} | {3,5} | {2,4} |
继续验证不可再拆,且都属于集合{{0,1},{2,4},{3,5}}。
语法分析
自上向下分析
-
消除左递归
含有左递归的文法将使自上而下的分析过程写入无限循环,如 P ⟹ + P α Poverset{+}{implies}Palpha P⟹+Pα, P ⟹ P α ⟹ P α α ⟹ P α α α ⟹ … … Pimplies Palphaimplies Palphaalphaimplies Palphaalphaalphaimplies…… P⟹Pα⟹Pαα⟹Pααα⟹……
消除左递归可以在原产生式中增加一个非终结符,如 P → P α ∣ β Prarr Palpha|beta P→Pα∣β改写为(注意 β beta β不以 P P P开头):
P → β P ′ Prarrbeta P' P→βP′
P ′ → α P ′ ∣ ε P'rarralpha P'|varepsilon P′→αP′∣ε -
消除回溯
确保对输入符号准确的指派一个候选去执行任务且此候选的工作结果是确信无疑的,避免回溯推倒重来费时费力。 -
First集和Follow集
- 令G是一个不含左递归的文法,对G的所有非终结符的每个候选
α
alpha
α定义它的终结首符集
F
I
R
S
T
(
α
)
FIRST(alpha)
FIRST(α)为:
F I R S T ( α ) = { a ∣ α ⟹ ∗ a . . . , a ∈ V T } FIRST(alpha)={a|alphaoverset{*}{implies}a...,ain V_T} FIRST(α)={a∣α⟹∗a...,a∈VT} - 假定S是文法G的开始符号,对于G的任何非终结符A,定义
F
O
L
L
O
W
(
A
)
FOLLOW(A)
FOLLOW(A):
F O L L O W ( A ) = { a ∣ S ⟹ ∗ . . . A a . . . , a ∈ V T } FOLLOW(A)={a|Soverset{*}{implies}...Aa...,a in V_T} FOLLOW(A)={a∣S⟹∗...Aa...,a∈VT}
安利DZ大佬的讲解
-
LL(1)文法
①文法不含左递归
②对于文法中每一个非终结符A的各个产生式的候选首符集两两不相交
即,若 A → α 1 ∣ α 2 ∣ . . . ∣ α n Ararralpha_1|alpha_2|...|alpha_n A→α1∣α2∣...∣αn
则 F I R S T ( α i ) ∩ F I R S T ( α j ) = Φ FIRST(alpha_i)cap FIRST(alpha_j)=varPhi FIRST(αi)∩FIRST(αj)=Φ
③对文法中的每个非终结符A,若它存在某个候选首符集合包含 ε varepsilon ε,
则 F I R S T ( A ) ∩ F O L L O W ( A ) = Φ FIRST(A)cap FOLLOW(A)=varPhi FIRST(A)∩FOLLOW(A)=Φ
文法G满足以上条件,则称G为LL(1)文法。 -
LL(1)基本思想
顾名思义,第一个L表示从左到右扫描输入串,第二个L表示最左推导,1表示分析时每一步只需向前查看一个符号。即根据输入串的当前输入符号来唯一确定选用哪个产生式来进行推导,从而消除左递归和回溯。 -
递归下降分析优缺点
| 优点 | 缺点 |
|---|---|
| 分析高效(线性时间) | 频繁递归工作效率低 |
| 错误定位和诊断信息准确 | 缺乏完善语法检查和出错处理 |
| 容易实现(方便编码) |
- LL(1)分析过程
比如如下分析表:
| i | + | |
|---|---|---|
| E | E→TE’ | |
| E’ | E’→TE’ |
太多了不想画,举一反三
初始时栈内是#E,例输入串为i,则根据表格栈顶元素E遇到i时,用TE’替代E,即逆序入栈,此时栈内为#E’T,以此类推,当输入串和栈顶都是#(结束符号)时表示成功,如果遇到分析表是空白的,则报错,如果是替换
ε
varepsilon
ε,则意味不入栈。
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
- 下面文法中,那些是LL(1)的,说明理由。
(1)
S
→
A
b
c
Srarr Abc
S→Abc
A
→
a
∣
ε
Ararr a|varepsilon
A→a∣ε
B
→
b
∣
ε
Brarr b|varepsilon
B→b∣ε
| FIRST | FOLLOW | |
|---|---|---|
| S | {a,b} | {#} |
| A | {a, ε varepsilon ε} | {b} |
| b | {b, ε varepsilon ε} | Φ varPhi Φ |
是,满足三个条件
(2)
S
→
A
b
Srarr Ab
S→Ab
A
→
a
∣
B
∣
ε
Ararr a|B|varepsilon
A→a∣B∣ε
B
→
b
∣
ε
Brarr b|varepsilon
B→b∣ε
| FIRST | FOLLOW | |
|---|---|---|
| S | {a,b} | {#} |
| A | {a,b, ε varepsilon ε} | {b} |
| B | {b, ε varepsilon ε} | {b} |
FIRST(A)
∩
cap
∩FOLLOW(A)={b}
FIRST(B)
∩
cap
∩FOLLOW(B)={b}
不是,A、B不满足条件③
(3)
S
→
A
B
B
A
Srarr ABBA
S→ABBA
A
→
a
∣
ε
Ararr a|varepsilon
A→a∣ε
B
→
b
∣
ε
Brarr b|varepsilon
B→b∣ε
| FIRST | FOLLOW | |
|---|---|---|
| S | {a,b, ε varepsilon ε} | {#} |
| A | {a, ε varepsilon ε} | {#,a,b} |
| B | {b, ε varepsilon ε} | {#,a,b} |
FIRST(A)
∩
cap
∩FOLLOW(A)={a}
FIRST(B)
∩
cap
∩FOLLOW(B)={b}
不是,A、B不满足条件③
(4)
S
→
a
S
e
∣
B
Srarr aSe|B
S→aSe∣B
B
→
b
B
e
∣
C
Brarr bBe|C
B→bBe∣C
C
→
c
C
e
∣
d
Crarr cCe|d
C→cCe∣d
| FIRST | FOLLOW | |
|---|---|---|
| S | {a,b,c,d} | {#,e} |
| B | {b,c,d} | {#,e} |
| C | {c,d} | {#,e} |
FIRST(aSe)
∩
cap
∩FIRST(B)=
Φ
varPhi
Φ
FIRST(bBe)
∩
cap
∩FIRST(C )=
Φ
varPhi
Φ
FIRST(cCe)
∩
cap
∩FIRST(d)=
Φ
varPhi
Φ
是,满足三个条件
其实没有
ε
varepsilon
ε可以不用求FOLLOW集。
自下向上分析
-
短语、直接短语、句柄
令 G G G是一个文法, S S S是文法的开始符号,假定 α β δ alphabetadelta αβδ是文法 G G G的一个句型,如果有
S ⟹ ∗ α A δ Soverset{*}{implies}alpha Adelta S⟹∗αAδ且 A ⟹ + β Aoverset{+}{implies}beta A⟹+β
则称 β beta β是句型 α β δ alphabetadelta αβδ相对于非终结符A的短语。特别是,如果有
A → β Ararrbeta A→β
则称 β beta β是句型 α β δ alphabetadelta αβδ相对于规则 A → β Ararrbeta A→β的直接短语,一个句型的最左直接短语称为该句型的句柄。 -
规范规约、规范推导
假定 α alpha α是文法 G G G的一个句子,我们称序列 α n , α n − 1 . . . , a 0 alpha_n,alpha_{n-1}...,a_0 αn,αn−1...,a0是 α alpha α的一个规范规约,如果此序列满足:
① α n = α alpha_n=alpha αn=α
② α 0 alpha_0 α0为文法的开始符,即 α 0 = S alpha_0=S α0=S
③对任何 i , 0 < i ≤ n , α i − 1 i,0<i≤n,alpha_{i-1} i,0<i≤n,αi−1是从 α i alpha_i αi经把句柄替换为相应产生式的左部符号而得到的。
规范规约是关于 α alpha α的一个最右推导的逆过程,故规范规约也称最左规约。
在形式语言中,最右推导常被称为规范推导,由规范推导所得的句型称为规范句型。 -
前缀、活前缀
字的前缀是指该字的任意首部。例如字abc的前缀有ε、a、ab或abc。所谓活前缀是指规范句型的一个前缀,这种前缀不含句柄之后的任何符号。之所以称为活前缀,是因为在右边增添一些终结符号之后,就可以使它成为一个规范句型。
在LR分析工作过程中的任何时候,栈里的文法符号(自栈底而上)X1X2…Xm应该构成活前缀,把输入串的剩余部分配上之后即应成为规范句型(如果整个输入串确实构成一个句子)。因此只要输入串的已扫描部分保持可归约成一个活前缀,那就意味着所扫描过的部分没有错误。 -
LR分析基本思想
在规约过程中,一方面记住已移进和规约出的整个符号串,即记住“历史”;
另一方面根据所用的产生式推测未来可能遇到的输入符号,即对未来进行“展望”;
最后结合“现实”的输入符号来确定栈顶符号串是否构成相对某一产生式的句柄。 -
有效项目
我们说项目 A → β 1 ⋅ β 2 Ararrbeta_1·beta_2 A→β1⋅β2对活前缀 α β 1 alphabeta_1 αβ1有效的,其条件是存在规范推导:
S ′ ⟹ R ∗ α A w ⟹ R α β 1 β 2 w S'overset{*}{underset{R}{implies}}alpha Awunderset{R}{implies}alphabeta_1beta_2w S′R⟹∗αAwR⟹αβ1β2w -
LR(1)分析过程
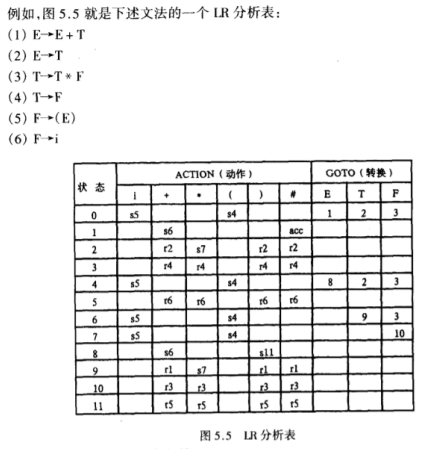
(1)sj 把下一状态j和现行输入符号a移进栈;
(2) rj 按第j个产生式进行归约;
(3)acc 接受;
(4)空白格 出错标志,报错
利用图5.5 分析表,假定输人串为 i ∗ i + i i*i+i i∗i+i,LR分析器的工作过程(即,三元式的变化过程)如下:

- 第(1)步到第(2)步:状态0,输入i,定位表格[0,i]=s5,入栈状态5和输入i,输入串出栈;
- 第(2)步到第(3)步:栈顶状态5,输入*,定位[5,*]=r6,用第6个产生式F→i规约,出栈5和i,入栈F,此时看GOTO,栈顶状态0,定位[0,F],入栈状态3;
- 第(3)步到第(4)步:定位[3,*]=r4,用第4个产生式T→F规约,出栈3和F,入栈T,此时GOTO[0,T]=2,入栈状态2;
- 第(3)步到第(4)步:定位[2,*]=s7,入栈状态7和输出*,输入串出栈;
- 以此类推,不一一写了。
- LR(0)分析过程:
考虑文法
S → A S ∣ b Srarr AS|b S→AS∣b
A → S A ∣ a Ararr SA|a A→SA∣a
(1)列出这个文法的所有LR(0)项目。
0 S ′ → ⋅ S S'rarr·S S′→⋅S
1 S ′ → S ⋅ S'rarr S· S′→S⋅
2 S → ⋅ A S Srarr ·AS S→⋅AS
3 S → A ⋅ S Srarr A·S S→A⋅S
4 S → A S ⋅ Srarr AS· S→AS⋅
5 S → ⋅ b Srarr ·b S→⋅b
6 S → b ⋅ Srarr b· S→b⋅
7 A → ⋅ S A Ararr ·SA A→⋅SA
8 A → S ⋅ A Ararr S·A A→S⋅A
9 A → S A ⋅ Ararr SA· A→SA⋅
10 A → ⋅ a Ararr ·a A→⋅a
11 A → a ⋅ Ararr a· A→a⋅
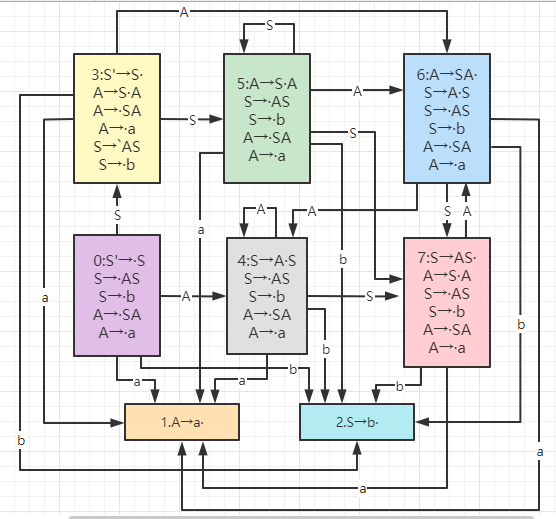
(2)构造这个文法的LR(0)项目集规范族及识别活前缀的DFA。
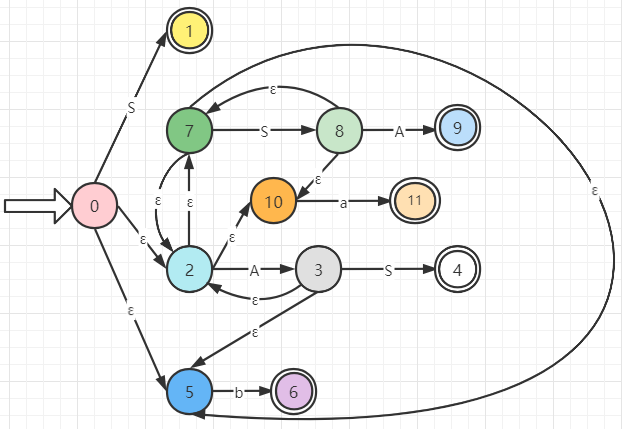
确定化
| S | A | a | b | |
|---|---|---|---|---|
| {0,2,5,7,10} | {1,2,5,7,8,10} | {2,3,5,7,10} | {11} | {6} |
| {1,2,5,7,8,10} | {2,5,7,8,10} | {2,3,5,7,9,10} | {11} | {6} |
| {2,3,5,7,9,10} | {2,4,5,7,8,10} | {2,3,5,7,10} | {11} | {6} |
| {2,4,5,7,8,10} | {2,5,7,8,10} | {2,3,5,7,9,10} | {11} | {6} |
| {11} | Φ varPhi Φ | Φ varPhi Φ | Φ varPhi Φ | Φ varPhi Φ |
| {6} | Φ varPhi Φ | Φ varPhi Φ | Φ varPhi Φ | Φ varPhi Φ |
I
0
=
S
′
→
⋅
S
,
S
→
⋅
A
S
,
S
→
⋅
b
.
A
→
⋅
S
A
,
A
→
⋅
a
I_0={S'rarr·S,Srarr·AS,Srarr·b.Ararr·SA,Ararr·a}
I0=S′→⋅S,S→⋅AS,S→⋅b.A→⋅SA,A→⋅a
G
O
(
I
0
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_0,a)={Ararr a·}=I_1
GO(I0,a)={A→a⋅}=I1
G
O
(
I
0
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_0,b)={Srarr b·}=I_2
GO(I0,b)={S→b⋅}=I2
G
O
(
I
0
,
S
)
=
{
S
′
→
S
⋅
,
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
a
⋅
}
=
I
3
GO(I_0,S)={S'rarr S·,Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr a·}=I_3
GO(I0,S)={S′→S⋅,A→S⋅A,S→⋅AS,S→⋅b,A→⋅SA,A→ a⋅}=I3
G
O
(
I
0
,
A
)
=
{
S
→
A
⋅
S
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
4
GO(I_0,A)={Srarr A·S,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_4
GO(I0,A)={S→A⋅S,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I4
G
O
(
I
3
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_3,a)={Ararr a·}=I_1
GO(I3,a)={A→a⋅}=I1
G
O
(
I
3
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_3,b)={Srarr b·}=I_2
GO(I3,b)={S→b⋅}=I2
G
O
(
I
3
,
S
)
=
{
A
→
S
⋅
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
5
GO(I_3,S)={Ararr S·,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_5
GO(I3,S)={A→S⋅,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I5
G
O
(
I
3
,
A
)
=
{
A
→
S
A
⋅
,
S
→
A
⋅
S
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
6
GO(I_3,A)={Ararr SA·,Srarr A·S,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_6
GO(I3,A)={A→SA⋅,S→A⋅S,S→⋅AS,S→ ⋅b,A→⋅SA,A→⋅a}=I6
G
O
(
I
4
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_4,a)={Ararr a·}=I_1
GO(I4,a)={A→a⋅}=I1
G
O
(
I
4
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_4,b)={Srarr b·}=I_2
GO(I4,b)={S→b⋅}=I2
G
O
(
I
4
,
S
)
=
{
S
→
A
S
⋅
,
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
7
GO(I_4,S)={Srarr AS·,Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_7
GO(I4,S)={S→AS⋅,A→S⋅A,S→⋅AS,S→ ⋅b,A→⋅SA,A→⋅a}=I7
G
O
(
I
4
,
A
)
=
{
S
→
A
⋅
S
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
4
GO(I_4,A)={Srarr A·S,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_4
GO(I4,A)={S→A⋅S,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I4
G
O
(
I
5
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_5,a)={Ararr a·}=I_1
GO(I5,a)={A→a⋅}=I1
G
O
(
I
5
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_5,b)={Srarr b·}=I_2
GO(I5,b)={S→b⋅}=I2
G
O
(
I
5
,
S
)
=
{
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
5
GO(I_5,S)={Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_5
GO(I5,S)={A→S⋅A,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I5
G
O
(
I
5
,
A
)
=
{
A
→
S
A
⋅
,
S
→
A
⋅
S
,
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
6
GO(I_5,A)={Ararr SA·,Srarr A·S,Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_6
GO(I5,A)={A→SA⋅,S→A⋅S,A→S⋅A,S→⋅AS,S→ ⋅b,A→⋅SA,A→⋅a}=I6
G
O
(
I
6
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_6,a)={Ararr a·}=I_1
GO(I6,a)={A→a⋅}=I1
G
O
(
I
6
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_6,b)={Srarr b·}=I_2
GO(I6,b)={S→b⋅}=I2
G
O
(
I
6
,
S
)
=
{
S
→
A
S
⋅
,
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
7
GO(I_6,S)={Srarr AS·,Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_7
GO(I6,S)={S→AS⋅,A→S⋅A,S→⋅AS,S→ ⋅b,A→⋅SA,A→⋅a}=I7
G
O
(
I
6
,
A
)
=
{
S
→
A
⋅
S
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
4
GO(I_6,A)={Srarr A·S,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_4
GO(I6,A)={S→A⋅S,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I4
G
O
(
I
7
,
a
)
=
{
A
→
a
⋅
}
=
I
1
GO(I_7,a)={Ararr a·}=I_1
GO(I7,a)={A→a⋅}=I1
G
O
(
I
7
,
b
)
=
{
S
→
b
⋅
}
=
I
2
GO(I_7,b)={Srarr b·}=I_2
GO(I7,b)={S→b⋅}=I2
G
O
(
I
7
,
S
)
=
{
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
5
GO(I_7,S)={Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_5
GO(I7,S)={A→S⋅A,S→⋅AS,S→⋅b,A→ ⋅SA,A→⋅a}=I5
G
O
(
I
7
,
A
)
=
{
A
→
S
A
⋅
,
S
→
A
⋅
S
,
A
→
S
⋅
A
,
S
→
⋅
A
S
,
S
→
⋅
b
,
A
→
⋅
S
A
,
A
→
⋅
a
}
=
I
6
GO(I_7,A)={Ararr SA·,Srarr A·S,Ararr S·A,Srarr ·AS,Srarr ·b,Ararr ·SA,Ararr ·a}=I_6
GO(I7,A)={A→SA⋅,S→A⋅S,A→S⋅A,S→⋅AS,S→ ⋅b,A→⋅SA,A→⋅a}=I6
项目集规范族为 C = { I 0 , I 1 , I 2 , I 3 , I 4 , I 5 , I 6 , I 7 } C={I_0,I_1,I_2,I_3,I_4,I_5,I_6,I_7} C={I0,I1,I2,I3,I4,I5,I6,I7}
属性文法
属性文法、综合属性、继承属性
属性文法(也称属性翻译文法)是在上下文无关文法的基础上为每个文法符号(终结符或非终结符)配备若干相关的“值"(称为属性)。.
这些属性代表与文法符号相关信息,例如它的类型、值、代码序列、符号表内容等等。属性与变量一样,可以进行计算和传递。属性加工的过程即是语义处理的过程。对于文法的每个产生式都配备了一组属性的计算规则,称为语义规则。
综合属性:自下而上传递信息
继承属性:自上而下传递信息
要特别强调的是:
- 终结符只有综合属性,它们由词法分析器提供;
- 非终结符既可有综合属性也可有继承属性,文法开始符号的所有继承属性作为属性计算前的初始值。
语义分析和是中间代码产生
中间代码生成对编译器构造的意义
- 便于进行与机器无关的代码优化工作;
- 使编译程序改变目标机更容易;
- 使编译程序的结构在逻辑上更为简单明确。以中间语言为界面,编译前端和后端的接口更清晰。
优化
代码优化的原则
- 等价原则:经过优化后不应改变程序运行的结果。
- 有效原则:使优化后所产生的目标代码运行时间较短,占用的存储空间较小。
- 合算原则:应尽可能以较低的代价取得较好的优化效果。
目标代码生成
代码生成器的输出是目标程序,目标程序有哪几种形式?
- 能够立即执行的机器语言代码,所有地址均已定位(代真)。
- 待装配的机器语言模块。当需要执行时,由连接装入程序把它们和某些运行程序连接起来,转换成能执行的机器语言代码。
- 汇编语言代码,尚需经过汇编程序汇编,转换成可执行的机器语言代码。
参考文献
《程序设计语言编译原理(第3版)》-陈火旺等著
原创不易,请勿转载(
本不富裕的访问量雪上加霜)
博主首页:https://wzlodq.blog.csdn.net/
来都来了,不评论两句吗????
如果文章对你有帮助,记得一键三连❤
最后
以上就是仁爱美女最近收集整理的关于编译原理复习总结-耗子尾汁引论语法描述词法分析语法分析属性文法语义分析和是中间代码产生优化目标代码生成的全部内容,更多相关编译原理复习总结-耗子尾汁引论语法描述词法分析语法分析属性文法语义分析和是中间代码产生优化目标代码生成内容请搜索靠谱客的其他文章。








发表评论 取消回复