前馈神经网络的简单实现

60 阅读 0 评论 40 点赞

我是靠谱客的博主高高冬日，最近开发中收集的这篇文章主要介绍前馈神经网络的简单实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

神经网络是机器学习的一个重要方法，就像人类学习的本质是建立神经元之间的联系一样，机器学习也可以模拟相应的“神经元”并建立这些“神经元”之间的联系，人的认知可以看做是神经网络的训练，如识别图片，大脑一旦认识了某张图片，那么同一张图片不管是经过旋转还是伸缩，大脑依然可以识别出来。回到机器学习领域，如果我们用了足够多的“神经元”，多到可以与人的大脑相媲美，那么我们就可以憧憬将机器训练得跟人类的大脑一样强大。机器学习中的神经网络结构大致如下图所示：

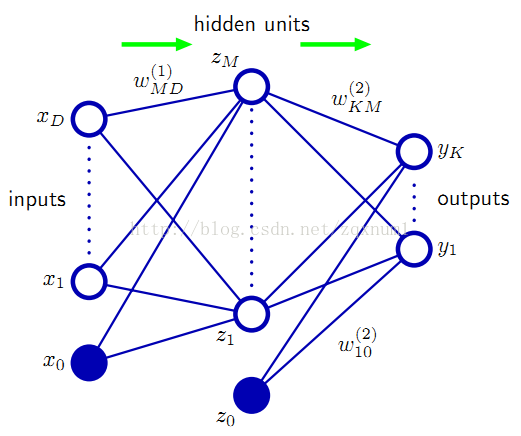
图中的圆圈就是所谓的“神经元”，也叫节点（Unit），其中用Z标注的又叫做隐藏节点（Hidden Unit），X是输入这个神经网络的东西，可以理解为我们眼睛看见的东西，Y是神经网络的输出，可以理解为大脑的认知结果。中间的隐藏节点可以看做是对输入信息的提炼，例如当输入一张图片时，我们可以将图片分解成了一块一块的区域（Z1，Z2，......），每个区域有各自的颜色、亮度，这些颜色亮度就是隐藏节点Z1、Z2的值。如果还有第二层的隐藏节点，我们可以对这些信息做进一步的提炼，这样经过层层提炼后，我们就拿到了最能反映这张图片本质的元素，所以即使日后同一张图片经过旋转或伸缩后进入我们的神经网络，我们都可以将它正确识别出来。上面的识别过程可以看做是信息从输入（X）一直向前流到了输出（Y），所以这个网络也叫前馈神经网络。

婴儿的大脑就像一个没有经过训练的神经网络，孩子在后天的学习过程就是神经网络的训练过程，经过学习，它才知道什么是猫，猫有四条腿等等。我们就拿猫的例子来说明神经网络的训练，比如孩子看到一只猫，他就看到了它的体型（Z1）、颜色（Z2）等，然后家长告诉他这是一只猫，之后孩子又看到另外一只猫，发现体型与之前的差不多，但毛发的颜色不太一样，但是家长告诉他这也是只猫，所以在孩子的认知里就会觉得体型更能决定一个动物是不是猫。这反映在神经网络中就是Z1的权重W1会增大，而Z2的权重W2会减小，当我们把所有这些W都训练好时，这个神经网络就可以正确工作了。

神经网络的数学模型

从神经网络的结构上可以看到，我们的Z是对X计算得到的，而Y又是对Z计算得到的，在计算Y时，Z的角色与在计算Z时X的角色相同，所以这个神经网络可以看做是两层（two-layer）神经网络，我们只对其中一层进行建模即可，这里我们统一将一层的输入计为X，将该层的输出计为Y，那么Y和X的关系可以用如下数学表达式表达：

w就是权重，w j*xj就是根据权重来取舍信息，f一般用Sigmod函数，就是对经过取舍后的信息做个运算，有点做是非判断的意思。详细的说明可以参考《Pattern Recognition and Machine Learning》。训练的过程就是寻找最合适的w的过程，寻找的准则就是误差最小：

这里的tn就是x在真实世界里对应的结果，y就是神经网络输出的结果，最理想的就是这两个结果是相同的，但难免会有误差，我们的目标就是寻找合适的w，让这个误差最小。譬如输入的图片是只猫，某个w使得神经网络的识别结果是鸟，这个误差就比较大了，但是如果神经网络的输出结果是虎，这个误差就相对小很多。从数学上面看，最直接的方法就是E(w)对w求导，导数为0的地方就是我们要找的w，就像开口朝上的二次函数的最低点（E(w)有点像w的二次函数）。但实际中常常使用的迭代的方法一步一步地去寻找最优的w，如梯度下降法：

每得到一个w，我们就可以把它带到E(w)中，看E(w)是否小于某个值，当E(w)足够小时，我们就认为找到了最合适的w。如何计算梯度呢？数学上可以通过求导来得到，但实际中我们求助于另一个算法：Error Backpropagation。关于这个算法的原理同样可以参考上面那本书（太多符号了我这儿就偷个懒）。

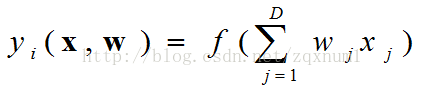
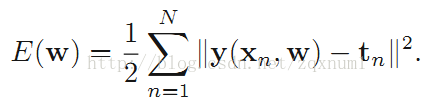
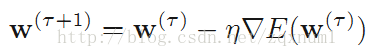
神经网络的代码实现

在下面这份代码中，神经网络的层数可以自己设定，同时也可以设定每一层的节点数（42行），代码的主要写法是递归，主要定义了两个函数，forward()和backward()，前者用于从X求Y，后者用于求梯度。

import numpy as np
from scipy.misc import derivative
import matplotlib.pylab as plt

def identy(x):
    return x

def forward(xin,connt,actfc):
    
    x_d1,x_d2 = xin.  shape
    c_d1,c_d2 = connt.shape
    assert x_d1+1==c_d1
    
    zin = np.vstack((xin,np.ones((1,x_d2))))
    a = np.array(np.mat(connt).T * np.mat(zin))
    z = actfc(a)

    return a,z

def backward(dtin,ain,zin,connt,actfc):
    d_d1,d_d2 = dtin.shape
    a_d1,a_d2 = ain.shape
    z_d1,z_d2 = zin.shape
    c_d1,c_d2 = connt.shape
    assert (d_d1==c_d2) & (a_d1==z_d1==c_d1-1)
    
    dt = np.array(np.mat(connt[0:c_d1-1,:]) * np.mat(dtin))
    dt = derivative(actfc,ain,order=5)*dt

    z = np.vstack((zin,np.ones((1,z_d2))))

    e = np.zeros((c_d1,c_d2))
    for i in range(0,c_d1):
        e[i] = np.sum(z[i]*dtin,axis=1)/d_d2
    ##print(e.shape)
    return e,dt
        

x = np.array([np.linspace(-7, 7, 200)])
t = np.cos(x) * 0.5

units = np.array([1,8,5,3,1])
units_bias = units+1
##print(units_bias)

connt = {}
for i in range(1,len(units_bias)):
    connt[i] = np.random.uniform(-1,1,size=(units_bias[i-1],units[i]))
##print(connt)

actfc = {0:identy}
for i in range(1,len(units_bias)-1):
    actfc[i] = np.tanh
actfc[len(units)-1] = identy
##print(actfc)
    
for k  in range(0,5000):
    a = {0:x}
    z = {0:actfc[0](a[0])}
    for i in range(1,len(units)):
        a[i],z[i] = forward(z[i-1],connt[i],actfc[i])

    dt = {len(units)-1:z[i]-t}
    e = {}
    for i in range(len(units)-1,0,-1):
        e[i],dt[i-1] = backward(dt[i],a[i-1],z[i-1],connt[i],np.tanh)

    pp = 0.05
    for i in range(1,len(units_bias)):
        connt[i] = connt[i]-pp*e[i]
    ##print(connt)

a = {0:x}
z = {0:actfc[0](a[0])}
for i in range(1,len(units)):
    a[i],z[i] = forward(z[i-1],connt[i],actfc[i])

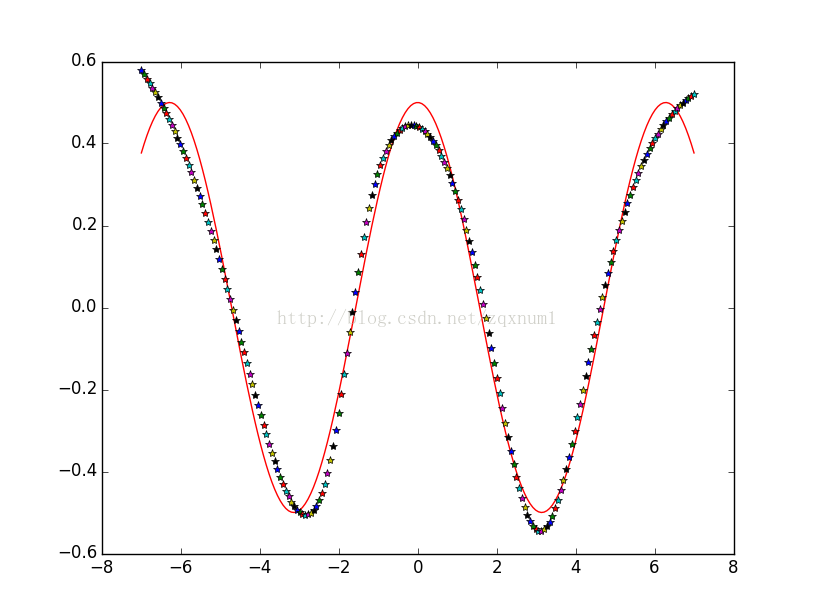
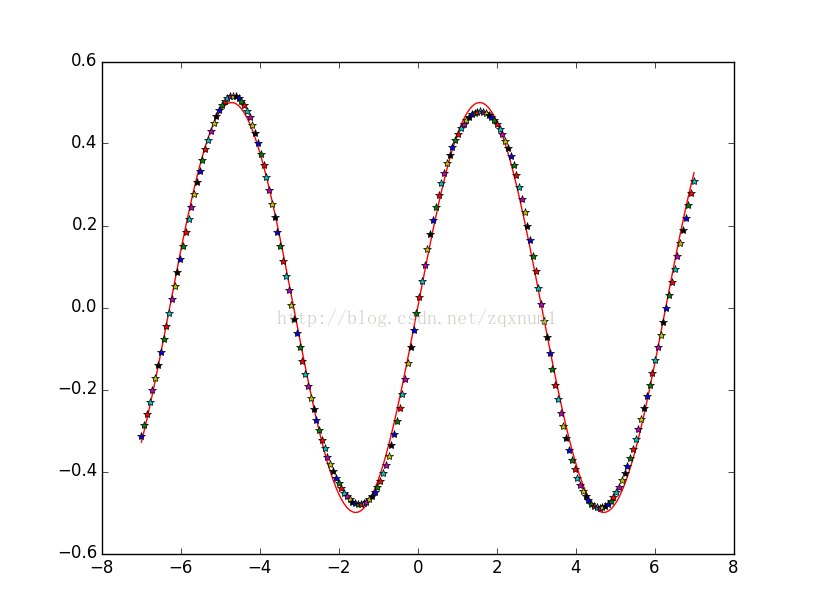
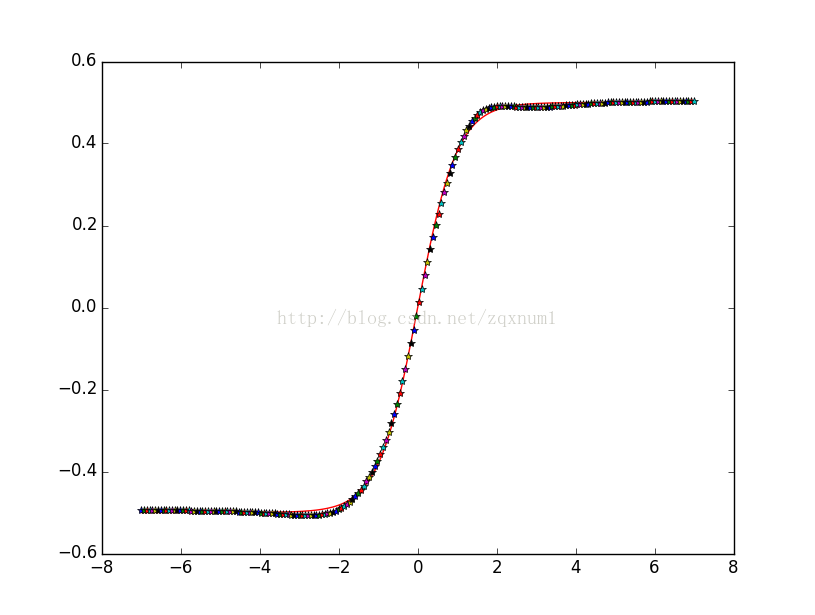
plt.plot(x.T,t.T,'r',x,a[len(units)-1],'*')
plt.show()

我们从余弦函数中生成一些数据，然后用这些数据区训练神经网络，可以看到神经网络的输出能很好地拟合正弦函数：