关于反向传播是否更新偏置b的探索 2.0

​
问题是怎么产生的：

在研究神经网络反向传播过程中发现很多资料的参数更新过程都只分析了参数w的更新，而作为参数的b到底更不更新呢？

模拟的神经网络如下：

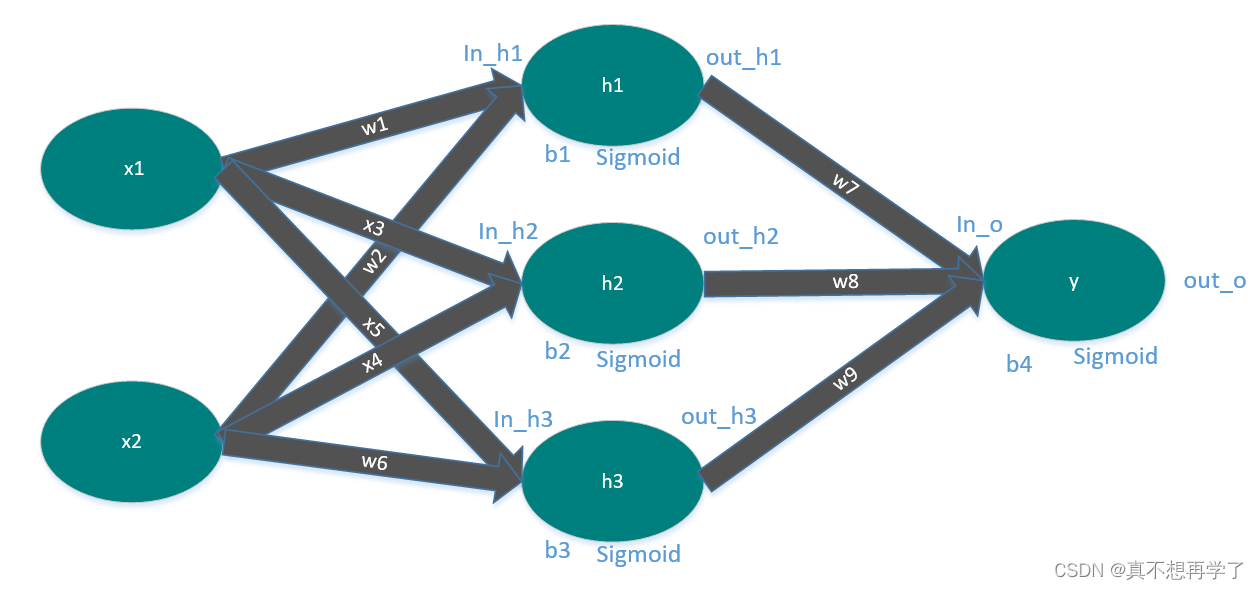
源代码：

#coding:utf-8

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a

def forward_propagate(x1, x2, w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4):
    '''传入输入和参数'''
    '''隐藏层'''
    in_h1 = w1 * x1 + w2 * x2+b1
    out_h1 = sigmoid(in_h1)
    in_h2 = w3 * x1 + w4 * x2+b2
    out_h2 = sigmoid(in_h2)
    in_h3 = w5 * x1 + w6 * x2 + b3
    out_h3 = sigmoid(in_h3)
    '''输出层'''
    in_o =w7*out_h1+ w8 * out_h2 + w9 * out_h3+b4
    out_o = sigmoid(in_o)
    '''输出隐藏层输出和输出层输出'''
    return out_o, out_h1, out_h2,out_h3


def back_propagate(out_o,out_h1, out_h2,out_h3):
    '''传入隐藏层出和输出层输出'''
    # 反向传播
    '''计算均方误差的第一层偏导'''
    '''(y-y')'''
    d_o= out_o - y
    '''计算误差对参数w7、w8、w9的偏导数'''
    '''d_w7=(y-y')*y*(1-y)*h_1'''
    d_w7 = d_o * out_o * (1 - out_o) * out_h1
    d_w8 = d_o * out_o * (1 - out_o) * out_h2
    d_w9 = d_o * out_o * (1 - out_o) * out_h3
    '''计算误差对参数w1,w2的偏导数'''
    '''d_w1=(y-y')*y*(1-y)*w_7*h_1*(1-h_1)*x_1'''
    d_w1=d_w7*w7*(1-out_h1)*x1
    d_w2 =d_w7*w7*(1-out_h1)*x2
    '''计算误差对参数w3,w4的偏导数'''
    '''d_w3=(y-y')*y*(1-y)*w_8*h_2*(1-h_2)*x_1'''
    d_w3 = d_w8 * w8 * (1 - out_h2) * x1
    d_w4 = d_w8 * w8 * (1 - out_h2) * x2
    '''计算误差对参数w5,w6的偏导数'''
    '''d_w5=(y-y')*y*(1-y)*w_9*h_3*(1-h_3)*x_1'''
    d_w5 = d_w9 * w9* (1 - out_h3) * x1
    d_w6= d_w9 * w9 * (1 - out_h3) * x2
    '''计算误差对参数b4的偏导数'''
    '''d_b4=(y-y')*y*(1-y)*1'''
    d_b4=d_o*out_o*(1-out_o)
    '''计算误差对参数b1,b2,b3的偏导数'''
    '''d_b1=(y-y')*y*(1-y)*w_7*h_1*(1-h_1)*1'''
    d_b1=d_b4*w7*out_h1*(1-out_h1)
    d_b2 = d_b4 * w8 * out_h2 * (1 - out_h2)
    d_b3 = d_b4 * w9 * out_h3 * (1 - out_h3)
    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8,d_w9,d_b1,d_b2,d_b3,d_b4


def update_b(w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4,lr=0.01):
    # 步长
    step =lr
    b1 = b1 - step * d_b1
    b2 = b2 - step * d_b2
    b3 = b3 - step * d_b3
    b4 = b4 - step * d_b4
    return w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4

def update_w(w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4,lr=0.01):
    # 步长
    step =lr
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    w9 = w9 - step * d_w9
    return w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4

def update_w_b(w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4,lr=0.01):
    # 步长
    step =lr
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    w9 = w9 - step * d_w9
    b1 = b1 - step * d_b1
    b2 = b2 - step * d_b2
    b3 = b3 - step * d_b3
    b4 = b4 - step * d_b4
    return w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4

if __name__ == "__main__":
    plt.figure()
    epoches=3000
    labels=['only update w','only update b','update w and b']
    for j,updatefunc in enumerate([update_w,update_b,update_w_b]):
        w1, w2, w3, w4, w5, w6, w7, w8, w9 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8, 0.1
        b1, b2, b3, b4 = 0.1, 0.21, 0.11, 0.22
        x1, x2 = 0.5, 0.3
        y = 0.09
        print("=====输入值：x1, x2；真实输出值：y=====")
        print(x1, x2, y)
        print("=====更新前的权值=====")
        print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
              round(w8, 2), round(w9, 2), round(b1, 2), round(b2, 2), round(b3, 2), round(b4, 2))
        loss = []
        for i in range(epoches):
            out_o, out_h1, out_h2,out_h3 = forward_propagate(x1, x2, w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4)
            d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8,d_w9 ,d_b1,d_b2,d_b3,d_b4= back_propagate(out_o,  out_h1, out_h2,out_h3)
            w1, w2, w3, w4, w5, w6, w7, w8 ,w9,b1,b2,b3,b4= updatefunc(w1, w2, w3, w4, w5, w6, w7, w8,w9,b1,b2,b3,b4,lr=0.01)
            error = (1 / 2) * (out_o - y) ** 2
            loss.append(error)
            if i%100==0:
                print("正向计算：o")
                print(round(out_o, 5))
                print("=====第" + str(i) + "轮=====")
                print("损失函数：均方误差")
                print(round(error, 5))
                print("反向传播：误差传给每个权值")
                print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
                      round(d_w7, 5), round(d_w8, 5), round(d_w9, 5),round(d_b1, 2), round(d_b2, 2), round(d_b3, 2), round(d_b4, 2))

        print("更新后的权值")
        print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
              round(w8, 2),round(w9, 2),round(b1, 2), round(b2, 2), round(b3, 2), round(b4, 2))

        x=range(epoches)
        plt.plot(x,loss,label=labels[j])
    plt.legend()
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.show()

运行结果：

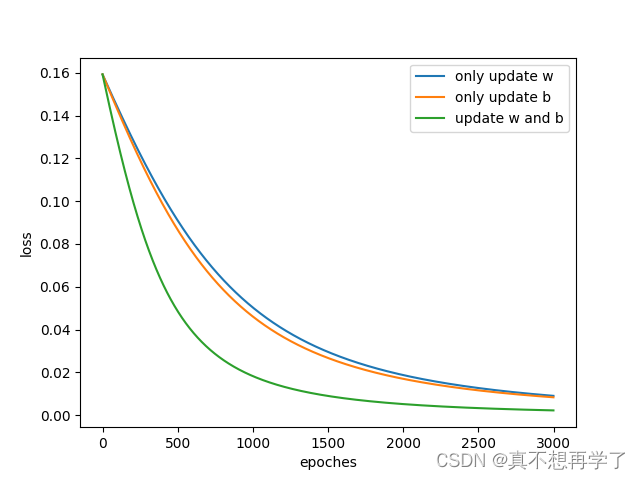
结论：
1.更新偏置b可以加速模型的拟合，这也验证了，模型越复杂，拟合的就越快。
2,只更新偏置数b也可以实现模型的拟合，而且效果不错，在本次实验中甚至比只更新w效果还要好。

其他：
偏置的作用：
1.功能上：偏置可以加速神经网络拟合。
加了偏置项的神经网络有更复杂的参数结构，拟合能力更好。
2.形式上：偏置b可以视为控制每个神经元的阈值（-b等于神经元阈值）。
举例如：神经元的激活函数f为sign。每个神经元的输出即为sign(WX +b)。
当 wx < -b时， 输出值为-1，也就是抑制。
当 wx >= -b时， 输出值为1也就是激活。

关于为什么是2.0:
1.0的代码出了点问题，损失对参数b求导的代码编错了，（计算的公式是没错的，但是代码编错了，就错了一点点），导致实验结果即结论都出了问题。琢磨了好几天，想来想去关于偏置b的作用和上次的实验。最终检查代码实现时发现了错误，真是差之毫厘，谬以千里。

ref：
https://blog.csdn.net/mmww1994/article/details/81705991
https://www.cnblogs.com/h694879357/p/16590346.html
​

最后

以上就是跳跃蚂蚁为你收集整理的关于反向传播是否更新偏置b的探索 2.0的全部内容，希望文章能够帮你解决关于反向传播是否更新偏置b的探索 2.0所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。