RNN代码实现

1.引言

在图像处理中，目前做的最好的是CNN
自然语言处理中，表现比较好的是RNN
既然我们已经有了人工神经网络和卷积神经网络，为什么还要循环神经网络？
原因很简单，无论是卷积神经网络，还是人工神经网络，他们的前提假设都是：元素之间是相互独立的，输入与输出也是独立的
循环神经网络，他的本质是：像人一样拥有记忆的能力。因此，他的输出就依赖于当前的输入和记忆。

2.RNN结构：

RNN中的结构细节：

1.可以把$s_t$当作隐状态，捕捉了之前时间点上的信息。
2.$o_t$是由当前时间以及之前所有的记忆得到的。就是你考研之后做的考试卷子，是用你的记忆得到的。
3.很可惜的是，$s_t$并不能捕捉之前所有时间点的信息。就像你考研不能记住所有的英语单词一样。
4.和卷积神经网络一样，这里的网络中每个 cell 都共享了一组参数（U，V，W）,这样就能极大的降低计算量了。
5.$o_t$在很多情况下都是不存在的，因为很多任务，比如文本情感分析，都是只关注最后的结果的。
请添加图片描述

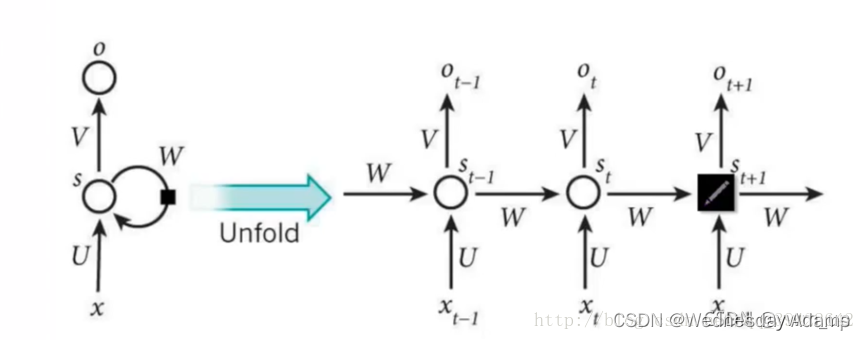
用一句话解释RNN，就是一个单元结构重复使用。
定义：
$x_t$: 表示t时刻的输入
$o_t$: 表示t时刻的输出
$s_t$: 表示t时刻的记忆
当前时刻的输出是由：以前的记忆和当前时刻的输入决定的，神经网络最擅长做的就是通过一系列参数把很多内容整合到一起，然后学习这个参数，因此就定义了RNN的基础：

• σ()是神经网络中的激活函数
• 套用一个激活函数，可以用来做一个非线性映射，也可以用来过滤信息

2.代码实现二进制相加

我们现在使用循环神经网络去建模二进制加法。你看到下面的序列了么？上边这俩在方框里的，有颜色的1是什么意思呢？

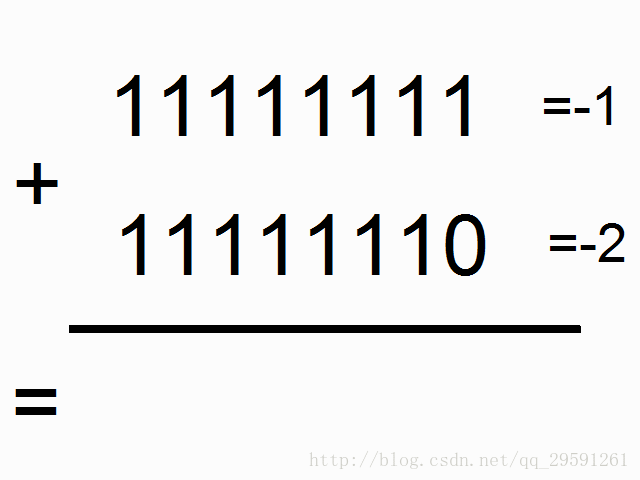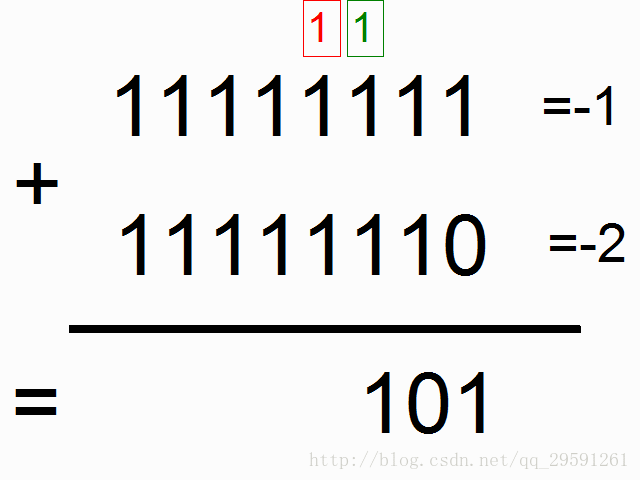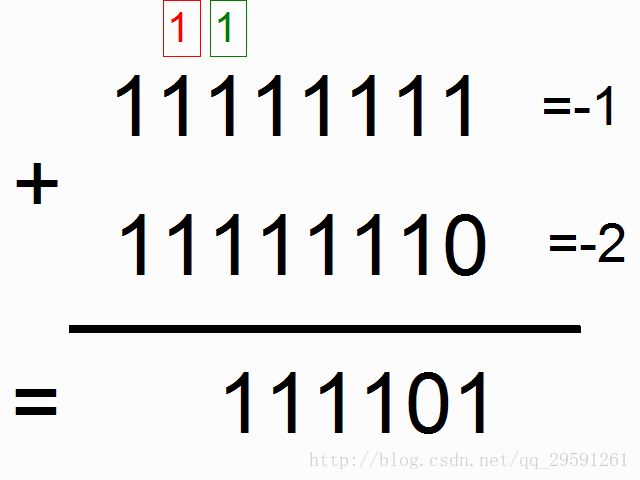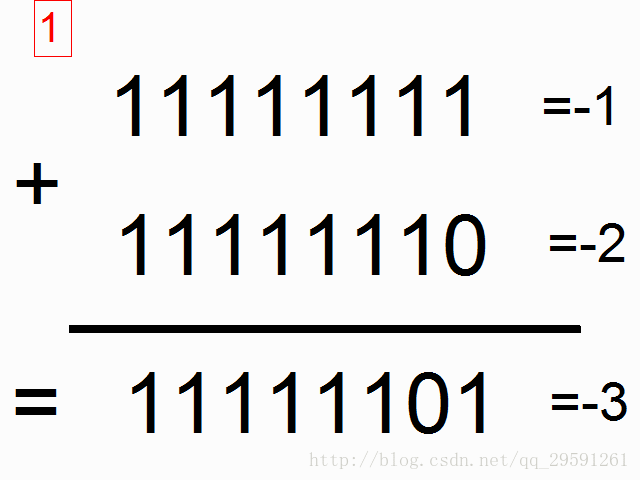
框框中彩色的1表示“携带位”。当每个位置的和溢出时（需要进位），它们“携带这个‘1’”。我们就是要教神经网络学习去记住这个“携带位”。当“和”需要它，它需要去“携带这个‘1’”。

二进制加法从右边到左边进行计算，我们试图通过上边的数字，去预测横线下边的数字。我们想让神经网络遍历这个二进制序列并且记住它携带这个1与没有携带这个1的时候，这样的话网络就能进行正确的预测了。不要迷恋于这个问题本身，因为神经网络事实上也不在乎。就当作我们有两个在每个时间步数上的输入（1或者0加到每个数字的开头），这两个输入将会传播到隐含层，隐含层会记住是否有携带位。预测值会考虑所有的信息，然后去预测每个位置（时间步数）正确的值。
完整代码：

import numpy as np

# sigmoid
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

# sigmoid导数
def sigmoid_derivative(output):
    return output * (1.0 - output)

# 生成整数与二进制数转化字典
int2binary = {}
binary_dim = 8

largest_number = pow(2, binary_dim)
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T,
                       axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]

# 模型参数
input_dim = 2
hidden_dim = 16
output_dim = 1
learing_rate = 1e-1

# 初始化模型参数
# 模型: h(t) = sigmoid(Ux + Wh(t-1)) -> output(t) = sigmoid(Vh(t))
U = np.random.randn(input_dim, hidden_dim)
W = np.random.randn(hidden_dim, hidden_dim)
V = np.random.randn(hidden_dim, output_dim)

# 初始化参数梯度
grad_U = np.zeros_like(U)
grad_V= np.zeros_like(V)
grad_W = np.zeros_like(W)

iterations = 20000
# 训练过程：不使用batch
for i in range(iterations):
    # 生成一个简单的加法问题 （a+b = c), a, b 除以2防止c溢出
    a_int = np.random.randint(largest_number / 2)
    a = int2binary[a_int]
    b_int = np.random.randint(largest_number / 2)
    b = int2binary[b_int]

    c_int = a_int + b_int
    c = int2binary[c_int]

    d = np.zeros_like(c)
    # 训练样本
    X = np.array([a, b]).T
    y = np.array([c]).T

    loss = 0  # 损失函数

    hs = []  # 保存每个时间步长下的隐含特征
    hs.append(np.zeros((1, hidden_dim)))  # 初始化0时刻特征为0
    os = []  # 保存每个时间步长的预测值

    # forward过程
    for t in range(binary_dim):
        # 当前时刻特征
        xt = X[binary_dim - t - 1]
        # 隐含层
        ht = sigmoid(xt.dot(U) + hs[-1].dot(W))
        # 输出层
        ot = sigmoid(ht.dot(V))
        # 存储结果
        hs.append(ht)
        os.append(ot)
        # 计算loss，采用L1
        loss += np.abs(ot - y[binary_dim - t - 1])[0][0]
        # 预测值
        d[binary_dim - t - 1] = np.round(ot)[0][0]

    # backward过程
    future_d_ht = np.zeros((1, hidden_dim))  # 从上一个时刻传递的梯度
    for t in reversed(range(binary_dim)):
        xt = X[binary_dim - t - 1].reshape(1, -1)
        ht = hs[t+1]
        ht_prev = hs[t]
        ot = os[t]
        # d_loss/d_ot
        d_ot = ot - y[binary_dim - t - 1]
        d_ot_output = sigmoid_derivative(ot) * d_ot
        grad_V += ht.T.dot(d_ot_output)
        d_ht = d_ot_output.dot(V.T) + future_d_ht  # 别忘来了上一时刻传入的梯度
        d_ht_output = sigmoid_derivative(ht) * d_ht
        grad_U += xt.T.dot(d_ht_output)
        grad_W += ht_prev.T.dot(d_ht_output)

        # 更新future_d_ht
        future_d_ht = d_ht_output.dot(W.T)

    # SGD更新参数
    U = U - learing_rate * grad_U
    V = V - learing_rate * grad_V
    W = W - learing_rate * grad_W
#----------------------------------
    # 重置梯度
    grad_U *= 0
    grad_V *= 0
    grad_W *= 0
#----------------------------------
    # 输出loss和预测结果
    if (i % 1000 == 0):
        print("loss:" + str(loss))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")

结果：

loss:5.00127631787096
Pred:[1 1 1 1 1 1 1 1]
True:[0 0 1 1 0 0 0 1]
25 + 24 = 255
------------
loss:4.078095061903546
Pred:[0 0 0 0 0 0 1 0]
True:[0 1 1 0 1 0 0 1]
1 + 104 = 2
------------
loss:3.9446123086840794
Pred:[0 1 0 0 0 1 1 1]
True:[1 0 0 1 0 1 1 1]
117 + 34 = 71
------------
loss:3.3648771518000866
Pred:[0 0 0 0 0 0 1 0]
True:[0 1 1 1 0 0 1 0]
74 + 40 = 2
------------
loss:2.8204597278431844
Pred:[1 0 0 1 1 0 1 1]
True:[1 0 0 1 0 0 1 1]
100 + 47 = 155
------------
loss:1.121107524667487
Pred:[0 0 0 1 1 0 0 1]
True:[0 0 0 1 1 0 0 1]
17 + 8 = 25
------------
loss:0.9348100261952509
Pred:[0 1 1 1 1 0 1 0]
True:[0 1 1 1 1 0 1 0]
28 + 94 = 122
------------
loss:0.5565792149240794
Pred:[0 1 1 0 0 1 1 0]
True:[0 1 1 0 0 1 1 0]
81 + 21 = 102
------------
loss:0.42942078786941507
Pred:[0 0 1 0 0 1 0 0]
True:[0 0 1 0 0 1 0 0]
30 + 6 = 36
------------
loss:0.4385399024946841
Pred:[1 1 0 0 0 1 1 1]
True:[1 1 0 0 0 1 1 1]
74 + 125 = 199
------------
loss:0.28472002755796516
Pred:[1 0 1 0 1 1 1 1]
True:[1 0 1 0 1 1 1 1]
106 + 69 = 175
------------
loss:0.3385665267460839
Pred:[1 0 0 1 1 0 0 1]
True:[1 0 0 1 1 0 0 1]
83 + 70 = 153
------------
loss:0.289729466127258
Pred:[0 1 1 0 0 0 0 1]
True:[0 1 1 0 0 0 0 1]
74 + 23 = 97
------------
loss:0.3140939999708829
Pred:[0 1 1 1 0 0 0 0]
True:[0 1 1 1 0 0 0 0]
57 + 55 = 112
------------
loss:0.24482058057440437
Pred:[0 1 0 1 0 0 0 0]
True:[0 1 0 1 0 0 0 0]
69 + 11 = 80
------------
loss:0.2918368794687556
Pred:[1 0 0 1 0 0 1 0]
True:[1 0 0 1 0 0 1 0]
110 + 36 = 146
------------
loss:0.26259882762101444
Pred:[1 1 0 0 1 0 1 0]
True:[1 1 0 0 1 0 1 0]
96 + 106 = 202
------------
loss:0.24672624391748108
Pred:[1 0 0 0 1 0 0 1]
True:[1 0 0 0 1 0 0 1]
115 + 22 = 137
------------
loss:0.18003675347822368
Pred:[1 1 0 0 0 1 1 0]
True:[1 1 0 0 0 1 1 0]
115 + 83 = 198
------------
loss:0.22102609505269238
Pred:[1 0 1 0 1 1 1 0]
True:[1 0 1 0 1 1 1 0]
82 + 92 = 174
------------

最后

以上就是年轻诺言为你收集整理的RNN代码实现的全部内容，希望文章能够帮你解决RNN代码实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。