统计学(三)：置信区间; Z 检验(样本平均数的假设检验), 均值分布, 附Python实现（大牌护肤品碧欧泉背后的秘密）均值分布均值分布的假设检验：Z检验置信区间模拟问答后记

引言

  本篇博文开始前，请熟知如下链接中的概念；当然，如果直接开始，遇到遗忘的统计学名词再返回查找也没问题。

统计学(二)：假设检验导论 (深入浅出超详解，附Python 代码)；置信区间与 Z 检验先修

  统计学(二)中关于金钱与幸福指数的案例，它的样本只有一个被试。然而，正如我们所说的那样，在实际的例子当中，各领域的研究中大多数都是一个样本中包含着许多个体。所以本篇博文将考虑样本不止一个个体的假设检验。

  大牌护肤品碧欧泉的广告已经渗透到笔者的浏览器首页了，错点开一看，发现与商品效果有关的数字很诱人。

  正好笔者母亲准备生日，既然那么多女性给出的反馈都是好好好，就想着要不要搞一下？正犹豫之时，突然看到下面这行小字

  也就只给了62名女性试用，就好意思得出这样牛逼的结论？但鉴于碧欧泉以前的口碑，所以这62名女性说是随机抽样来的这点可以相信(如果不是随机抽样，即都请些偏袒碧欧泉的人来检测，那就太说不过去了)。为了更好的探究这个得到了试用装样本的群体的评分情况是否真的能够反映出产品效果优良与否，笔者对他们的评分数据进行了假设检验(Z检验)，并得出了结论。

  下面这幅图是一般女性（不使用该款碧欧泉产品）对自己肌肤清新度的评分情况，已知平均值和标准差。清新度、细致度和干净度这三个维度都是需要探究的，因为假设检验的步骤相同，只是利用的数据不同而已，所以笔者这里以清新度为例。

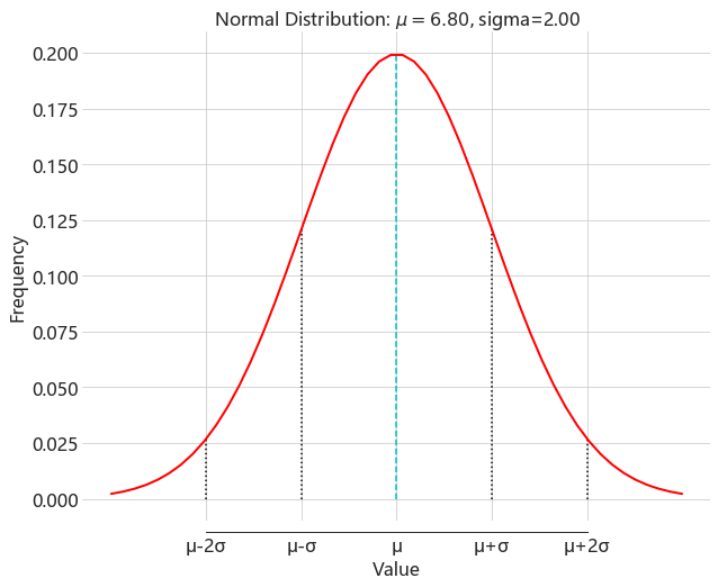
  评分还可以，平均分为6.8，标准差为2。现在，碧欧泉所在的研究团队随即招募了含62个个体的样本来试用碧欧泉的新产品，使用周期为大约28天。调研结束后，包含着62个个体的评分结果也随之出炉。在这个包含多个个体的小样本中，我们也拿到了一个 平均值：7.3 那我们该如何评估刚才提出的“碧欧泉家的这款新产品(小绿蛋)对肌肤清新度的影响”呢？

问：既然平均值已经高于6.8了，为什么不可以直接下定论呢？

答：7.3这个评分只是62个人的评分的平均值，你哪里来的自信，而6.8这个平均分是针对总体而言的，即数据来源是数以万计的女性评分。

问：为了是结论具有更大的说服力，我们为何不增大样本中的个体数量呢？根据大数定律可知当样本数量越来越大时，统计量(样本的数值概要)也会更接近参数(总体的数值概要)？

答：统计学(二)已经讲得很清楚了，资源有限，动不动就给几千甚至几万女性试用新产品，也太奢侈了吧…

均值分布

均值分布的官方概念

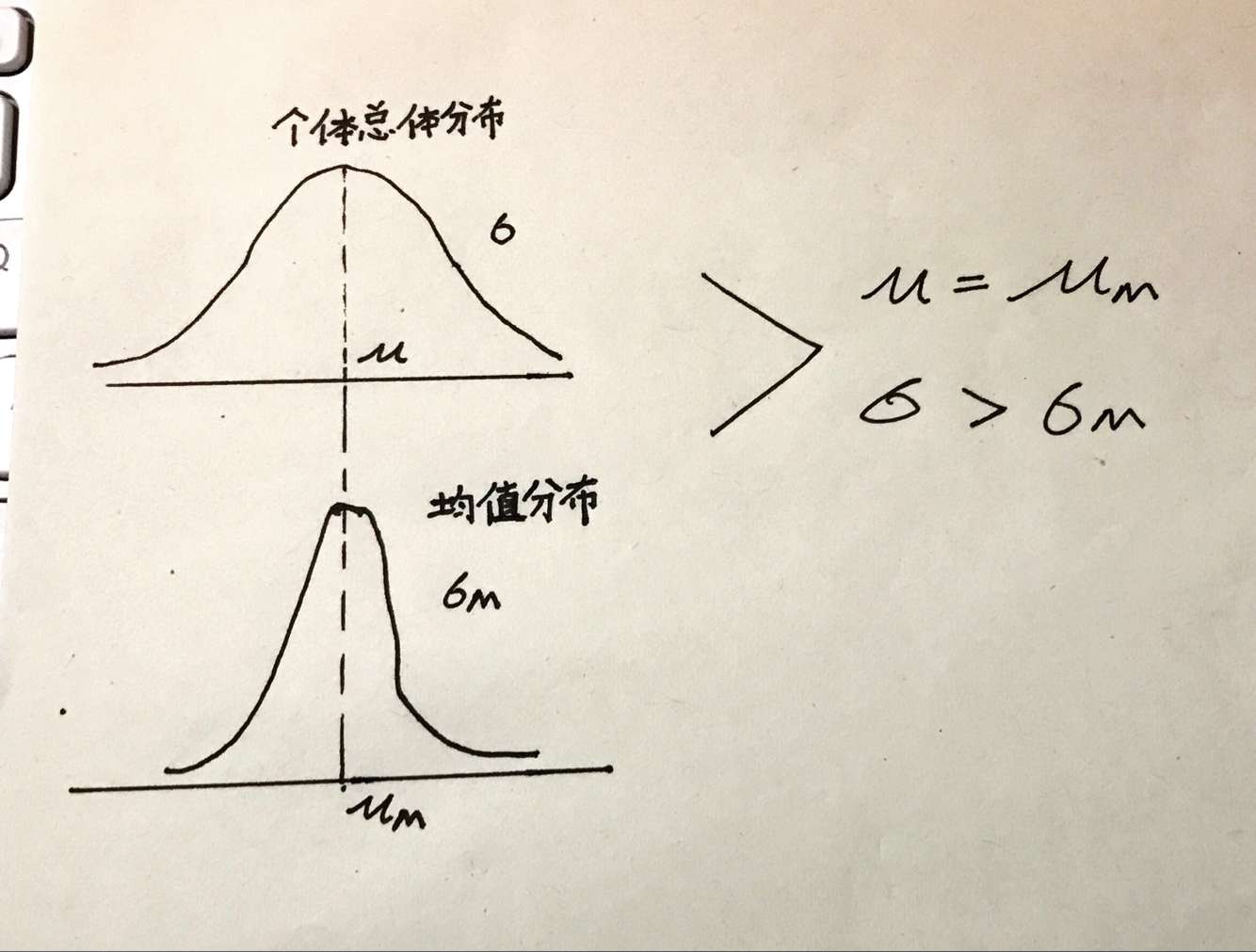
均值分布  总体中给出一定规模的样本的平均数的分布（也称为平均数的抽样分布）；当假设检验涉及的样本中不止一个个体时，比较分布即均值分布。

为什么需要均值分布

再次强调，请确保你已经完全理解了 Z分数 的含义

  教材概念：均值分布是许多具有相同规模的样本的平均数的分布，每个样本都是随机地从具有相同个体的总体中抽取出来的。(统计学家也称这种平均数的分布为平均数的抽样分布。而均值分布这个词可以使我们更好的明白讨论的是平均数的总体，而不是样本或者某种样本分布)

  统计学(一)+(二)中，我们已经知道将某一个个体的原始分数转化为Z分数后，可通过查表或粗略估计两种方法得到TA的段位情况；其中比较分布中的数据是由一个个个体分数组成的。所以对单个个体求z分数，并将其与由一个个单个个体组成的分布进行比较，合情合理。但现在我们希望知道这个样本(包含了多个独立个体)的平均数情况，如果比较分布还是由个体组成的话，那就有点“错配”的感觉了，这个时候我们就需要祭出均值分布了。

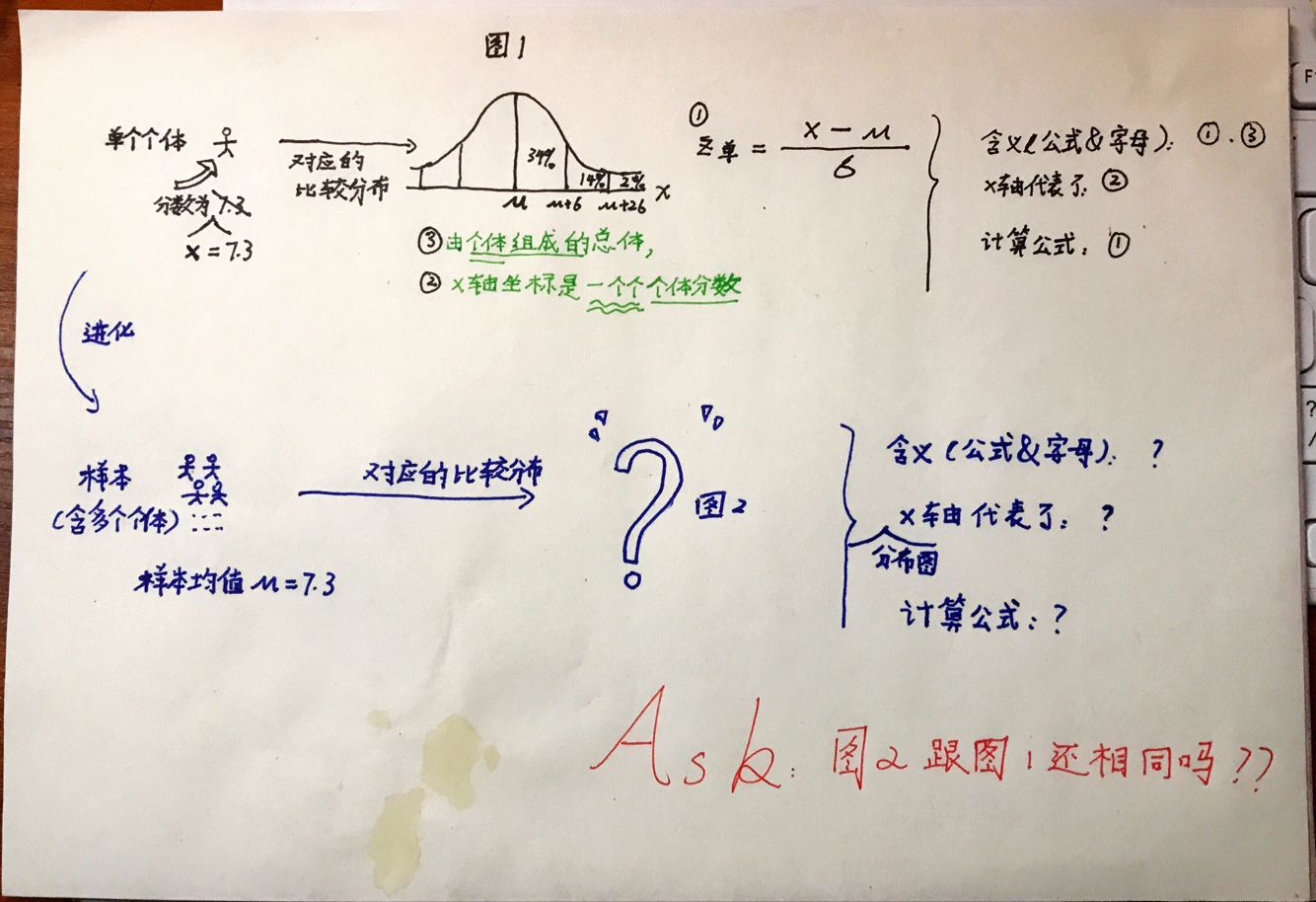
均值分布的通俗理解？

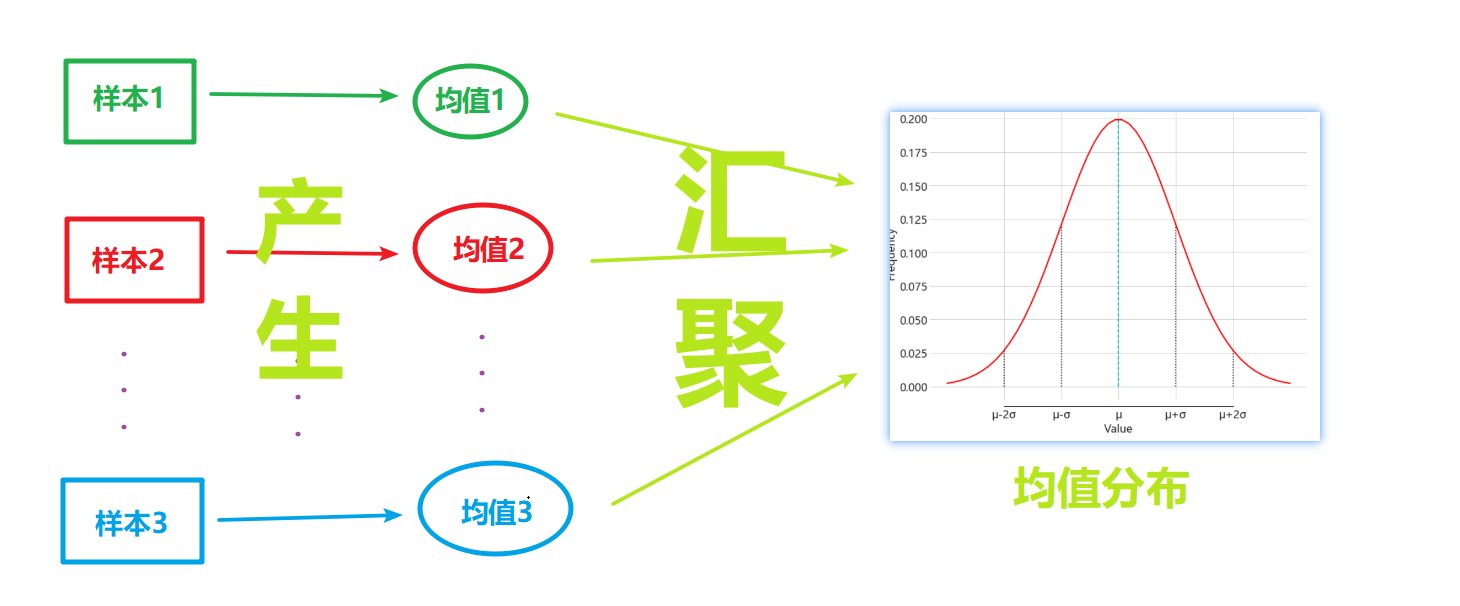
  如果觉得均值分布这个词有点微绕的话，那就一句话：什么是分布？无三不成几，只有多个单一个体组成一个小群体，才有“分布”一词之说。均值分布，均值的分布，即这个分布中有许多均值。均值怎么来？均值从一个包含多个个体的样本中来。所以要想得到均值的分布，我们需要下一番苦功。生成过程如下

均值分布的特征

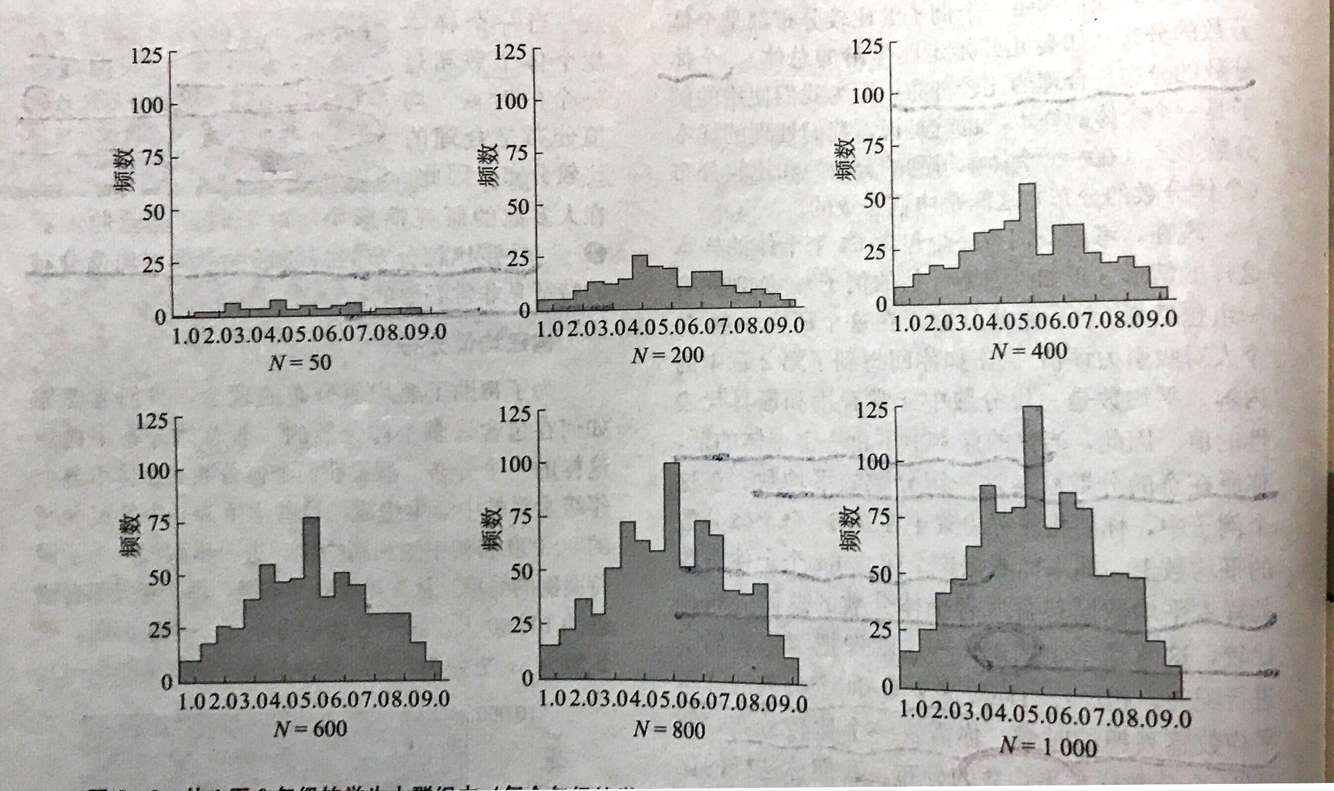
  从通俗理解中我们可知，要想得到一个包含多个个体的样本的均值分布（这个样本的比较分布，用来确定这个样本的平均值处在什么段位，是比一般总体显著要高还是要低），需要下一番苦功。根据均值分布通俗理解的图，研究小组每次从这个样本（含62个个体）中随机抽出2个个体并求其平均分，N 抽取的次数，可以看出，随着 N 的增大，均值分布的形态也越来越接近正态分布，而且分布情况也开始美观起来（不再是那么低矮）

  然而幸运的是，我们可以利用一些简单的法则直接得出均值分布的特征，甚至可以不用一个样本。我们仅仅需要的信息是

• 包含个体的总体分布特征
• 每个样本中的分数的数量

为了更好的理解均值分布的特征，笔者直接进行揭密，后再逐一拆解。

均值分布的平均值和标准差

法则1：均值分布的平均数与包含众多个体的总体的平均数是一样的

$${\mu }_M=\mu$$

  ${\mu }_m$是均值分布的平均数，$\mu$时包含众多个体的总体的平均数。

问：明明调研样本只有62个，总体有成千上万个，均值分布的平均数和包含众多个体的总体的平均数还会一样？

答：每一个样本（不止一个个体）都是以从包含众多个体的总体中随机选择出来的个体为基础的。因此，样本的平均数比起包含众多个体的总体平均数来说时高时低。然而，在构建均值分布时，因为选择过程是随机的且我们选取了很多样本。最后，较高的平均数和较低的平均数就完美抵消了。

法则2：这条法则是关于离散程度的。均值分布的方差比总体的方差要小，计算公式如下

$${\sigma }_M^2=\frac{{\sigma }^2}{N}$$

  其中，${\sigma }_M^2$ 表示均值分布的方差，${\sigma }^2$ 和 $N$ 分别表示总体的方差和每个样本中的个体数量。如果你用的是包含两个分数的样本，不大可能两个分数都是极端的。此外，对于有一个极端平均数的特殊随机样本来说，这两个极端分数在同一方向上(都非常高或都非常低)都会变得非常极端。因此，每个样本中不止一个分数会对这样的样本平均数有一个适度的影响。在任何一个样本呢中，极端值都会由于一个中间分数或是对立方向上的一个极端值而倾向于保持平衡。这使得每个样本平均数趋向于中间趋势而离极端值越来越远。由于极端值越来越少，平均数的方差比由众多个体组成的方差小。所以均值分布的标准差 ${\sigma }_M$ 也就呼之欲出。

$${\sigma }_M=\sqrt{\frac{{\sigma }^2}{N}}$$

法则3：在以下条件下均值分布的形态近似正态分布：a）每个样本包含30个或更多个体。b）总体分布是正态分布

  首先我们需要知道，无论总体分布是什么形态，均值分布都趋向于单峰的和对称的。均值分布趋于单峰态是因为极端值对于保持平衡有着与我们在讨论方差时注意到的相似规律；中间位置的平均数更有可能，极端平均数不大可能；趋于对称是因为非对称(偏态)是由极端值导致的。极端值更少了，非对称也就更少了。

  每个样本中的个体越多，均值分布就越接近正态曲线。尽管均值分布鲜有一个确切的正态曲线，但是包含30个或更多个体的样本（甚至是一个非正态总体），均值分布就会更接近于正态曲线，并且正态曲线表里的百分比也十分精确。（也就是说，样本量大于30具有更胜一筹的近似值，但是对于大多数实践研究来说，样本量为30就足够了。）最后，无论什么时候，只要包含众多个体的总体分布是正态的，不管每个样本中的个体数量是多少，均值分布都是正态的。

休息一下跳个舞再继续吧…

均值分布的假设检验：Z检验

再次强调，请确保你已经完全理解了 Z分数 的含义

  刚才的一顿基础输入完毕后，我们就要开始快马加鞭的进行碧欧泉新产品的调研了。假设检验的几个步骤在统计学(二)假设检验导论中已经非常明确了，简单温习一下。（务必十分清晰步骤）

假设检验的步骤

1. 重申有关总体的研究假设和零假设问题
2. 决定比较分布的特征
3. 根据比较分布上的样本临界值来决定是否应该拒绝零假设
4. 决定比较分布上你的样本分数
5. 决定是否拒绝零假设

  一些比较有经验的老司机会直接将第一步和第三部结合，即明确了研究的问题后就先确定一个标准，再将后续计算出来的结果和这个标准相比对，从而决定是否放宽/加严一点。但第一步往往是被忽视的，毕竟普通的统计学教材和一些考试题都是直接丢给你几句话让你判断，如下图

PS：看到问号后面的小括号中的提示我们还能猜到要用Z检验，但现实情况/业务纷繁复杂，我们怎么知道该选取什么样的检验方式呢？(后续博文)

  如果我们能够探寻其背后的业务背景，即它希望解决的是什么问题/验证的是什么假设？使用的单侧还是双侧检验，该选择什么样的检验方式都通过现实生活来理解的话，就不用在临考前狂刷题和狂背公式了，说来真的惭愧。让我们回到碧欧泉的例子，正式开始进行Z检验！

Z检验实战

步骤1 + 步骤3

确定总体

总体1：一般女性对自己肌肤清新度的评分
总体2：使用了碧欧泉小绿蛋后的女性对自己肌肤清新度的评分

确定研究假设与零假设

研究假设：碧欧泉小绿蛋对女性给出的肌肤清新度评分有影响
零假设：碧欧泉小绿蛋对女性给出的肌肤清新度评分有影响

确定是选择单侧还是双侧Z检验，并确定Z临界值

因为研究假设是探究是否有影响，即怎样影响，所以没有明确的指明方向，视结果而定，所以这里选择双侧检验，取显著性水平 $\alpha =5$，即比较分布中两端各2.5%，Z临界值为正负1.96。即如果计算出来的Z值大于1.96或小于-1.96，我们就要拒绝零假设。

步骤2 + 步骤4

决定比较分布的特征

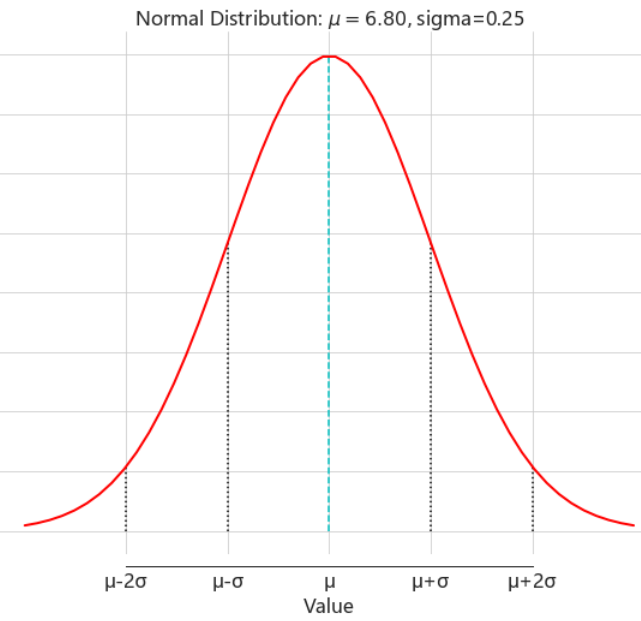
  根据碧欧泉调研小组手头上的数据可知，一般总体(没有使用产品)分布中，$\mu =6.8$，$\sigma =2$，样本平均数 $M=7.3$ 再根据上面提高的均值分布对应的平均数和标准差的计算公式，可得 ${\mu }_M=\mu =6.8$，${\sigma }_M=\sqrt{\frac{{\sigma }^2}{N}}=\sqrt{\frac{2^2}{62}}=0.25$，又因为这个样本超过了30个个体(62位女性受试)，均值分布的形态就是近似正态分布，如下图(注意看标标准差)

计算比较分布上你的样本分数

  统计学(二)假设检验导论中已经清晰的说到，比较分布即是零假设成立时的分布，我们现在计算比较分布上的样本分数，旨在查看其是否超过了我们期望的临界值，在Z检验中，临界值又可被称为Z临界值。

$$Z=\frac{M-{\mu }_M}{{\sigma }_M}=\frac{7.3-6.8}{0.25}=2$$

步骤5：决定是否拒绝零假设

  我们设置的拒绝零假设的最小正Z分数是+1.96。样本平均数的Z分数为+2，因此，碧欧泉调查小组能够拒绝零假设且得出研究假设是被支持的，换句话说，Z检验的结果在p<0.05水平上具有统计显著性。拒绝过程如图

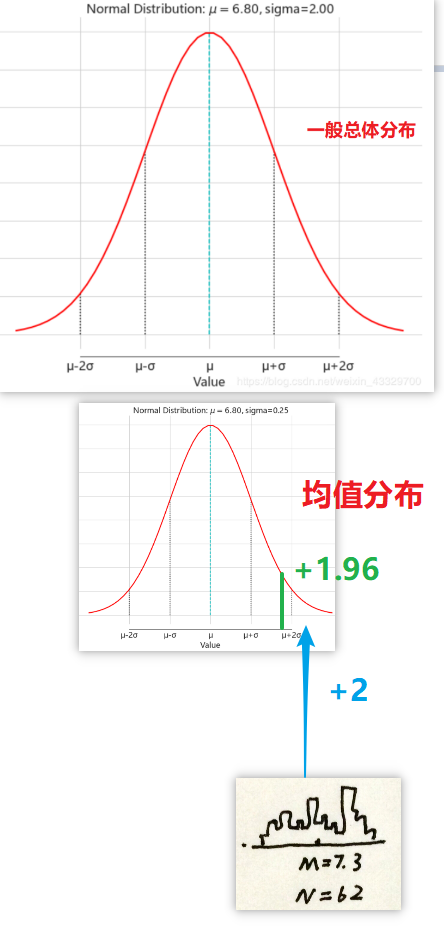
看来碧欧泉的这款产品对提升肌肤清新度还是有用的。

置信区间

为什么需要置信区间

  当总体平均数未知，对总体平均数最好的估计值就是样本平均数。但是，用样本平均数作为总体平均数的估计值究竟有多精确呢？解决这个问题就必须解决 “从总体中抽取的样本的平均数如何变化” 这一问题。幸运的是当考虑均值分布时，我们就已经思考了这个问题。

从总体中得出的样本平均数的变异就是均值分布的变异。均值分布的标准差、平均数的标准误，都是对样本平均数与总体平均数相比变异多少的测量。

什么是置信区间(CI: Confidence Interval)

大致来说很可能包括真正总体平均数的分数范围（即较高和较低值之间的分数）；更加准确地说，即从中能得到你的样本平均数的概率很高的可能均值范围

又绕了？来看看下面的图吧，统计学(一)中的Z分数分布图已经非常清晰了

  以中国女性平均身高(平均158cm-百度百科)为例，其分布是如上图的正态分布，知道均值(158)和标准差(x)。那我们可以大胆的说出如下话语：

• 中国女性的身高100%分布在这个分布图中(这是肯定的，已经包含了异常值)
• 百分之68%（我们有68%的自信）的中国女性的身高在158加减x之间
• 百分之96%（我们有96%的自信）的中国女性的身高在158加减2x之间
• 以此类推…

95%的置信区间  该置信区间就是有95%的概率总体平均数会落入这个区间之内

置信区间怎么求

  既然是一个区间，那就有上下界限，这两个界限统称为置信界限。对于单个样本来说，我们想知道自己有百分之多少信心能确定它落在哪个范围，只需要对照个体总体的分布图，上面最近的那副，知道这个个体总体的标准差，然后照着套就行，$X-\sigma =158-x,X+\sigma =158+x$，所以我们有68%的自信认为中国女性的平均身高落在 [158-x, 158+x] 这个区间中。顺便说一下，你越自信，给自己留的后路就越要多些。笔者有百分之一百二十的自信确定自己的年收入在1~100万间（虽然很荒谬）。所以置信度/置信水平/自信程度越大，置信区间就越宽。

  换算成均值分布的置信区间，只需要将字母改一下而已，原理还是一样的。

$$X\pm \sigma \Rightarrow M\pm {\sigma }_M\Rightarrow X\pm \frac{\sigma }{N}$$

不说了我先去买礼物了，Python 实现见底部链接

模拟问答

• 具有超过一个个体的样本的假设检验与只有一个个体的样本的假设检验有什么不同。
• 什么是均值分布
• Z 检验是什么，有什么用，公式？
• 95%的置信区间又是什么意思，如何计算？
• 置信度与置信区间的关系
• 什么时候选择单样本Z检验，双样本Z检验，单样本t检验，双样本t检验，卡方检验等等(后续博文)

后记

延伸阅读

• 统计学(二)：假设检验导论 (深入浅出超详解，附Python 代码)；置信区间与 Z 检验先修

精彩回顾

• Python 绘制正态曲线：linespace 组合 matplotlib(放入自写库，一行代码实现复杂绘图)
• Excel 浏览大表格的坑 – 这几个快捷键与技巧，轻松避坑，效率加倍(金融实战)

  数据分析，商业实践，数据可视化，网络爬虫，统计学，Excel，Word, 社会心理学，认知心理学，行为科学，民族意志学 各种专栏后续疯狂补充

  欢迎评论与私信交流！

最后

以上就是贪玩火龙果为你收集整理的统计学(三)：置信区间; Z 检验(样本平均数的假设检验), 均值分布, 附Python实现（大牌护肤品碧欧泉背后的秘密）均值分布均值分布的假设检验：Z检验置信区间模拟问答后记的全部内容，希望文章能够帮你解决统计学(三)：置信区间; Z 检验(样本平均数的假设检验), 均值分布, 附Python实现（大牌护肤品碧欧泉背后的秘密）均值分布均值分布的假设检验：Z检验置信区间模拟问答后记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。