递归—汉诺塔、青蛙跳台阶问题、斐波那契数前言一、递归二、案列总结

前言

基于Java实现的递归的经典案例。

一、递归

相当于数学中的归纳法
两个条件：
（1）有一个起始条件——“归”。
（2）有一个递推公式——“递”。

二、案列

1.斐波那契数

斐波那契数列：
1、1、2、3、5、8、13、21、34…
递推公式：
F(1)=1，F(2)=1,
F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

代码如下（示例）：

 public static int fib(int n) {
        if(n == 1 || n == 2){
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }

递归的效率比较低，面试的时候最好用非递归的

（2）非递归

使用循环的方法，效率会有很大的提升。

代码如下（示例）：

public static int fib2(int n) {
        if(n == 1 || n == 2){
            return 1;
        }
        int f1 = 1;
        int f2 = 1;
        int f3 = 0;
        for (int i = 3; i <= n; i++) {
            f3 = f1 + f2;
            f1 = f2;
            f2 = f3;
        }
        return f2;
    }

2.青蛙跳台阶

一只青蛙跳台阶每次只能跳一个或二个台阶，有n阶台阶的时候有多少种跳法？
1台阶：1种；
2台阶：2种;->（1,1）/（2）
3台阶：3种;->（1,1,1）/ (1,2) / (2,1）
4台阶阶：5种;->(1,1,1,1)/ (1,1,2) / (1,2,1) / (2,1,1) / (2,2)
…
n台阶：f(n-1)+f(n-2) , n>2

这个和斐波那契数列得出的规律差不多。

代码如下（示例）：

public static int jumpStage(int n) {
        if(n == 1 || n == 2) {
            return n;
        }
        return jumpStage(n - 1) + jumpStage(n -2);
    }

3.汉诺塔

这个可能理解起来有点麻烦，但是用递归实现却很简单。
假设有三个塔
A:起始位置，放了n个盘子
B:中转位置
C:目标位置（就是需要将A上的盘子移动到C上）
代码思路图大致如下：

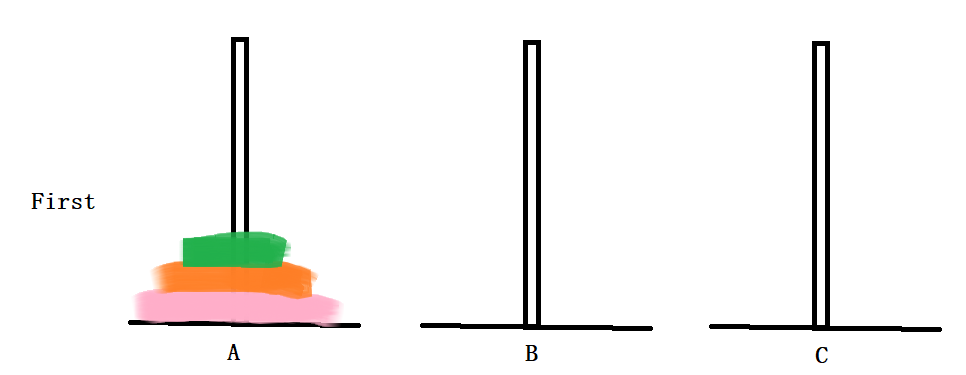
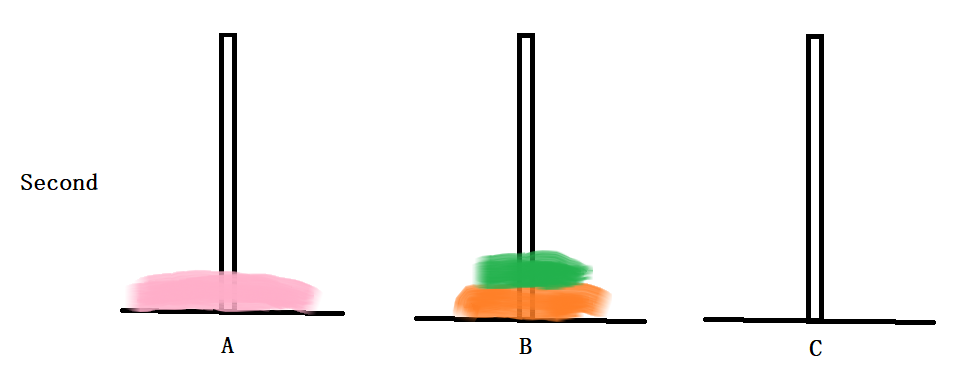
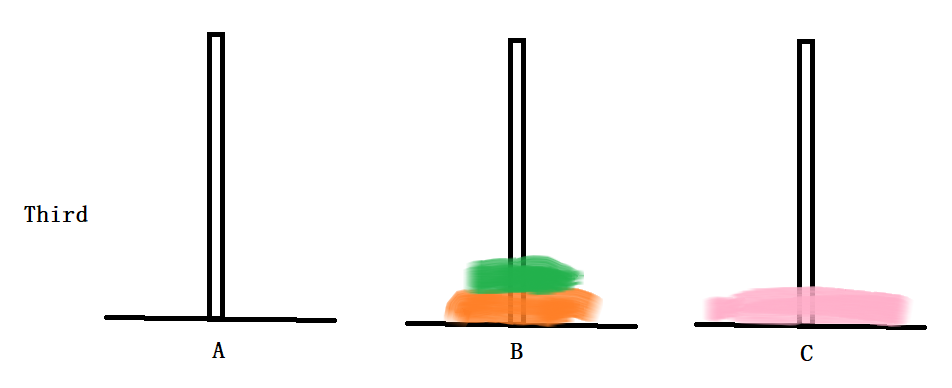
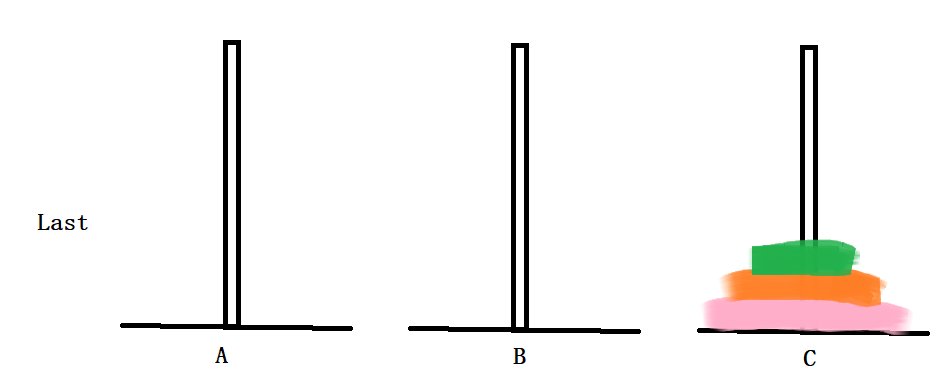
代码如下（示例）：

/**
     * 相当于与一个能移动东西的工具
     * @param start 起始位子
     * @param end 目标位子
     */
    public static void move(char start,char end){
        System.out.print(start+"->"+end+" ");
    }

    /**
     * 汉诺塔
     * @param n 盘子的个数
     * @param start 盘子的位置
     * @param mid 中转位置
     * @param end 目标位置
     */
    public static void hanio(int n,char start,char mid,char end){
        if(n == 1){
            move(start,end);//只有一个直接从A->C
        }else {
            hanio(n-1,start,end,mid);//把n-1个盘子移到中转位子上
            move(start,end);//将剩下的一个移到目标位子上
            hanio(n-1,mid,start,end);//再将n-1个盘子移到目标位子上
        }
    }

总结

递归主要是要有‘递’和‘归’，摸清套路就很好上手。上文使用的方法递归，方法就是C语言中的函数。

最后

以上就是优秀雪糕为你收集整理的递归—汉诺塔、青蛙跳台阶问题、斐波那契数前言一、递归二、案列总结的全部内容，希望文章能够帮你解决递归—汉诺塔、青蛙跳台阶问题、斐波那契数前言一、递归二、案列总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。