C语言青蛙跳台阶【图文详解】前言

前言

在本文，我们要与一只活泼可爱的小青蛙合作，带领着它跳上台阶，这个小家伙精力充沛，特别擅长于跳跃。我们要让它做我们的思维助手，看看有多少种方法让它跳到指定的台阶上。

本文比较生动有趣，没有太多的理论，小青蛙也非常敬业，相信对你来说，阅读本文将是一个愉快的经历，如果有什么建议，可以评论留言我，恒川都会认真看的哦。

我还得温馨地提醒一下你：

本文易懂（不难），但还是值得琢磨的。有些思维方法乍一眼看起来很像，代码写出来似乎也差不多，但是它们之间的解题方法，确实有差别的，你可能需要仔细体会，才能领悟。
如果想看汉诺塔的讲解，请点击该链接汉诺塔详细图解。

1. 题目介绍

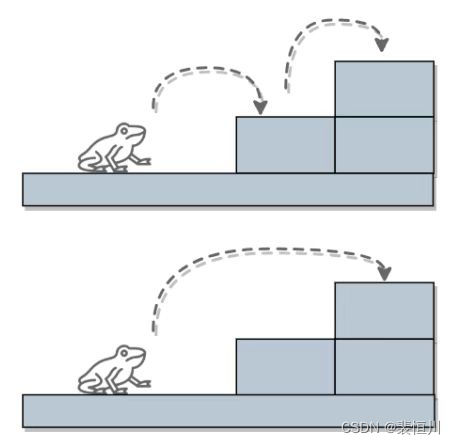
一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,例如:跳上第一级台阶只有一种跳法:直接跳 1 级即可。跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级.
问要跳上第 n 级台阶有多少种跳法?

2. 解题思路

此类求多少种可能性 的题目一般都有递推性质 ，跟斐波那契，汉诺塔的题型相似，即 f(n)和 f(n-1)…f(1)之间是有联系的。
如果想看汉诺塔的讲解，请点击该链接汉诺塔详细图解

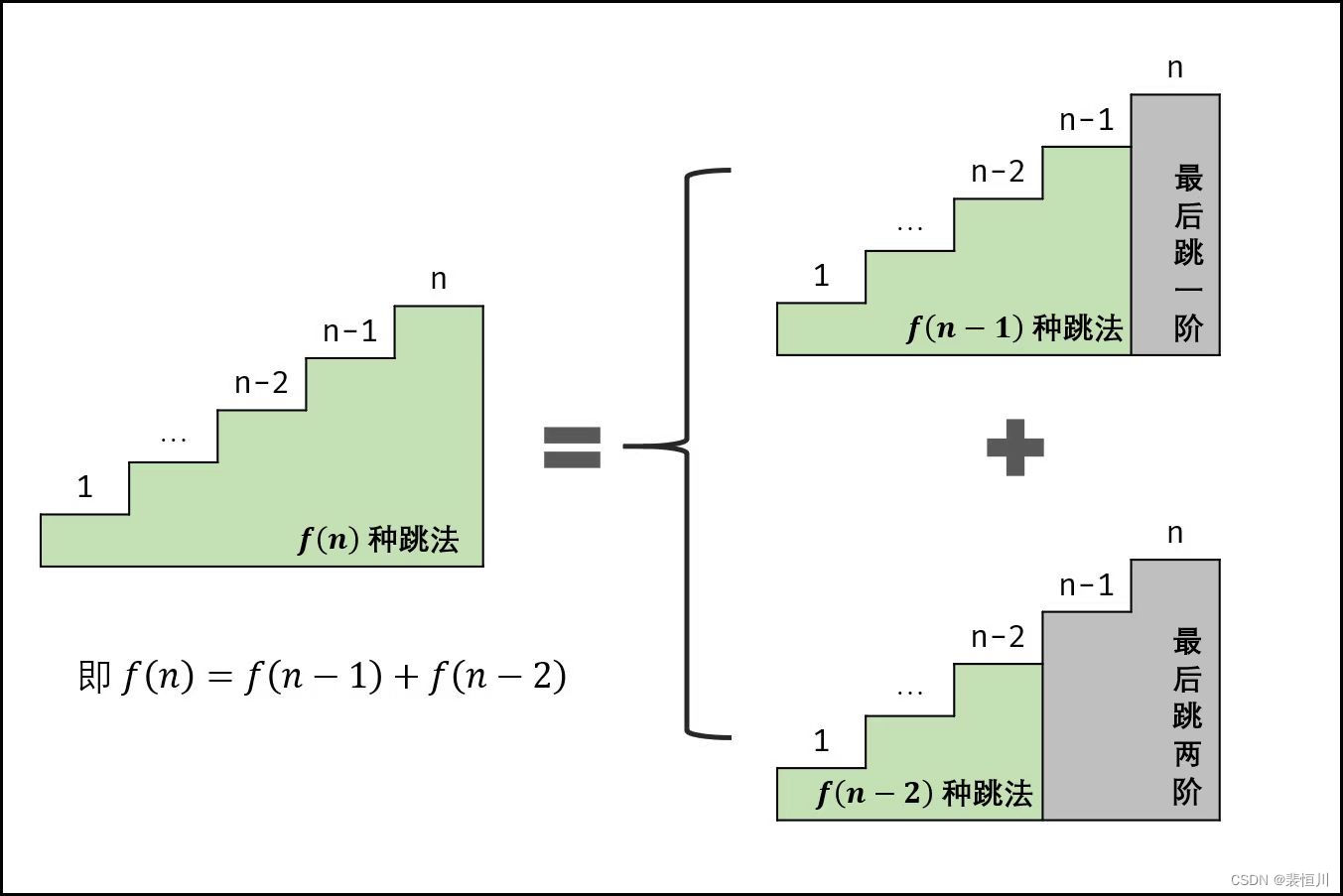
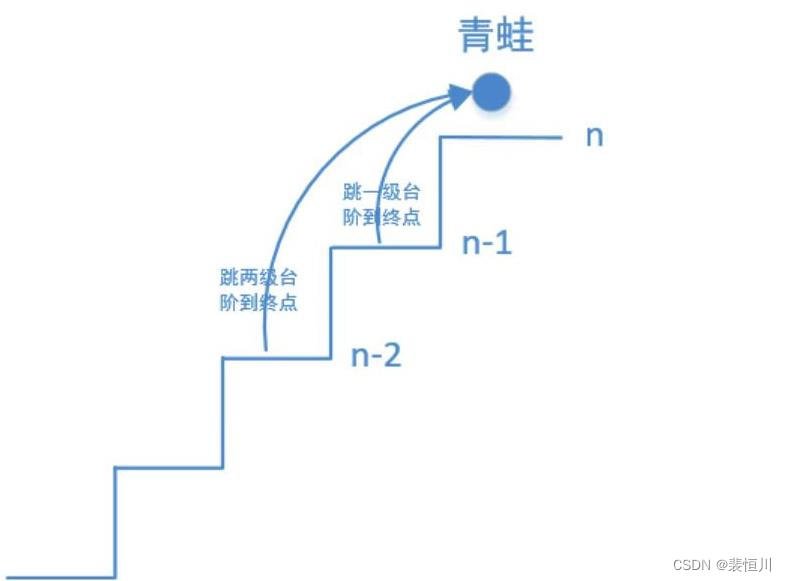
设跳上 n级台阶有 f(n)种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上1级或 2级台阶。
当为 1级台阶： 剩 n-1个台阶，此情况共有 f(n-1)种跳法；
当为 2级台阶： 剩 n-2个台阶，此情况共有 f(n-2)种跳法。
f(n)为以上两种情况之和，即 f(n)=f(n-1)+f(n-2)，以上递推性质为斐波那契数列。本题可转化为求斐波那契数列第 n项的值 ，与斐波那契数列等价，唯一的不同在于起始数字不同。
青蛙跳台阶问题： f(0)=1 , f(1)=1, f(2)=2；
斐波那契数列问题： f(0)=0 , f(1)=1, f(2)=1。

斐波那契数列的定义是 f(n + 1) = f(n) + f(n - 1)，生成第n项的做法有以下几种：

递归法：
原理： 把 f(n)问题的计算拆分成 f(n-1)和 f(n-2)两个子问题的计算，并递归，以 f(0)和 f(1)为终止条件。
缺点： 大量重复的递归计算，例如 f(n)和 f(n - 1)两者向下递归都需要计算 f(n - 2)的值。

记忆化递归法：
原理： 在递归法的基础上，新建一个长度为 n的数组，用于在递归时存储 f(0)至 f(n)的数字值，重复遇到某数字时则直接从数组取用，避免了重复的递归计算。
缺点： 记忆化存储的数组需要使用 O(N)的额外空间。

动态规划：
原理： 以斐波那契数列性质 f(n + 1) = f(n) + f(n - 1)为转移方程。
从计算效率、空间复杂度上看，动态规划是本题的最佳解法。

链接：https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/solution/mian-shi-ti-10-ii-qing-wa-tiao-tai-jie-wen-ti-dong/
来源：力扣（LeetCode）

3. 利用图片来演示青蛙跳台阶的原理

4. 如何用C语言实现青蛙跳台阶

#include<stdio.h>
int dance_s(int n)
{
	if (n == 1)
	{
		return 1;//当只有一层台阶时直接返回1
	}
	if (n == 2)
	{
		return 2;//当只有2层台阶时直接返回2
	}
	if (n > 2)
	{
		return dance_s(n - 1) + dance_s(n - 2);
	}//当n>2时，利用递归，直到结束停止
}
int main()
{
	int n = 0;
	scanf("%d", &n);//输入台阶的个数
	int num = dance_s(n);
	printf("%dn", num);//打印共有多少种跳台阶的方案
	return 0;
}

如果这份博客对大家有帮助，希望各位给恒川一个免费的点赞作为鼓励，并评论收藏一下，谢谢大家！！！
制作不易，如果大家有什么疑问或给恒川的意见，欢迎评论区留言。

最后

以上就是高高人生为你收集整理的C语言青蛙跳台阶【图文详解】前言的全部内容，希望文章能够帮你解决C语言青蛙跳台阶【图文详解】前言所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。