ac数论之逆元取模--快速冥取大数模--二分乘--二分加--素数打表--因子提取及其记数--Sumdiv

Description

Input

Output

Sample Input

2 3

Sample Output

15

Hint

Source

Romania OI 2002

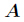
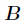
题意：给定两个正整数和，求的所有因子和对9901取余后的值。

 

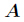
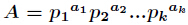
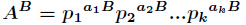
分析：很容易知道，先把分解得到，那么得到，那么

     的所有因子和的表达式如下

所以我们有两种做法。第一种做法是二分求等比数列之和。

#include<iostream>
#include<string.h>
using namespace std;
#define MAXN 10010
#define M 9901
bool prime[MAXN];
int p[MAXN];
void db()//筛选法
{
int cnt=0;
memset(prime,true,sizeof(prime));
for(int i=2;i<MAXN;i++)
{
if(prime[i]==true)
{
p[cnt++]=i;
for(int j=i+i;j<MAXN;j+=i)
{
prime[j]=false;
}
}
}
}
long long power(int a,int n)//快速幂
{
long long result=1;
a=a%M;
while(n>0)
{
if(n%2==1)
{
result*=a;
result%=M;
}
a*=a;
a%=M;
n/=2;
}
return result;
}
long long sum(long long a,long long n)//然而这种递归的形式进行二分加
{
if(n==1)
{
return a;
}
long long
t=sum(a,n/2)%M;//1
if(n%2==1)
{
long long cur=power(a,n/2+1);//2
t=(t+t%M*cur%M)%M;//1+3
t=(t+cur)%M;
}
else
{
long long cur=power(a,n/2);//1
t=(t+t%M*cur%M)%M;
}
return t;
}
long long solve(long long a,long long b)//利用公式求得结果
{
long long result=1;
for(int i=0;p[i]*p[i]<=a;i++)
{
int num=0;
while(a%p[i]==0)
{
a/=p[i];
num++;
}
result*=(sum(p[i],num*b)+1)%M;
result%=M;
}
if(a>1)
{
result*=(1+sum(a,b))%M;
result%=M;
}
return result;
}
int main()
{
long long a,b;
db();
while(cin>>a>>b)
{
if(b==0)
cout<<1<<endl;
else
cout<<solve(a,b)<<endl;
}
}

第二种方法就是用等比数列求和公式，但是要用逆元。用如下公式即可

由于(a/b)%m!=(a%m)/(b%m),如果a太大，那么就麻烦了，所以要求(a/b)%m就要用到逆元

当然比较无脑的一种是用java，可以通过bigDecimal类来解决数太大这个wenti

 

                     

 

因为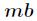可能会很大，超过int范围，所以在快速幂时要二分乘法。

#include<iostream>
#include<string.h>
using namespace std;
#define M 9901
#define MAXN 10010
int p[MAXN];
bool prime[MAXN];
long long multi(long long a,long long
b,long long m)
//二分大数相乘取模
{
long long ans = 0;
a %= m;
while(b)
{
if(b%2== 1)
{
ans = (ans + a) % m;
}
b /= 2;
a = (a + a) % m;
}
return ans;
}
long long fast_power( long long a,long long n,long long m)
{
long long result=1;
a%=m;
while(n>0)
{
if(n%2==1)
{
result=multi(a,result,m);//由于m=M*(p[i]-1)有可能是12位 当a本身是一个很大的质数的时候，long long 放不开
result%=m;
}
a=multi(a,a,m);
a%=m;
n/=2;
}
return result;
}
void db()
{
memset(prime,true,sizeof(prime));
int cnt=0;
for(int i=2; i<MAXN; i++)
{
if(prime[i])
{
p[cnt++]=i;
for(int j=i+i; j<MAXN; j+=i)
{
prime[j]=false;
}
}
}
}
long long solve(long long a,long long b)
{
// long long m=M*()
long long ans=1;
for(int i=0; p[i]*p[i]<=a; i++)
{
if(a%p[i]==0)
{
int num=0;
while(a%p[i]==0)
{
num++;
a/=p[i];
}
long long m=M*(p[i]-1);
ans*=((fast_power(p[i],1+b*num,m)-1)%m);
ans/=(p[i]-1);
ans%=M;
}
}
if(a>1)//当a本身是一个很大的质数的时候
{
long long m=(a-1)*M;
ans*=((fast_power(a,1+b,m)-1)%m);
ans/=(a-1);
ans%=M;
}
return ans;
}
int main()
{
long long a,b;
db();
while(cin>>a>>b)
{
cout<<solve(a,b)<<endl;;
}
}

求逆元的一些方法总结 








求逆元问题是数论中一类比较基础的题目，它常常会与组合数，质数等联系起来。今天我们就来总结一下求逆元的方法，根据数据范围不同有三种，接下来就一一介绍。


-------------------------------------------------------------------------------


方法1.通过扩展欧几里得算法求逆元


这个算法很常见，在这里就不再累述，直接给出代码。
1.求解ax+by=gcd(a,b)，亦即ax≡1(mod b)。函数返回值是a,b的最大公约数，而x即a的逆元。 
2.注意a, b不能写反了。 


3.gcd(a, b) > 1时逆不存在

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void exgcd(ll a,ll b,ll& d,ll& x,ll& y)
{
if(!b) { d = a; x = 1; y = 0; }
else{ exgcd(b, a%b, d, y, x); y -= x*(a/b); }
}
ll inv(ll a, ll p)
{
ll d, x, y;
exgcd(a, p, d, x, y);
return d == 1 ? (x+p)%p : -1;
}
int main()
{
ll a,p;
while(1)
{
scanf("%lld %lld",&a,&p);
printf("%lldn",inv(a,p));
}
}

方法2.通过快速幂求逆元

由于费马小定理，a^(p-1)=1(mod p)-->1/a=a^(p-2)(mod p),故a的逆元为a^p-2.注意这个方法要求模的数必须为质数，传入a和mod-2即可得到结果。

LL quick_inverse(LL n, LL p) {
LL ret = 1,exponent = p;
for (LL i = exponent; i; i >>= 1, n = n * n % mod) {
if (i & 1) {
ret = ret * n % mod;
}
}
return ret;
}

方法3.通过递推求1~n的逆元

我们可以通过inv[i]=inv[p%i]*(p-p/i)%p递推得到逆元。适用于n比较小的情况

int inv[N];
void get_inverse(int n, int p) {
inv[1] = 1;
for (int i = 2; i <= n; ++i) {
inv[i] = (p - p / i) * inv[p % i] % p;
}
}

特殊情况.通过递推求n!

我们可以利用invf[i]=invf[i+1]*(i+1)%p这个公式反递推得到1！~n!的逆元。

int invf[N], factor[N];
void get_factorial_inverse(int n, int p) {
factor[0] = 1;
for (int i = 1; i <= n; ++i) {
factor[i] = i * factor[i - 1] % p;
}
invf[n] = quick_inverse(factor[n], p);
for (int i = n-1; i >= 0; --i) {
invf[i] = invf[i + 1] * (i + 1) % p;
}
}

最后

以上就是激情眼神为你收集整理的ac数论之逆元取模--快速冥取大数模--二分乘--二分加--素数打表--因子提取及其记数--Sumdiv的全部内容，希望文章能够帮你解决ac数论之逆元取模--快速冥取大数模--二分乘--二分加--素数打表--因子提取及其记数--Sumdiv所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。