概述
- 本人的LeetCode账号：魔术师的徒弟，欢迎关注获取每日一题题解，快来一起刷题呀~
- 本人Gitee账号：路由器，欢迎关注获取博客内容源码。
文章目录
- 一、高斯消元法
- 1 模板题
- II 高斯消元法解异或线性方程组
- 二、求组合数
- 1 递推预处理求组合数——N^2
- 2 预处理阶乘求组合数——NLOGN
- 3 卢卡斯(Lucas)定理—询问次数少，数据范围暴大
- 4 精确的计算组合数(非取模意义下)
- 三、卡特兰数
一、高斯消元法
学过线性代数的我们都知道，高斯消元法就是用来求解线性方程组的，对应到代码领域，高斯消元法可以在n^3的时间复杂度内求解n个未知数n个方程的方程组。
解的情况：
- 无解
- 无穷多组解
- 唯一解
这是线性代数中比较基础的一个算法，首先把系数矩阵抽出来，然后对系数矩阵做一些初等行列变换的操作。
就是通过三个基础操作把矩阵变成最简阶梯矩阵。
- 把某一行乘以一个非零的数；
- 交换某两行
- 把某行的若干倍加到另一行上去
这三种操作不会影响方程的解。
把方程化成一个上三角的形式，就能直接求解出来了：
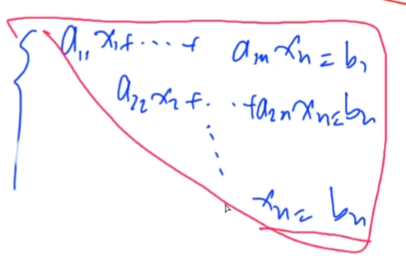
唯一解：如果是一个完美的阶梯型，解就是唯一的。
出现了左边没有未知数，右边的系数是非0的情况，这种情况下就无解。
如果出现很多0 = 0的方程，那么这种情况下就有无穷多解。
1 模板题
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 110;
const double eps = 1e-6;
double a[N][N];
int n;
int gauss()
{
// c表示当前罗列的列 r表示当前最顶上的行是多少
int r, c;
// 罗列每一列
for (c = 0, r = 0; c < n; ++c)
{
// 找到当前每一行的当前列位置绝对值最大的元素
int t = r;
for (int i = r; i < n; ++i)
if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
// 如果绝对值最大的都等于0 说明这列不需要处理 就不要操作了
if (fabs(a[t][c]) < eps) continue;
// 把它交换到最顶上去 即交换第r行的元素和第t行的元素
for (int j = c; j <= n; ++j) swap(a[r][j], a[t][j]);
// 把它的(r, c)位置变1(除a[r][c])，其他位置元素跟着变
for (int j = n; j >= c; --j) a[r][j] /= a[r][c];
// 把底下那些行的第c列的元素都消成0 这一行的其他元素跟着变
// 其实就是a[i][j] -= a[r][j] * a[i][c]
for (int i = r + 1; i < n; ++i)
{
// 若a[i][c]是0 则已经处理好了 不需要操作了 不为零才需要操作
if (fabs(a[i][c]) > eps)
{
for (int j = n; j >= c; --j)
{
a[i][j] -= a[r][j] * a[i][c];
}
}
}
// 更新一下最顶上一行
++r;
}
// 若r < n 说明不是完美的阶梯型 对应无解和有无穷多解的情况
if (r < n)
{
// r及其往下的都是系数是0的方程
// 如果出现了0 = 非0 则说明有矛盾 无解
// 未出现则说明有无穷多解
// 遍历a[i][n]
for (int i = r; i < n; ++i)
{
// 无解
if (fabs(a[i][n]) > eps) return 2;
}
// 无穷多解
return 1;
}
// 有唯一解则把这个解解出 从第i = n - 1个方程开始
// 减去 列j = [i + 1, n - 1]的系数a[i][j] * (乘以它们的b) a[j][n]
for (int i = n - 1; i >= 0; --i)
{
for (int j = i + 1; j < n; ++j)
{
a[i][n] -= a[i][j] * a[j][n];
}
}
// 唯一解
return 0;
}
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
for (int j = 0; j <= n; ++j)
cin >> a[i][j];
int t = gauss();
// 有解 解就是(i, n)上面那些
if (t == 0)
{
for (int i = 0; i < n; ++i)
{
// 去掉-0.0
if (fabs(a[i][n]) < eps) a[i][n] = 0.0;
printf("%.2lfn", a[i][n]);
}
}
// 返回1表示有无穷多解
else if (t == 1)
{
puts("Infinite group solutions");
}
// 返回2则说明无解
else
{
puts("No solution");
}
return 0;
}
II 高斯消元法解异或线性方程组
异或运算又称为不进位加法，可以把异或方程组看成一个线性方程组来求解。
与高斯消元法类似，步骤为：
- 消成上三角矩阵；
- 判断：完美上三角矩阵（唯一解）、有矛盾（无解）、无矛盾（无穷多解）
怎么消成上三角矩阵？
- 枚举列
- 先找非零行
- 把非零行交换到最上面
- 用这个非零行把下面消0（异或一下就可以了）
代码：
#include <iostream>
using namespace std;
const int N = 110;
int a[N][N];
int n;
int gauss()
{
int r, c;
// 遍历每一列
for (r = 0, c = 0; c < n; ++c)
{
// 找到第一个非零行
int t = r;
for (int i = r; i < n; ++i)
{
if (a[i][c])
{
t = i;
break;
}
}
// 如果没有非零行 则continue
if (!a[t][c]) continue;
// 和第r行交换
for (int j = n; j >= c; --j) swap(a[r][j], a[t][j]);
// 把下面的行消成0
for (int i = r + 1; i < n; ++i)
{
// 如果不为0才消 消就是异或
if (a[i][c])
{
for (int j = n; j >= c; --j)
{
a[i][j] ^= a[r][j];
}
}
}
// 去下一行
++r;
}
if (r < n)
{
for (int i = r; i < n; ++i)
{
if (a[i][n]) return 2;
return 1;
}
}
// 唯一解 逆向求解
for (int i = n - 1; i >= 0; --i)
{
for (int j = i + 1; j < n; ++j)
{
// 如果a[i][j] 不为0才消 用&保证为0时异或0 不为0时异或a[j][n]
a[i][n] ^= a[i][j] & a[j][n];
}
}
return 0;
}
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
for (int j = 0; j <= n; ++j)
cin >> a[i][j];
int t = gauss();
if (t == 0)
{
for (int i = 0; i < n; ++i) cout << a[i][n] << endl;
}
else if (t == 1) puts("Multiple sets of solutions");
else puts("No solution");
return 0;
}
二、求组合数
1 递推预处理求组合数——N^2
数据范围：Cab, 1<=b<=a<=2000
如果直接使用组合数定义暴力计算，我们每算一个组合数就要做2000次循环，n个组合数一共进行20000000次运算，显然超时。
a和b的范围是2000，所有(a,b)的对数最多只有4000000对，我们可以先预处理出来所有它的值。
注意到，组合数有递推式：
C
a
b
=
C
a
−
1
b
+
C
a
−
1
b
−
1
C_a^{b} = C_{a - 1}^b + C_{a - 1}^{b - 1}
Cab=Ca−1b+Ca−1b−1
用4000000的时间复杂度先预处理出所有Cab的值即可。
这个公式的理解是：从a个东西中选出b的方法数，等于对一个物品，若我确定选它，则只需要在a - 1个物品中选b - 1个物品；若我确定不选它，那么只需要在a - 1个物品中选b个物品，两个加和即可，这个思想，和dp的思想一样。
#include <iostream>
using namespace std;
int n;
const int N = 2010;
const int mod = 1e9 + 7;
int C[N][N];
int main()
{
cin >> n;
for (int i = 0; i < N; ++i)
for (int j = 0; j <= i; ++j)
if (!j) C[i][j] = 1;
else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
int a, b;
while (n--)
{
scanf("%d %d", &a, &b);
printf("%dn", C[a][b]);
}
return 0;
}
2 预处理阶乘求组合数——NLOGN
数据范围：1<=b<=a<=1e5
本题的1 < b <= a <- 10^5，如果用dp直接处理Cab的值一定会超时，但是此时n的范围是1~1e4,所以我们可以用fact[i] = i! % mod，这样来预处理，这样就得到了分子。
因
为
a
b
%
p
!
=
a
%
p
b
%
p
,
所
以
分
母
不
能
这
么
处
理
.
因为frac{a}{b}%p!=frac{a%p}{b%p},所以分母不能这么处理.
因为ba%p!=b%pa%p,所以分母不能这么处理.
我们之前学习数论时，有学过处理取模意义下的逆元的计算，把除法换成乘法就好了。
据此，我们可以再预处理一个infact[i]，infact[i] = (i!)^(-1) % p的结果。
所以
C
a
b
=
f
a
c
t
[
a
]
∗
i
n
f
a
c
t
[
b
]
∗
i
n
f
a
c
t
[
a
−
b
]
C_a^b = fact[a] * infact[b]*infact[a - b]
Cab=fact[a]∗infact[b]∗infact[a−b]
阶乘的逆元也可以递推：
i
n
f
a
c
t
[
n
]
=
(
n
!
)
−
1
=
(
n
∗
(
n
−
1
)
!
)
−
1
=
n
−
1
∗
(
(
n
−
1
)
!
)
−
1
=
i
n
f
a
c
t
[
n
−
1
]
∗
n
−
1
由
费
马
小
定
理
=
i
n
f
a
c
t
[
n
−
1
]
∗
n
m
o
d
−
2
infact[n] = (n!)^{-1} = (n*(n - 1)!)^{-1} = n^{-1} * ((n - 1)!)^{-1} = infact[n - 1] * n^{-1}\ 由费马小定理 = infact[n - 1] * n^{mod - 2}
infact[n]=(n!)−1=(n∗(n−1)!)−1=n−1∗((n−1)!)−1=infact[n−1]∗n−1由费马小定理=infact[n−1]∗nmod−2
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, mod = 1e9 + 7;
int fact[N], infact[N];
int quick_power(int base, int power, int p)
{
int res = 1;
while (power > 0)
{
if (power & 1)
{
power -= 1;
res = (LL)res * base % p;
}
base = (LL)base * base % p;
power >>= 1;
}
return res;
}
void init()
{
fact[0] = infact[0] = 1;
for (int i = 1; i < N; ++i)
{
fact[i] = (LL)fact[i - 1] * i % mod;
// 两个1e9数相乘不会溢出LL 三个则有可能
infact[i] = (LL)infact[i - 1] * quick_power(i, mod - 2, mod) % mod;
}
}
int main()
{
init();
int n;
cin >> n;
int a, b;
while (n--)
{
scanf("%d%d", &a, &b);
int ans = (LL)fact[a] * infact[b] % mod * infact[a - b] % mod;
printf("%dn", ans);
}
return 0;
}
3 卢卡斯(Lucas)定理—询问次数少，数据范围暴大
Lucas定理的内容：
C
a
b
≡
C
a
%
p
b
%
p
∗
C
a
/
p
b
/
p
(
m
o
d
p
)
C_{a}^{b} equiv C_{a%p}^{b%p} * C_{a/p}^{b/p} pmod{p}
Cab≡Ca%pb%p∗Ca/pb/p(modp)
#include <iostream>
using namespace std;
typedef long long LL;
int p;
int quick_power(int base, int power)
{
int res = 1;
while (power > 0)
{
if (power & 1)
{
power -= 1;
res = (LL)res * base % p;
}
base = (LL)base * base % p;
power >>= 1;
}
return res;
}
int C(int a, int b)
{
int res = 1;
for (int j = a, i = 1; i <= b; ++i, --j)
{
res = (LL)res * j % p;
// 因为除有整除问题 这里反正是取模 所以分开
// 用取模意义下的逆元替代
res = (LL)res * quick_power(i, p - 2) % p;
}
return res;
}
int lucas(LL a, LL b)
{
if (a < p && b < p) return C(a, b);
return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}
int main()
{
int n;
cin >> n;
LL a, b;
while (n--)
{
cin >> a >> b >> p;
cout << lucas(a, b) << endl;
}
return 0;
}
4 精确的计算组合数(非取模意义下)
如果实现高精度乘法和除法，那么速度会比较慢，我们考虑只实现高精度乘法。
C
a
b
=
a
!
b
!
(
a
−
b
)
!
=
p
1
a
1
∗
p
2
a
2
∗
.
.
.
∗
p
k
a
n
所
以
我
们
只
要
求
出
a
!
中
的
质
因
子
p
i
的
个
数
让
它
减
去
b
!
和
(
a
−
b
)
!
中
质
因
子
p
i
的
个
数
，
然
后
让
r
e
s
∗
=
p
i
(
这
个
数
)
即
可
C_a^b = frac{a!}{b!(a - b)!} = p_1^{a_1} * p_2^{a_2} * ...*p_k^{a_n}\ 所以我们只要求出a!中的质因子p_i的个数 让它减去b!和(a - b)!中质因子p_i的个数，然后让res *= p_i^{(这个数)}即可
Cab=b!(a−b)!a!=p1a1∗p2a2∗...∗pkan所以我们只要求出a!中的质因子pi的个数让它减去b!和(a−b)!中质因子pi的个数，然后让res∗=pi(这个数)即可
如何求得a!中p的个数呢？
=
a
/
p
+
a
/
p
2
+
a
/
p
3
+
.
.
.
+
(
直
到
p
n
>
a
)
原
理
就
是
先
找
1
a
中
p
的
倍
数
然
后
/
p
2
表
示
p
2
的
个
数
它
们
只
被
计
算
了
一
个
p
补
上
，
以
此
类
推
。
= a / p + a / p^2 + a / p^3 +...+(直到p^n>a)\ 原理就是先找1~a中p的倍数 然后/p^2表示p^2的个数 它们只被计算了一个p 补上，以此类推。
=a/p+a/p2+a/p3+...+(直到pn>a)原理就是先找1 a中p的倍数然后/p2表示p2的个数它们只被计算了一个p补上，以此类推。
- 第一步：筛1~5000内的素数；
- 第二步：求质因子的个数;
- 第三步：用高精度乘法得到结果
#include <iostream>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N];
int sz = 0;
bool st[N];
int cnt[N];// 存储每个质数的出现次数
// 线性筛法
void getprimes(int n)
{
for (int i = 2; i <= n; ++i)
{
if (!st[i]) primes[sz++] = i;
for (int j = 0; primes[j] <= n / i; ++j)
{
st[i * primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
// 获取n!中质数p的出现次数
int getnum(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
// 高精度乘法
vector<int> mul(const vector<int>& a, int b)
{
vector<int> c;
int i = 0, t = 0;
while (i < a.size() || t != 0)
{
t = (i < a.size() ? a[i] : 0) * b + t;
c.push_back(t % 10);
t /= 10;
++i;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main()
{
int a, b;
cin >> a >> b;
// 获得1~a的质数
getprimes(a);
// 获取每个质数在cab中的出现次数
for (int i = 0; i < sz; ++i)
{
int p = primes[i];
// 质数p的出现次数是a!中的次数减去b!中的次数再减去(a - b)!的p的次数
cnt[i] = getnum(a, p) - getnum(b, p) - getnum(a - b, p);
}
// 用高精度乘法把他们都乘起来
vector<int> ans(1, 1);
for (int i = 0; i < sz; ++i)// 枚举质因子
for (int j = 0; j < cnt[i]; ++j)// 枚举其出现次数
ans = mul(ans, primes[i]);// 高精度乘法乘起来
// 打印结果
for (int i = ans.size() - 1; i >= 0; --i) printf("%d", ans[i]);
puts("");
return 0;
}
板子：
#include <iostream>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N];
int sz = 0;
bool st[N];
int cnt[N];// 质数的个数
void getprimes(int n)
{
for (int i = 2; i <= n; ++i)
{
if (!st[i]) primes[sz++] = i;
for (int j = 0; primes[j] <= n / i; ++j)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int getpinfactn(int n, int p)
{
int res = 0;
while (n > 0)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(const vector<int>& a, int b)
{
vector<int> c;
int i = 0, t = 0;
while (i < a.size() || t != 0)
{
t = (i < a.size() ? a[i] : 0) * b + t;
c.push_back(t % 10);
t /= 10;
++i;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
vector<int> combinnum(int a, int b)
{
getprimes(a);
for (int i = 0; i < sz; ++i)
{
int p = primes[i];
cnt[i] = getpinfactn(a, p) - getpinfactn(b, p) - getpinfactn(a - b, p);
}
vector<int> ans(1, 1);
for (int i = 0; i < sz; ++i)
for (int j = 0; j < cnt[i]; ++j)
ans = mul(ans, primes[i]);
return ans;
}
三、卡特兰数
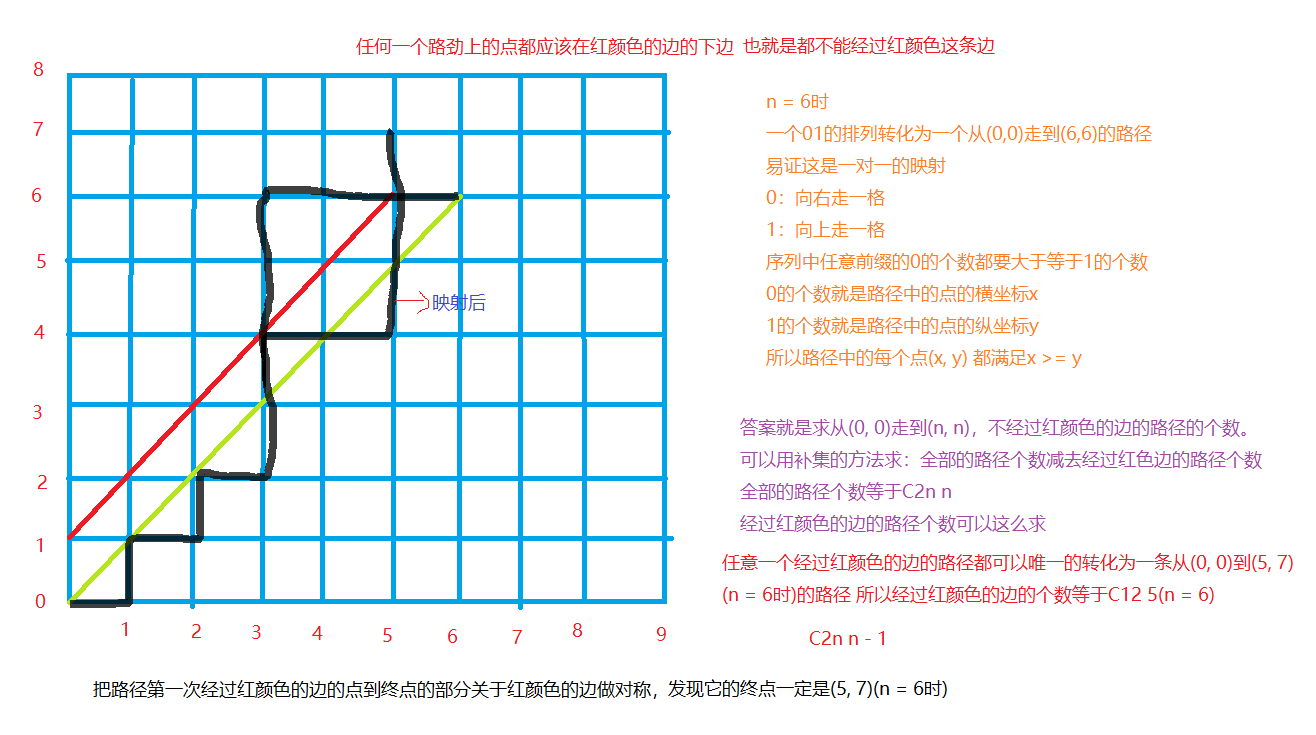$$ C_{2n}^n-C_{2n}^{n - 1} = frac{(2n)!}{n!n!} - frac{(2n)!}{(n - 1)!(n + 1)! } \= frac{(2n)!(n+1)-(2n)!n}{(n + 1)!n!}=frac{(2n)!}{(n + 1)!n!} = frac{1}{n + 1}frac{(2n)!}{n!n!}\=frac{1}{n + 1}C_{2n}^n $$ 这个数我们称为卡特兰数！很多问题的方案数都是卡特兰数，合法的括号（只有一种括号）的数目就是卡特兰数。
#include <iostream>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
// 快速幂 用来求%mod意义下的逆元
int quick_power(int base, int power)
{
int res = 1;
while (power)
{
if (power & 1)
{
res = (LL)res * base % mod;
power--;
}
base = (LL)base * base % mod;
power >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
int a = 2 * n, b = n;
int res = 1;
// 求的就是卡罗兰数 1/(n + 1) C2n n
for (int i = 1, j = a; i <= b; ++i, --j)
{
res = (LL)res * j % mod;
res = (LL)res * quick_power(i, mod - 2) % mod;
}
res = (LL)res * quick_power(n + 1, mod - 2) % mod;
cout << res << endl;
return 0;
}
最后
以上就是朴素荷花为你收集整理的算法中的数学知识(二)—高斯消元法、求组合数的四种方法、卡特兰数一、高斯消元法二、求组合数三、卡特兰数的全部内容，希望文章能够帮你解决算法中的数学知识(二)—高斯消元法、求组合数的四种方法、卡特兰数一、高斯消元法二、求组合数三、卡特兰数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复