Chapter-2 低速非结构化场景中的单一车辆决策与规划方法

本章介绍在低速非结构化场景中的最优化规划问题的构建和决策规划的计算流程。作者着重介绍了最优控制问题的一般形式和数值求解方法，以及使用A*求解初始值。

最优化问题为连续Bolza型问题，通过离散化通过非线性求解器计算。由于初始解既可以提高非线性规划问题的求解效率，又可以避免非线性规划限于局部最优解，因此先使用全局规划方法得到粗糙的轨迹作为决策轨迹，并作为非线性规划的初始解，非线性规划的结果最为最终规划的轨迹。

1. 轨迹规划命题的构建

车辆的轨迹规划任务是指在车辆的起始运动状态与终止时刻运动状态之间计算出满足符合约束调节的行驶轨迹，其中约束条件主要包括车辆内在的运动能力限制以及与外部环境相关的碰撞躲避限制。另一方面，满足上述约束条件的轨迹往往不止一条，应通过某一指标筛选优质的轨迹作为最终结果。鉴于轨迹规划任务存在硬约束条件以及用于寻优的指标式，因此适合采用最优控制问题的形式来描述。采用Bolza型最优控制问题形式。

$$J=\Phi (x(0),x(t_f),t_f)+{\int }_0^{t_f}L(x(t),u(t),t)dt\text{\hspace{1em}(1-1)}$$

其中，约束条件有：

• 系统动态方程约束；
• 两点边值约束；
• 流形约束(状态变量约束、控制变量约束、碰撞躲避约束)；

比如在泊车轨迹规划中，对终止时刻的车辆姿态角$\theta (t_f)$的边界值约束要格外慎重的设置。如果明确要求车辆在终止时刻到达某一既定姿态角${\theta }_f$，一般我们不会直接建立约束为$\theta (t_f)={\theta }_f$，而是：
$$\begin{gathered} \sin (\theta (t_f))=\sin ({\theta }_f) \\ \cos (\theta (t_f))=\cos ({\theta }_f) \\ \text{\hspace{1em}(1-2)} \end{gathered}$$
因为状态变量$\theta$可以被微分，因此$\theta (t)$一定是连续变量，在同样的初始时刻状态下，与${\theta }_f=0$相比，${\theta }_f=2\pi$意味着车辆在运动时域内要额外按逆时针方向绕行一圈。在充斥着障碍物的复杂场景中，我们一般无法提前预判车辆以何种“转圈”方式抵达终点。

在自动驾驶轨迹规划具体任务中，NLP问题的初始化是NLP求解的重要前置环节，将优质初始解的估算定义为轨迹决策。

2. 决策轨迹的生成

轨迹决策负责对场景所有的运动或者静止障碍物提供绕行方式的决策，其输出是一条衔接起点和终点的粗糙轨迹。路径信息反应了车辆在哪一侧绕行静态障碍物，沿路径行驶的时间信息决定以何种速度沿着该路径行驶，不同的时间戳布置可以造成针对移动障碍物的减速让行或者加速超车决策。除了一次生成粗略轨迹外，工程中也会解耦为路径决策+速度决策两个步骤。分开决策可以更直观、更有针对性地实现对车辆决策规划的调控，但会损害决策结果的最优性。

2.1 基于X-Y空间的搜索

在使用仅具备局部寻优能力的主流优化器求解轨迹规划问题时，最终收敛到的局部最优解与初始解保持同伦关系，因此初始解决定优化器是否可以收敛的全局最优解。因此具有全局优化搜索能力的A*算法可以被用来计算初始解。

此外，混合A*算法在离散$x-y-\theta$状态空间中使用A*策略并融合Reeds-Shepp曲线，与A*相比有以下差异：

• 混合A*算法更改了连通图的构建方式，混合A*算法是三个维度的；
• 混合A*算法更改了节点的拓展方式，$v$和$\delta$是按固定值离散来计算车辆状态的，也使混合A*算法不再具备完备性；
• 混合A*算法新增了节点的属性类别，每个节点会记录该节点的状态值和输入控制量；
• 混合A*算法变更了搜索策略，引入了RS曲线，可以满足终止位姿的精度，并且削弱使用控制采样带来的非完备性；
• 混合A*算法更改了节点碰撞检测的方式；
• 混合A*算法更改了启发函数的定义；

$$\begin{gathered} h=max(h_{nonholonomics},h_{collision-avoidance}) \\ {h}_{nonholonomics}=h_{RS},h_{collision-avoidance}=max(h_{A\ast },h_{Manhattan})\text{\hspace{1em}(2-1)} \end{gathered}$$

• 混合A*算法更改了函数g的定义；

2.2 基于S-T图的搜索

速度决策相当于在S-T图中搜索一条从原点(0,0)运动值($t_{end},s_{end}$)的路径，A*无疑可以胜任这一搜索任务，但需要做细微改动：

• 更改节点拓展方式，由于受到了S-T实际的意义限制，即时间只能向前流逝，可拓展区域减少至5块，甚至是3块。

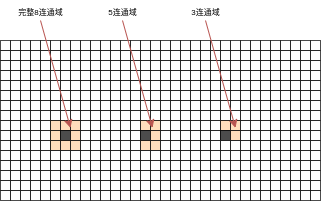
• 更改了函数g的定义：对垂直于父节点向上或者向下拓展的子节点施加额外的惩罚，是因为他们对应着行驶速率趋于无穷，是不合理的。

Apollo中的使用DP算法到达同样的目的，但是Apollo并未要求到达($t_{end},s_{end}$)状态。

2.3 X-Y-T三维A*算法

为了描述动态及静态障碍物，将时间轴视为运动状态，从而将移动障碍物统一记录在X-Y-T三维状态空间中中，此时静止障碍物对应着以其足迹为基本形状、以T轴上一段时间区间长度为高的直立柱状体，移动障碍物对应着倾斜的柱状体。

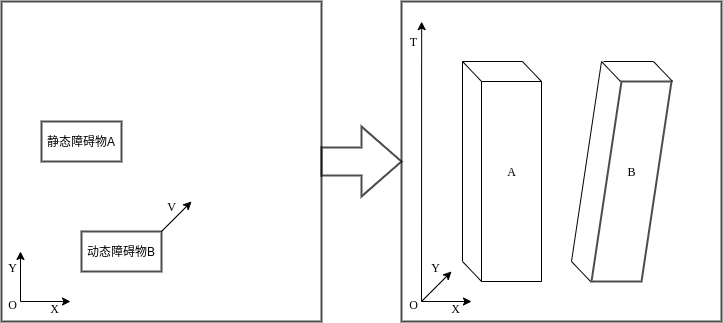
此外，为了提高A*的容错搜索能力，当搜索最终失败时返回当前已搜索过的"以最大程度抵近终点"的轨迹。

3. 轨迹生成

在得到决策轨迹后，可以使用决策轨迹来确定需要关心的部分障碍物，据此可以放心的忽略掉其他距离决策轨迹较远的障碍物而不影响可行性与最优性。可以沿着粗略轨迹铺设一条“绿色通道”，它能够天然地隔开可行驶区域与障碍物，可以将碰撞躲避约束条件等价的描述为车辆在通道中行驶的条件，使碰撞躲避约束条件转化为规模相对固定的条件，从而有效提升求解效率。这一部分，作者并未展开讲解，其发表的相关文章为：Fast Trajectory Planning for Off-Road Autonomous Driving with a Spatiotemporal Tunnel and Numerical Optimal Control Approach。

最后

以上就是冷酷黄蜂为你收集整理的Chapter-2 低速非结构化场景中的单一车辆决策与规划方法的全部内容，希望文章能够帮你解决Chapter-2 低速非结构化场景中的单一车辆决策与规划方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。