最近学习经典的计算流体力学入门书籍《计算流体力学基础及应用（约翰D安德森）》，跟着作者给出的过程写了计算程序，程序写的比较初级。

问题之 亚声速一超声速等熵喷管流动的CFD解法

问题的提法见《计算流体力学基础及应用（约翰D安德森）》中的7.3节，下面直接给出写的程序。

初始化参数

%亚声速-超声速等熵喷管流动CFD解法，拉瓦尔喷管 守恒形式方程解法 
%MacCormack方法 预估-校正 具有二阶精度
%初始参数（无量纲）
clc;clear;clf
x=0:0.1:3;
gm=1.4;%比热比
C=0.5;%科朗数
N=length(x);%节点数量
A=1+2.2.*(x-1.5).^2;%截面函数
rho=[ones(1,6),1.0-0.366.*(x(7:16)-0.5),0.634-0.3879.*(x(17:31)-1.5)];%密度
T=[ones(1,6),1.0-0.167.*(x(7:16)-0.5),0.833-0.3507.*(x(17:31)-1.5)];%温度
U1=rho.*A;%控制方程因变量
U2=repmat(0.59,1,31);%控制方程因变量
V=U2./U1;%速度
U3=U1.*(T./(gm-1)+gm/2.*V.^2);%控制方程因变量
U1_t=zeros(1,N);%因变量1一阶偏导
U1_mid=U1;%预估步因变量1
U1_tt=zeros(1,N);%校正步因变量1
U1_av=zeros(1,N);%校正因变量1
U2_t=zeros(1,N);%因变量2一阶偏导
U2_mid=U2;%预估步因变量2
U2_tt=zeros(1,N);%校正步因变量2
U2_av=zeros(1,N);%校正因变量1
U3_t=zeros(1,N);%因变量3一阶偏导
U3_mid=U3;%预估步因变量2
U3_tt=zeros(1,N);%校正步因变量3
U3_av=zeros(1,N);%校正因变量1
F1=U2;%通量1
F1_mid=U2;%预估步通量1初始化
F2=U2.^2./U1+(gm-1)/gm.*(U3-gm/2.*U2.^2./U1);%通量2
F2_mid=U2.^2./U1+(gm-1)/gm.*(U3-gm/2.*U2.^2./U1);%预估步通量2初始化
F3=gm.*U2.*U3./U1-gm*(gm-1)/2.*U2.^3./U1.^2;%通量3
F3_mid=gm.*U2.*U3./U1-gm*(gm-1)/2.*U2.^3./U1.^2;%预估步通量3初始化
J2=zeros(1,N);%源项2
J2_mid=zeros(1,N);%预估步源项2初始化
rho_mid=zeros(1,N);%密度预估值
T_mid=zeros(1,N);%温度预估值
t=zeros(1,N);%局部步长
k=0;%迭代次数初始化
k0=2000;%指定迭代次数

迭代过程

%迭代过程
while 1
    k=k+1;
% 计算预估步 向前差分
for i=1:N
    t(i)=C.*0.1./(V(i)+sqrt(T(i)));%计算满足稳定性条件的各个局部步长
end
delta_t=min(t);%取最小步长
for i=2:N-1
    J2(i)=1/gm.*rho(i).*T(i).*(A(i+1)-A(i))/0.1;%预估步源项2
    U1_t(i)=-(F1(i+1)-F1(i))/0.1;%计算因变量1一阶偏导
    U2_t(i)=-(F2(i+1)-F2(i))/0.1+J2(i);%计算因变量2一阶偏导
    U3_t(i)=-(F3(i+1)-F3(i))/0.1;%计算因变量3一阶偏导;
    U1_mid(i)=U1(i)+U1_t(i).*delta_t;%因变量1预估
    U2_mid(i)=U2(i)+U2_t(i).*delta_t;%因变量2预估
    U3_mid(i)=U3(i)+U3_t(i).*delta_t;%因变量3预估
    rho_mid(i)=U1_mid(i)./A(i);%密度预估
    T_mid(i)=(gm-1).*(U3_mid(i)./U1_mid(i)-gm/2.*U2_mid(i).^2./U1_mid(i).^2);%温度预估
    F1_mid(i)=U2_mid(i);%预估步通量1
    F2_mid(i)=U2_mid(i).^2/U1_mid(i)+(gm-1)/gm.*(U3_mid(i)- ...
        gm/2.*U2_mid(i).^2./U1_mid(i));%预估步通量2
    F3_mid(i)=gm.*U2_mid(i).*U3_mid(i)./U1_mid(i)-gm*(gm-1)/ ...
        2.*U2_mid(i).^3./U1_mid(i).^2;%预估步通量3
end
U2_mid(1)=2.*U2_mid(2)-U2_mid(3);%入口点1处通过点2 3的插值获得
rho_mid(1)=U1_mid(1)./A(1);
V_mid(1)=U2_mid(1)./U1_mid(1);
U3_mid(1)=U1_mid(1)*(1/(gm-1)+gm/2*V_mid(1)^2);
F1_mid(1)=U2_mid(1);
F2_mid(1)=U2_mid(1).^2./U1_mid(1)+(gm-1)/gm.*(U3_mid(1)-gm/2.*U2_mid(1).^2./U1_mid(1));
F3_mid(1)=gm.*U2_mid(1).*U3_mid(1)./U1_mid(1)-gm*(gm-1)/2.*U2_mid(1).^3./U1_mid(1).^2;
%计算校正步 向后差分
for i=2:N-1
    J2_mid(i)=1/gm.*rho_mid(i).*T_mid(i).*(A(i)-A(i-1))/0.1;%校正步源项2
    U1_tt(i)=-(F1_mid(i)-F1_mid(i-1))/0.1;%计算因变量1一阶偏导
    U2_tt(i)=-(F2_mid(i)-F2_mid(i-1))/0.1+J2_mid(i);%计算因变量2一阶偏导
    U3_tt(i)=-(F3_mid(i)-F3_mid(i-1))/0.1;%计算因变量3一阶偏导;
    U1_av(i)=0.5.*(U1_t(i)+U1_tt(i));%变量1校正
    U2_av(i)=0.5.*(U2_t(i)+U2_tt(i));%变量2校正
    U3_av(i)=0.5.*(U3_t(i)+U3_tt(i));%变量3校正
end
U1=U1+U1_av.*delta_t;%下一时间步
U1(N)=2.*U1(N-1)-U1(N-2);%出口处点N通过插值获得
U2=U2+U2_av.*delta_t;%下一时间步
U2(1)=2.*U2(2)-U2(3);%入口点1处通过点2 3的插值获得
U2(N)=2.*U2(N-1)-U2(N-2);%出口处点N通过插值获得
rho=U1./A;
V=U2./U1;
U3=U3+U3_av.*delta_t;%下一时间步
U3(1)=U1(1)*(1/(gm-1)+gm/2*V(1)^2);
U3(N)=2.*U3(N-1)-U3(N-2);%出口处点N通过插值获得
T=(gm-1).*(U3./U1-gm/2.*V.^2);
p=rho.*T;
Ma=V./sqrt(T);
F1=U2;%通量1
F2=U2.^2./U1+(gm-1)/gm.*(U3-gm/2.*U2.^2./U1);%通量2
F3=gm.*U2.*U3./U1-gm*(gm-1)/2.*U2.^3./U1.^2;%通量3
%喉道参数获取
rhot(k)=rho(16);
Vt(k)=V(16);
Tt(k)=T(16);
Mat(k)=Ma(16);
pt(k)=p(16);
re_rho(k)=abs(rho(16));
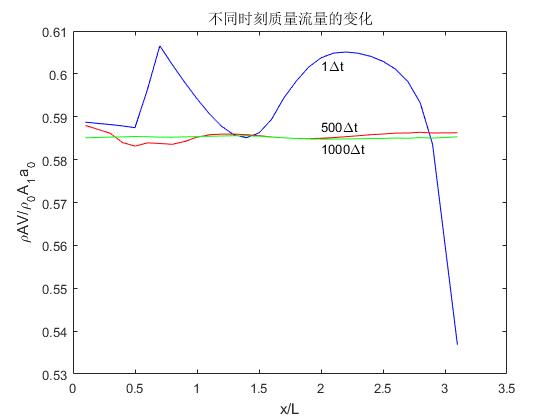
%绘制不同时间步质量流量变化
if k==1
    xtick=1:N;
    rhoAV=rho(xtick).*A(xtick).*V(xtick);
    plot(xtick/10,rhoAV,'-b')
    hold on
elseif k==500
    xtick=1:N;
    rhoAV=rho(xtick).*A(xtick).*V(xtick);
    plot(xtick/10,rhoAV,'-r')
    hold on
elseif k==1000
    xtick=1:N;
    rhoAV=rho(xtick).*A(xtick).*V(xtick);
    plot(xtick/10,rhoAV,'-g')
    xlabel('x/L'),ylabel('rhoAV/rho_0A_1a_0')
    title('不同时刻质量流量的变化')
    text(2,rhoAV(N)-0.0025,'1000Deltat')
    text(2,rhoAV(N)+0.0025,'500Deltat')
    text(2,0.602,'1Deltat')
    hold on
else
    
end
%迭代次数
if k==k0
    break;
else
    
end
end

绘图

figure
x0=1:1:k;%时间步
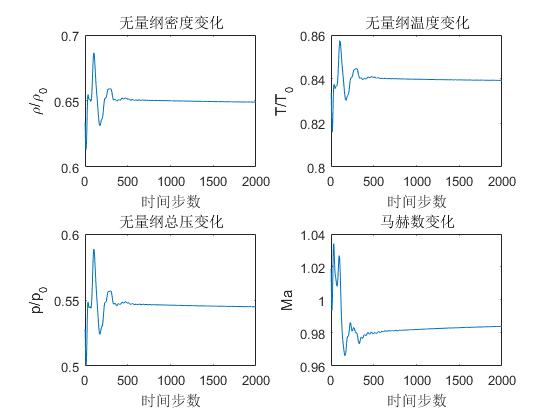
%绘制密度-时间步图像
rho_change=rhot(x0);
subplot(2,2,1),plot(x0,rho_change)
ylabel('rho/rho_0'),xlabel('时间步数')
title('无量纲密度变化')
%绘制温度-时间步图像
T_change=Tt(x0);
subplot(2,2,2),plot(x0,T_change)
ylabel('T/T_0'),xlabel('时间步数')
title('无量纲温度变化')
%绘制压力-时间步图像
p_change=pt(x0);
subplot(2,2,3),plot(x0,p_change)
ylabel('p/p_0'),xlabel('时间步数')
title('无量纲总压变化')
%绘制马赫数-时间步图像
Ma_change=Mat(x0);
subplot(2,2,4),plot(x0,Ma_change)
ylabel('Ma'),xlabel('时间步数')
title('马赫数变化')
fprintf('迭代最终结果:n密度rho=%6.4en温度T=%6.4en速度V=%6.4en总压p=%6.4en马赫数Ma=%6.4en' ...
    ,rhot(k),Tt(k),pt(k),Vt(k),Mat(k))
figure 
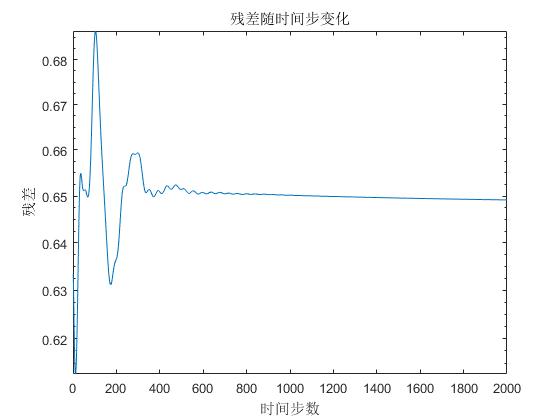
re_rho_change=re_rho(x0);
semilogy(x0,re_rho_change)
ylabel('残差'),xlabel('时间步数')
title('残差随时间步变化')
x00=1:1:N;
figure
p0=p(x00);
subplot(2,2,1)
plot(x00/10,p0)
ylabel('p/p_0'),xlabel('x/L')
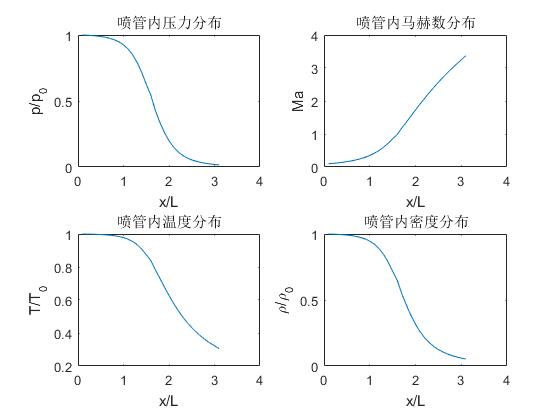
title('喷管内压力分布')
Ma0=Ma(x00);
subplot(2,2,2)
plot(x00/10,Ma0)
ylabel('Ma'),xlabel('x/L')
title('喷管内马赫数分布')
T0=T(x00);
subplot(2,2,3)
plot(x00/10,T0)
ylabel('T/T_0'),xlabel('x/L')
title('喷管内温度分布')
rho0=rho(x00);
subplot(2,2,4)
plot(x00/10,rho0)
ylabel('rho/rho_0'),xlabel('x/L')
title('喷管内密度分布')

结果

迭代最终结果:
密度rho=6.4917e-01
温度T=8.3937e-01
速度V=5.4489e-01
总压p=9.0153e-01
马赫数Ma=9.8401e-01

最后

以上就是明理蜻蜓为你收集整理的Matlab 编程 《计算流体力学基础及应用（约翰D安德森）》 亚声速-超声速等熵喷管流动CFD解法 拉瓦尔喷管 守恒形式方程解法问题之 亚声速一超声速等熵喷管流动的CFD解法的全部内容，希望文章能够帮你解决Matlab 编程 《计算流体力学基础及应用（约翰D安德森）》 亚声速-超声速等熵喷管流动CFD解法 拉瓦尔喷管 守恒形式方程解法问题之 亚声速一超声速等熵喷管流动的CFD解法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。