神经网络的正向传递与反向传播

1.单个神经元

神经网络是由一系列神经元组成的模型，每一个神经元实际上做得事情就是实现非线性变换。

如下图就是一个神经元的结构：

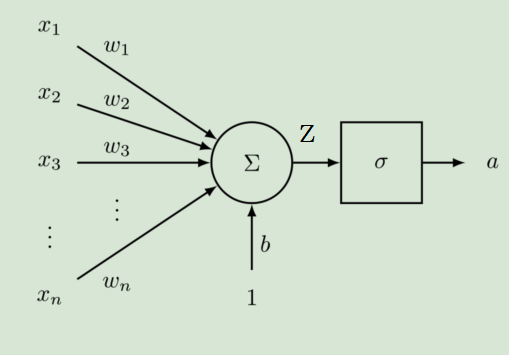
神经元将两个部分：上一层的输出 $(x_1,x_2...,x_n)$与权重$(w_1,w_2...,w_n)$ 对应相乘相加，然后再加上一个偏置 $b$ 之后的值经过激活函数处理后完成非线性变换。

记 $z=w\cdot x+b$，$a=\sigma (z)$，则 $z$ 是神经元非线性变换之前的结果，这部分仅仅是一个简单的线性函数。$\sigma$是Sigmod激活函数，该函数可以将无穷区间内的数映射到(-1,1)的范围内。$a$ 是神经元将 $z$ 进行非线性变换之后的结果。

Sigmod函数图像如下图：
$$sigmod(x)=\frac{1}{1+e^{-x}}$$

因此，结果 $a$ 就等于：
$$a=\frac{1}{1+e^{-(w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b)}}$$

这里再强调一遍，神经元的本质就是做非线性变换。

2.由神经元组成的神经网络

神经元可以理解成一个函数，神经网络就是由很多个非线性变换的神经元组成的模型，因此神经网络可以理解成是一个非常复杂的复合函数。

对于上图中的网络：

• $(x_1,x_2,...,x_n)$ 为 $n$ 维输入向量。
• $W_{ij}$，表示后一层第$i$个神经元与前一层第$j$个神经元之间的权值。
• $z=Wx+b$，是没有经过激活函数非线性变换之前的结果。
• $a=\sigma (z)$，是 $z$ 经过激活函数非线性变换之后的结果。
• $s=U^{T}a$，为网络最终的输出结果。

3.目标函数

以折页损失为目标函数：
$$minmizeJ=max(\Delta +s_c-s,0)$$

其中 $s_c=U^T\sigma (W{x}_c+b)，s=U^T\sigma (Wx+b)$。一般可以把 Δ 固定下来，比如设为1或者10。

一般来说，学习算法的学习过程就是优化调整参数，使得损失函数，或者说预测结果和实际结果的误差减小。BP算法其实是一个双向算法，包含两个步骤：

• 1.正向传递输入信息，得到 $Loss$ 值。
• 2.反向传播误差，从而由优化算法来调整网络权值。

4.求解损失函数对某个权值的梯度

对于上面的图，假设图中指示出的网络中的某个权值 $w_{jk}^l$ 发生了一个小的改变 $\Delta w_{jk}^l$ ，假设网络最终损失函数的输出为 $C$ ，则 $C$ 应该是关于 $w_{jk}^l$ 的一个复合函数。

所谓复合函数，就是把 $C$ 看成因变量，则$w_{jk}^l$ 可以看成是导致 $C$ 改变的自变量，比如假设有一个复合函数 $y=f(g(x))$，则 $y$ 就好比这里的$C$ ，$x$ 就好比$w_{jk}^l$，$w_{jk}^l$ 每经过一层网络可以看成是经过某个函数的处理 。而下面求导的时候都用偏导数，是因为虽然我们这里只关注了一个 $w_{jk}^l$，但是实际上网络中的每一个 $w$ 都可以看成一个 $x$。

显然，这个 $\Delta w_{jk}^l$ 的变化会引起下一层直接与其相连的一个神经元，以及下一层之后所有神经元直到最终输出 $C$ 的变化，如图中蓝线标记的就是该权值变化的影响传播路径。

把 $C$ 的改变记为 $\Delta C$，则根据高等数学中导数的知识可以得到：
$$\Delta C\approx \frac{\partial C}{\partial w_{jk}^l}\Delta w_{jk}^l\text{\hspace{1em}(1)}$$

同样的道理可以得到上图中与 $w_{jk}^l$ 直接相连的神经元 $a_j^l$ 发生的变化 $\Delta a_j^l$ ：
$$\Delta a_j^l\approx \frac{\partial a_j^l}{\partial w_{jk}^l}\Delta w_{jk}^l\text{\hspace{1em}(2)}$$

则神经元 $a_j^l$ 下面一层第 $q$ 个与其相连的神经元 $a_q^{l+1}$ 的变化为：
$$\Delta a_q^{l+1}\approx \frac{\partial a_q^{l+1}}{\partial a_j^l}\Delta a_j^l\text{\hspace{1em}(3)}$$

将 $(2)$ 代入 $(3)$ 可以得到：
$$\Delta a_q^{l+1}\approx \frac{\partial a_q^{l+1}}{\partial a_j^l}\frac{\partial a_j^l}{\partial w_{jk}^l}\Delta w_{jk}^l\text{\hspace{1em}(4)}$$

假设从 $a_j^l$ 到 $C$的一条路径为$a_j^l,a_q^{l+1},...,a_n^{L-1},a_m^L$，则在该条路径上 $C$ 的变化量 $\Delta C$ 为：
$$\Delta C\approx \frac{\partial C}{\partial a_m^L}\frac{\partial a_m^L}{\partial a_n^{L-1}}\frac{\partial a_n^{L-1}}{\partial a_p^{L-2}}...\frac{\partial a_q^{l+1}}{\partial a_j^l}\frac{\partial a_j^l}{\partial w_{jk}^l}\Delta w_{jk}^l\text{\hspace{1em}(5)}$$

至此，我们已经得到了一条路径上的变化量，其实本质就是链式求导法则，或者说是复合函数求导法则。那么整个的变化量就是把所有可能链路上的变化量加起来：
$$\Delta C\approx \sum _{mnp...q}\frac{\partial C}{\partial a_m^L}\frac{\partial a_m^L}{\partial a_n^{L-1}}\frac{\partial a_n^{L-1}}{\partial a_p^{L-2}}...\frac{\partial a_q^{l+1}}{\partial a_j^l}\frac{\partial a_j^l}{\partial w_{jk}^l}\Delta w_{jk}^l\text{\hspace{1em}(6)}$$
则 $C$ 对某个权值 $w_{jk}^l$ 的梯度为：
$$\frac{\partial C}{\partial w_{jk}^l}\approx \sum _{mnp...q}\frac{\partial C}{\partial a_m^L}\frac{\partial a_m^L}{\partial a_n^{L-1}}\frac{\partial a_n^{L-1}}{\partial a_p^{L-2}}...\frac{\partial a_q^{l+1}}{\partial a_j^l}\frac{\partial a_j^l}{\partial w_{jk}^l}\text{\hspace{1em}(7)}$$

到这里从数学分析的角度来说，我们可以知道这个梯度是可以计算和求解的。

总结：

• 1.每两个神经元之间是由一条边连接的，这个边就是一个权重值，它是后一个神经元 $z$部分，也就是未经激活函数非线性变换之前的结果对前一个神经元的 $a$部分，也就是经激活函数非线性变换之后的结果的偏导数。
• 2.一条链路上所有偏导数的乘积就是这条路径的变化量。
• 3.所有路径变化量之和就是整个损失函数的变化量。

5.反向传播算法Backpropgation

5.1 明确一些定义

对于上面的神经网络，首先明确下面一些定义：

• $x_i$是网络的输入。
• $s$是网络的输出。
• $z_j^{(k)}$ 表示第 $k$ 层第 $j$ 个神经元在激活函数非线性变换之前的结果。
• $a_j^{(k)}$ 表示第 $k$ 层第 $j$ 个神经元在激活函数非线性变换之后的结果，也就是说$a_j^{(k)}=\sigma (z_j^{(k)})$。
• 对于输入层：$x_j=z_j^{(1)}=a_j^{(1)}$。
• $W_{ij}^{(l)}$，表示 $l+1$ 层第$i$个神经元与前一层第$j$个神经元之间的权值。

一个特别重要的定义：

• ${\delta }_j^{(k)}$是一个定义，这个定义指的是损失函数在$z_j^{(k)}$处的反向传播误差，即损失函数对$z_j^{(k)}$的梯度：${\delta }_j^{(k)}=\frac{\partial J}{\partial z_j^{(k)}}$，$J$ 为损失函数。这个定义在后面推导反向传播的时候会用到，每一处的 ${\delta }_j^{(k)}$都是通过后面的 $\delta$ 传递整合得到的，后面会具体分析整过程，这样的过程可以大大简化计算。

5.2 计算一个梯度

假设损失函数为：$J=(1+s_c-s)$。

来计算一下 $\frac{\partial J}{\partial W_{14}^{(1)}}$，由于 $s$ 是网络的输出，$\frac{\partial J}{\partial s}=-1$，所以只需要计算$\frac{\partial s}{\partial W_{14}^{(1)}}$即可。

而由于 $s$ 激活函数就是1，所以有：
$$s=a_1^{(3)}=z_1^{(3)}=W_{11}^{(2)}{a}_1^{(2)}+W_{12}^{(2)}{a}_2^{(2)}\text{\hspace{1em}(8)}$$

$$\frac{\partial s}{\partial W_{14}^{(1)}}=\frac{\partial (W_{11}^{(2)}{a}_1^{(2)}+W_{12}^{(2)}{a}_2^{(2)})}{\partial W_{14}^{(1)}}\text{\hspace{1em}(9)}$$

显然 $W_{14}^{(1)}$ 只会影响 $z_1^{(2)}$ 和 $a_1^{(2)}$，所以 $W_{12}^{(2)}{a}_2^{(2)}$对 $W_{14}^{(1)}$ 求偏导就是0，并且上面的网络可以简化成下面的图：

所以：
$$\frac{\partial s}{\partial W_{14}^{(1)}}=\frac{\partial W_{11}^{(2)}{a}_1^{(2)}}{\partial W_{14}^{(1)}}=W_{11}^{(2)}\frac{\partial a_1^{(2)}}{\partial W_{14}^{(1)}}\text{\hspace{1em}(9)}$$

由于 $a_1^{(2)}=\sigma (z_1^{(2)})$，$z_1^{(2)}=b_1^{(1)}+{\sum }_k{a}_k^{(1)}{W}_{1k}^{(1)}$，$\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}={\sigma }^{\prime }(z_1^{(2)})$，代入公式 $(9)$ 可以得到：
$$\begin{gathered} \frac{\partial s}{\partial W_{14}^{(1)}}=W_{11}^{(2)}\frac{\partial a_1^{(2)}}{\partial W_{14}^{(1)}}=W_{11}^{(2)}\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\frac{\partial z_1^{(2)}}{\partial W_{14}^{(1)}1} \\ =W_{11}^{(2)}{\sigma }^{\prime }(z_1^{(2)})\frac{\partial (b_1^{(1)}+{\sum }_k{a}_k^{(1)}{W}_{1k}^{(1)})}{\partial W_{14}^{(1)}}\text{\hspace{1em}(10)} \end{gathered}$$

公式 $(10)$ 中 $\frac{\partial (b_1^{(1)}+{\sum }_k{a}_k^{(1)}{W}_{1k}^{(1)})}{\partial W_{14}^{(1)}}=a_4^{(1)}$ 。

此外还有一个更重要的变换，同样的方法可以求出：
$$\frac{\partial J}{\partial z_1^{(2)}}=W_{11}^{(2)}{\sigma }^{\prime }(z_1^{(2)})$$

并且结合前面对 ${\delta }_j^{(k)}$ 的定义，公式 $(10)$ 可以写成:
$$\frac{\partial s}{\partial W_{14}^{(1)}}=\frac{\partial J}{\partial z_1^{(2)}}{a}_4^{(1)}={\delta }_1^{(2)}{a}_4^{(1)}\text{\hspace{1em}(11)}$$

所以损失函数对任意一个网络权值的梯度可以写成两个值相乘的形式。对于 $a_4^{(1)}$，它是网络前向传递过程中的一个神经元的输出，我们当然可以在网络前向传递的时候将它保存下来。而对于 ${\delta }_1^{(2)}$，它是反向传播过来的梯度，也就是 $J$ 对 $z$ 的梯度，下面来看如何通过后面神经元的 ${\delta }_i^{(k)}$ 反向传播得到 前一个神经元处的 ${\delta }_j^{(k-1)}$ 。

5.3 反向传播误差

到这里需要注意，反向传播仅指用于计算梯度的方法，它并不是用于神经网络的整个学习算法。通过反向传播算法算法得到梯度之后，可以使用比如随机梯度下降算法等来进行学习。

反向传播算法传播的是误差，传播方向是从最后一层依次往前，这是一个迭代的过程。在上面的过程中，我们求得了损失函数对于某个权值的梯度，通过该处的梯度值，可以将其向前传播，得到前一个结点的梯度。

例如对于上面的图，假设已经求出 $z_i^{(k)}$ 处的梯度${\delta }_i^{(k)}$，则将误差按照某条连接路径，传递到 $a_j^{(k-1)}$处，则该处的梯度为 ${\delta }_i^{(k)}{W}_{ij}^{(k-1)}$。

实际上这只是一条路径， $a_j^{(k-1)}$处可能会收到很多个不同的误差，例如下面该神经元后面有两条权值边的情况：

这个时候只要把它们相加就好了，所以 $a_j^{(k-1)}$处，则该处的梯度为 ${\sum }_i{\delta }_i^{(k)}{W}_{ij}^{(k-1)}$。

于是 $z_j^{(k-1)}$ 处的梯度 ${\delta }_j^{(k-1)}$ 就为 ${\sigma }^{\prime }(z_j^{(k-1)}){\sum }_i{\delta }_i^{(k)}{W}_{ij}^{(k-1)}$。

所以只要从网络的最后面开始，迭代上面的过程，就可以求出网络每个地方 $J$ 对 $z$ 梯度，从而求出 $J$ 对与 $z$相连的 $w$ 的梯度了。

6.优化示例

再次说一下，反向传播仅指用于计算梯度的方法，它并不是用于神经网络的整个学习算法。通过反向传播算法算法得到梯度之后，还需要使用比如随机梯度下降算法等来进行学习。

在上面的过程中，我们通过反向传播算法求解出了任意一个$z_j^{(i)}$ 处的梯度 ${\delta }_j^{(i)}$ ，为什么是 $z_j^{(i)}$ 而不是 $a_j^{(i)}$呢，因为 $z_j^{(i)}$前面就是连接它的 $w$,以随机梯度下降算法为例，$w$的优化方法为：
$$w_{ijnew}^{(l)}=w_{ijold}^{(l)}-\eta \cdot \frac{\partial J}{\partial w_{ij}^{(l)}}=w_{ijold}^{(l)}-\eta \cdot {\delta }_i^{(l+1)}\cdot a_j^{(l)}\text{\hspace{1em}(12)}$$

最后

以上就是难过帅哥最近收集整理的关于神经网络的正向传递与反向传播的全部内容，更多相关神经网络内容请搜索靠谱客的其他文章。