我们在上一节中已经很详细地学习了有关线性回归算法的推导过程,具体可点击此处阅读:https://blog.csdn.net/weixin_56197703/article/details/123141469
目录
一、简单线性回归:
1、正规方程实现:
2、sklearn算法实现:
二、二元一次方程线性回归:
1、正规方程实现:
2、sklearn算法实现:
然后我们这次就通过代码来实现线性回归:
一、简单线性回归: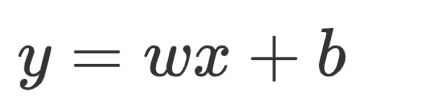
一元一次方程,在机器学习中一元表示一个特征,b表示截距,y表示目标值。
1、正规方程实现:
import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵,reshape
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
# 目标值y真实值!!!
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 重新构造X,b截距,相当于系数w0,前面统一乘以1
X = np.concatenate([X,np.full(shape = (30,1),fill_value= 1)],axis = 1)
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)
print('一元一次方程真实的斜率和截距是:',w, b)
print('通过正规方程求解的斜率和截距是:',θ)
# 根据求解的斜率和截距绘制线性回归线型图
plt.plot(X[:,0],X.dot(θ),color = 'green')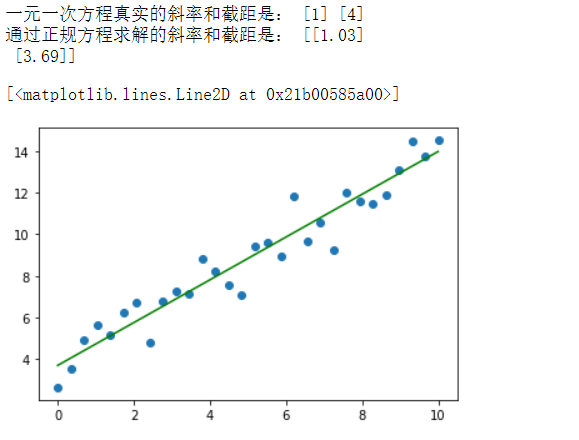
2、sklearn算法实现:
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 使用scikit-learn中的线性回归求解
model = LinearRegression()
model.fit(X,y)
w_ = model.coef_
b_ = model.intercept_
print('一元一次方程真实的斜率和截距是:',w, b)
print('通过scikit-learn求解的斜率和截距是:',w_,b_)
plt.plot(X,X.dot(w_) + b_,color = 'green')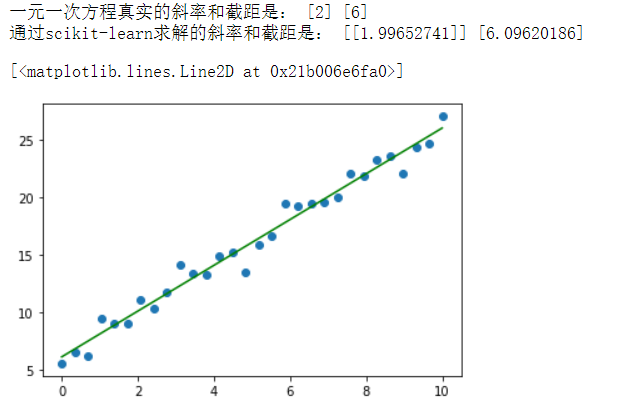
二、二元一次方程线性回归:
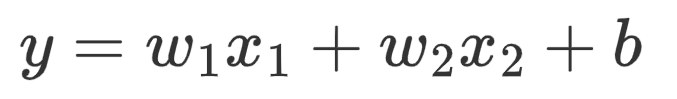
二元一次方程,x_1、x_2 相当于两个特征,b是方程截距
1、正规方程实现:
import numpy as np
import matplotlib.pyplot as plt
# from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = plt.subplot(111,projection = '3d')
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X,将x1、x2以及截距b,相当于系数w0,前面统一乘以1进行数据合并
X = np.concatenate([x1,x2,np.full(shape = (300,1),fill_value=1)],axis = 1)
w = np.concatenate([w,b])
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)
print('二元一次方程真实的斜率和截距是:',w)
print('通过正规方程求解的斜率和截距是:',θ.reshape(-1))
# # 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * θ[0] + y * θ[1] + θ[2]
ax.plot(x,y,z ,color = 'red')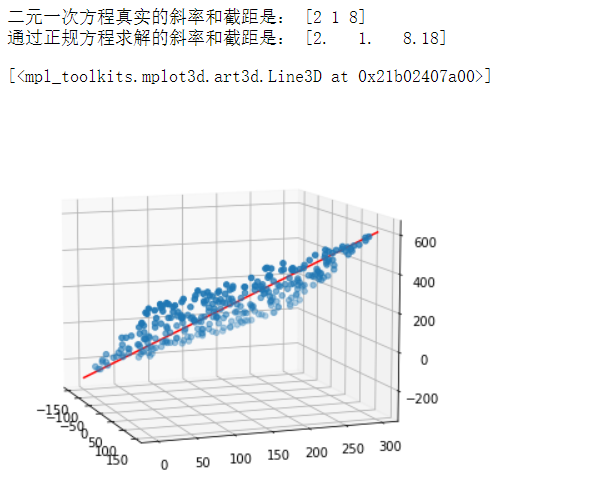
2、sklearn算法实现:
import numpy as np
import matplotlib.pyplot as plt
# from mpl_toolkits.mplot3d.axes3d import Axes3D
import warnings
warnings.filterwarnings('ignore')
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = plt.subplot(111,projection = '3d')
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X,将x1、x2以及截距b,相当于系数w0,前面统一乘以1进行数据合并
X = np.concatenate([x1,x2],axis = 1)
# 使用scikit-learn中的线性回归求解
model = LinearRegression()
model.fit(X,y)
w_ = model.coef_.reshape(-1)
b_ = model.intercept_
print('二元一次方程真实的斜率和截距是:',w,b)
print('通过scikit-learn求解的斜率和截距是:',w_,b_)
# # 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * w_[0] + y * w_[1] + b_
ax.plot(x,y,z ,color = 'green')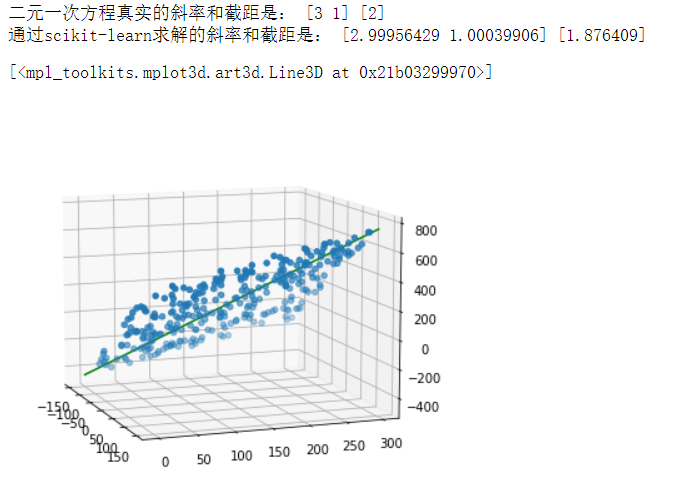
计算出的结果不一定是和真实值相同,只要模型结果与真实值够接近就行!!!
最后
以上就是无辜小土豆最近收集整理的关于机器学习5-线性回归算法的代码实现一、简单线性回归: 二、二元一次方程线性回归:的全部内容,更多相关机器学习5-线性回归算法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复