简介

十种常见的算法可以分为两种：

• 第一种是比较类排序，也成为线性排序，其时间复杂度不能超过O(nlogn)
• 第二种是非比较类排序，不通过比较来决定元素间的相对排序，时间复杂度可以超过O(nlogn)

那么各个方法的复杂度如下：

算法介绍

1. 冒泡排序

冒泡算法的思想是：

1. 指针从第一个数开始与其后面一个数进行比较
2. 如果后面一个数较大，则指针指向后面一个数；如果前面一个数较大，则两个数交换位置，指针指向大的数
3. 直到最大的数放到了最后一个位置，指针从头开始重复1，2步骤，最后直到遍历了n次（n为list的长度）

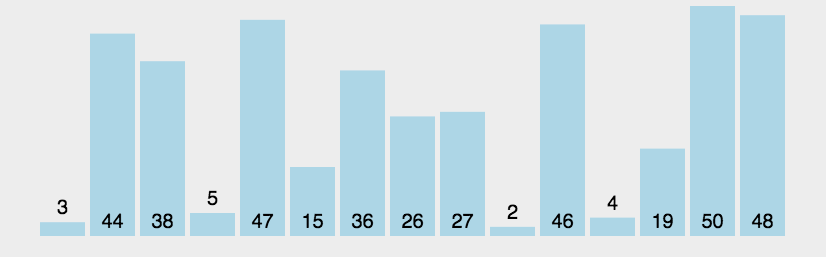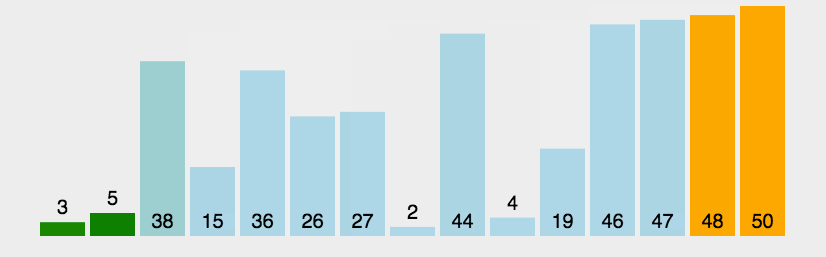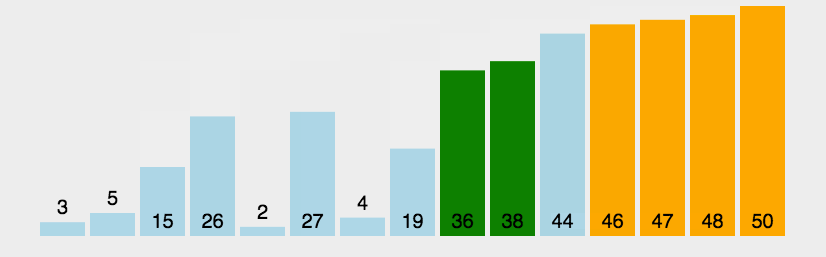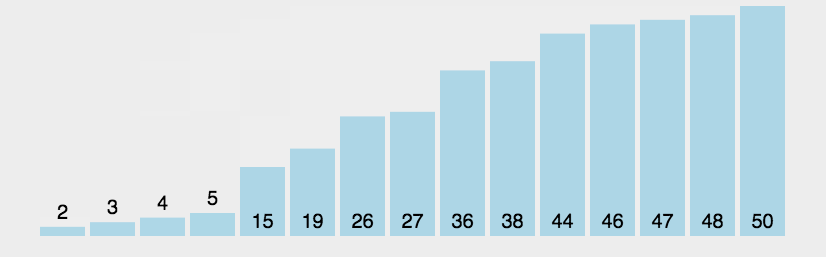
def BubbeSort(lst):
for i in range(len(lst)):
for j in range(0, len(lst)-i-1):
if lst[j] > lst[j+1]: #判断每一个数值与前面一个数值的大小
lst[j], lst[j+1] = lst[j+1], lst[j]
#如果前面的数值更大，那么与后面的数值交换位置
print(lst)
BubbeSort([4,3,2,1])

冒泡方法的时间复杂度最差为O($n^2$)，最好O($nlogn$)

2. 快速排序

快排最重要的思想就是***分治***， 大事化小，小事化无。这种思想意味这快排在处理大数据量的情况下更具有优势。快排的方法分以下几步：

1. 寻找基准值（可以选list的第一位，中间位，最后一位）
2. 比较list中的所，有值把小于基准值的放在基准值左侧，大于基准值的放在基准值的右侧
3. 对左右两侧的数列分别按照1，2处理，直至 ***只剩下一个数***迭代停止

def qick_sort(list_in):
if len(list_in) < 2:
return list_in
#如果list中只有1个值或者为空就返回
i = 0
j = len(list_in) - 1
mid = list_in[(i + j) // 2]
#以中间的值作为分割值
left = []
right = []
list_in.remove(mid)
#先把中间的值去掉
for ele in list_in: #遍历list
if ele < mid:
#如果值小于中间的值，那么放入左列表
left.append(ele)
else:
right.append(ele) #如果大于放到右列表
#迭代左右两个子列表，并且合并在一起组成新的list
return qick_sort(left) + [mid] + qick_sort(right)

一行代码使用lambda函数的形式

array = [0,1,2,1]
#这里是使用的array[0]作为分割值
quick_sort = lambda array: array if len(array) < 2 else quick_sort([item for item in array[1:] if item <= array[0] ]) + [array[0]] + quick_sort([item for item in array[1:] if item > array[0]])
print(quick_sort(array))

这样的快排方法，最差情况下的时间复杂度O($n^2$)，不是最差的情况下是O($nlogn$)。所以该方法是可以适当优化的。优化方法：

1. 每次随机选取元素，这样出现最差的情况的可能就会尽可能小
2. 因为可能会有大量重复的元素，这样导致我们的算法每次在left和right里面都将重复的元素单个处理，那我们定义left，mid，right三个列表，三路快排，这样减少了重复元素的运算

def qick_sort(list_in):
if len(list_in) < 2:
return list_in
i = 0
j = len(list_in) - 1
seg = list_in[(i + j) // 2]
left = []
right = []
mid = [] #加入mid数组为了存储相等的数值
list_in.remove(seg)
for ele in list_in:
if ele < seg:
left.append(ele)
elif ele == seg:
mid.append(ele)
else:
right.append(ele)
return qick_sort(left) + mid+[seg] + qick_sort(right)

一行算法

array = [0,1,2,1]
quick_sort = lambda array: array if len(array) < 2 else quick_sort([item for item in array[1:] if item < array[0] ]) + [item for item in array if item == array[0]] + quick_sort([item for item in array[1:] if item > array[0]])
print(quick_sort(array))

3. 插入排序

插入排序思想：

1. 第二个数开始与前一个比较，如果比前一个小，那么前一个位置后移一位，第二个数插入到第一个的位置
2. 以此类推，第三个数与前面一个比较，前面数小，那么前面的数后移一位
3. 直到最后一个数比较完

def InsertSort(lst):
for i in range(1,len(lst)):
target = lst[i]
#设置target
j = i
while j > 0 and lst[j-1] > target: #与target进行比较
lst[j] = lst[j-1] #如果比target小，那么后移一位，挪出位置
j = j-1
lst[j] = target
#插入相应的值
print(lst)

每轮操作n次，一共n轮，所以最后的时间复杂度是O($n^2$)

4. 希尔排序

希尔排序的思路是：

上面的插入排序相当于步长为1，一个一个比较，但是希尔排序相当于增加了步长，步长可以自己定义

1. 定义步长gap
2. 比较第i个数字，i in range(gap,n) 和第 i-gap 个数字的大小，如果前者大，那么更换两者之间的位置，直到 i-gap<0， 这时候i+1（如果这里有疑问的话，可以想i=10，gap=2，那么应该依次递归，第10位与第10-2位比，第10-2位与第10-2-2位比，以此类推。这不就像上面的插入排序的思路吗？）
3. 缩小gap，重复2，直到gap==1（这时候相当于插入排序，但是因为前面的做法使得这个数组已经基本有序，因此需要的更换的次数远远小于剑的插入排序）

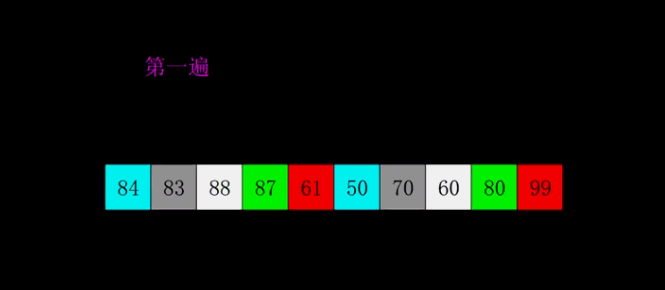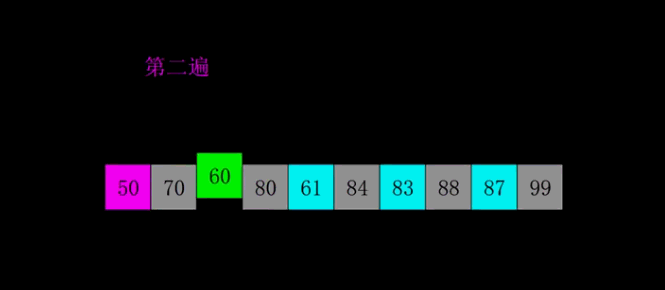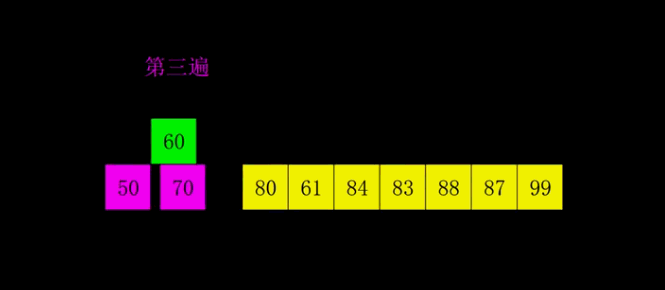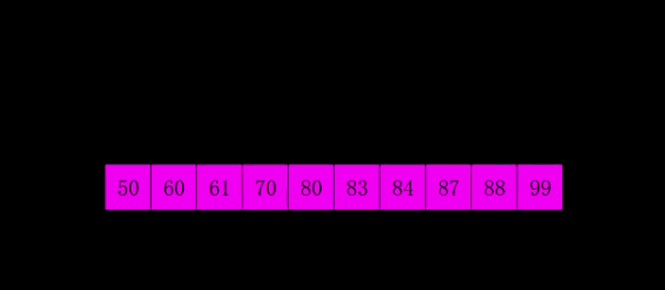
上面的如果看不懂，可以看这一张图：

def ShellSort(lst):
if len(lst) < 2:
return lst
n = len(lst)
gap = n//2
#定义初始间隔
while gap >= 1: #如果间隔小于1跳出循环
for i in range(gap, n):
j = i
while j - gap >= 0 and lst[j - gap] > lst[j]: #相当于比较步长为gap的两个数的大小，如果前面的大，那就互换位置
lst[j - gap], lst[j] = lst[j], lst[j - gap] #互换位置
j = j - gap
gap = gap//2
#减小gap，直至减少到相当于是插入排序的步长，gap=1
print(lst)

希尔排序的时间复杂度降低到了O($nlogn$)

5. 简单选择排序

简单排序的思想：

最简单的叙述就是循环i次，每次找第i到第len(lst)最小的一个数放到第i个位置。下面尽可能用最通俗的语言介绍：

1. 遍历整个数组，找到最小的数并记下其索引 j，然后将 j 位置上的数与第一个位置上的数交换，也就是最小的放在了前面。
2. 遍历第2个数到最后一个数，找到最小的数并且记下其索引 j， 然后将 j 位置上的数与第二个位置上的数交换，也就是整个数组上的第2小的数放到了第二个位置上。
3. 以此类推

def SelectionSort(lst):
n = len(lst)
if n < 2:
return lst
for i in range(n):
min_idx = i
for j in range(i,n):
if lst[j] < lst[min_idx]:
min_idx = j
lst[i], lst[min_idx] = lst[min_idx],lst[i]
print(lst)

表现的最稳定的排序方法，无论是什么样的数据最后的时间复杂度都是O($n^2$)。适用于数据规模小的情况。

6. 堆排序

堆排序主要是利用堆这样一种性质进行排序，如果想了解什么是堆，详细理解堆排序，请看我这一篇文章详解堆排序 python。
堆是一种近似完全二叉树，同时满足堆积的性质。即，父节点的键值和索引总是大于（或小于）子节点，称为大顶堆（小顶堆）。

1. 利用list构建大顶堆
2. 将大顶堆的根节点与最后一个节点互换位置
3. 利用除最后一个节点之外的节点，重新构造一个大顶堆
4. 将新的大顶堆的根节点与（大顶堆）最后一个节点（即整个数组倒数第二个节点，因为倒数第一个没有参加构建大顶堆的过程）互换位置
5. 以此类推，重复3，4。直至排完整个序列

def MaxHeapify(heap,heapsize,root):
left = 2*root+1
right = left+1
lager = root
if left < heapsize and heap[lager] < heap[left]:
lager = left
if right < heapsize and heap[lager] < heap[right]:
lager = right
if heap[root] != heap[lager]:
heap[root], heap[lager] = heap[lager], heap[root]
MaxHeapify(heap,heapsize,lager)
def BuildMaxHeapify(lst):
n = len(lst)
if n < 2:
return lst
for i in range(n//2, -1,-1):
MaxHeapify(lst,n,i)
def HeapifySort(lst):
BuildMaxHeapify(lst)
for i in range(len(lst)-1,-1,-1):
lst[0],lst[i] = lst[i],lst[0]
MaxHeapify(lst,i,0)
print(lst)

7. 二路归并排序

归并排序的思想是：

主要利用的是合并两个有序列表的思想，如果不知道怎样合并两个有序列表，那么可以看这里。合并两个有序列表，我们只需要设置两个指针，一个空的存储列表，一个指向第一个列表，另一个指向第二个列表，比较两指针指向的值的大小，将较小的值放入到空列表内，同时该指针向前移一位，再进行比较，以此类推。直至其中一个指针遍历完整个列表，把另一个列表内剩下的数全部存放到先前设置的存储列表中。所以归并排序的步骤如下

1. 进来的列表是一个无序列表，那么首先我们把它分为两个列表
2. 这两个列表也是无序的，不能利用上面的有序列表合并的思想，因此递归，将这两个列表分别再分。直到分为只剩下一个数的列表，那么这时候两个列表的合并就可以用到上述的有序列表合并。

#合并两个有序列表
def merge(a,b):
c = []
i = j = 0
while i < len(a) and j < len(b): #比较两个指针所指的位置的值的大小
if a[i] <= b[j]:
c.append(a[i])
i += 1
else:
c.append(b[j])
j += 1
if i == len(a):
c += b[j:]
else:
c += a[i:]
return c
#归并排序
def mergesort(lst):
n = len(lst)
if n < 2:
return lst
mid = n//2
a = mergesort(lst[:mid])
b = mergesort(lst[mid:])
c = merge(a,b)
return c

归并排序的时间复杂度是O(nlogn)，但是需要额外的存储空间。

8. 线性时间非比较类排序方法

8.1 计数排序

计数排序的基本思想是：

计数排序顾名思义，就是把列表中的每个数先从小到大统计一下个数，然后排序。步骤如下：

1. 先计算出list中最大的数和最小的数
2. 设置一个全为0的长度为max-min+1的list1
3. 遍历list，统计list中的每个元素item的个数并且填到list1中的item-min的位置上（为什么是item-min呢？因为最小值不一定为0，那么最小的数应该被统计在list1的第0位上，所以应该是min-min位置上）

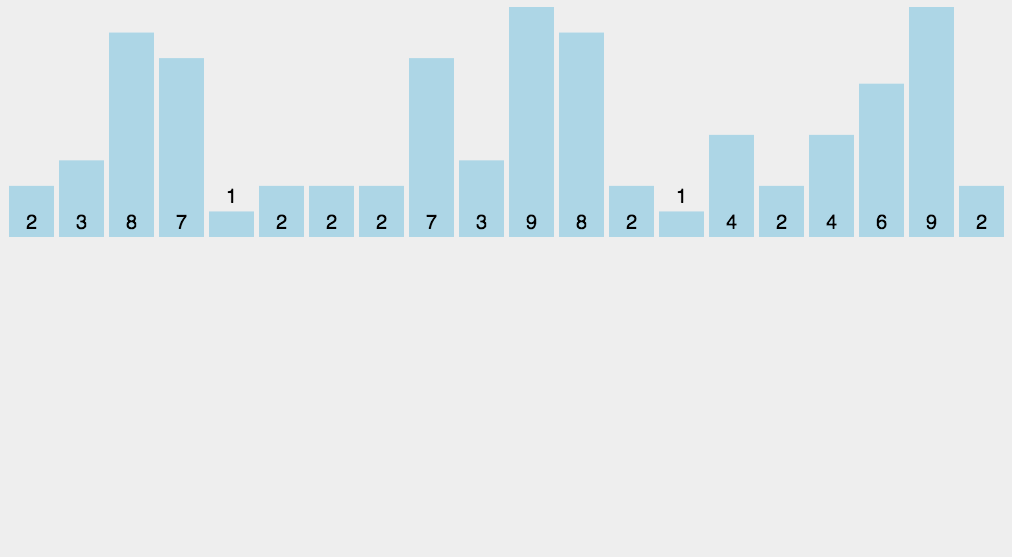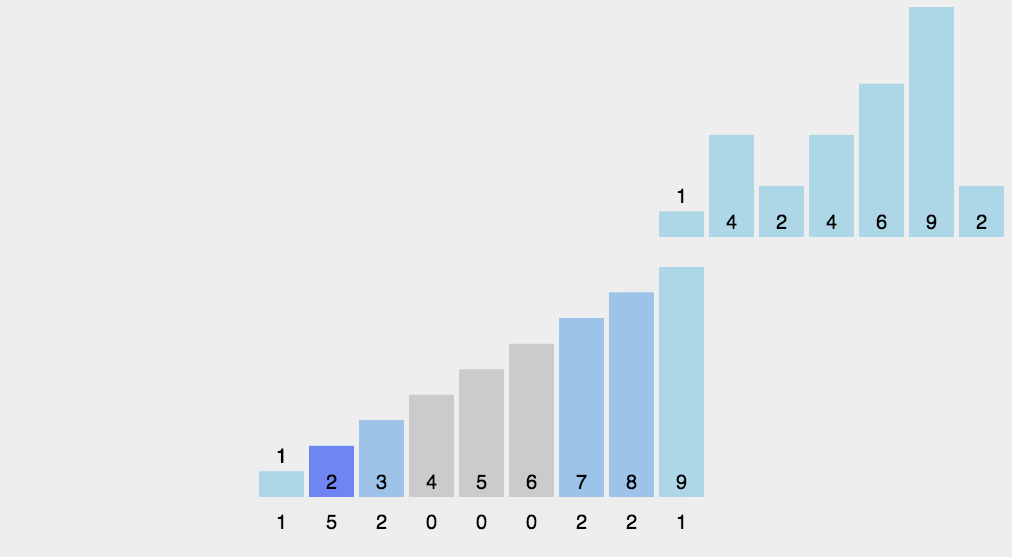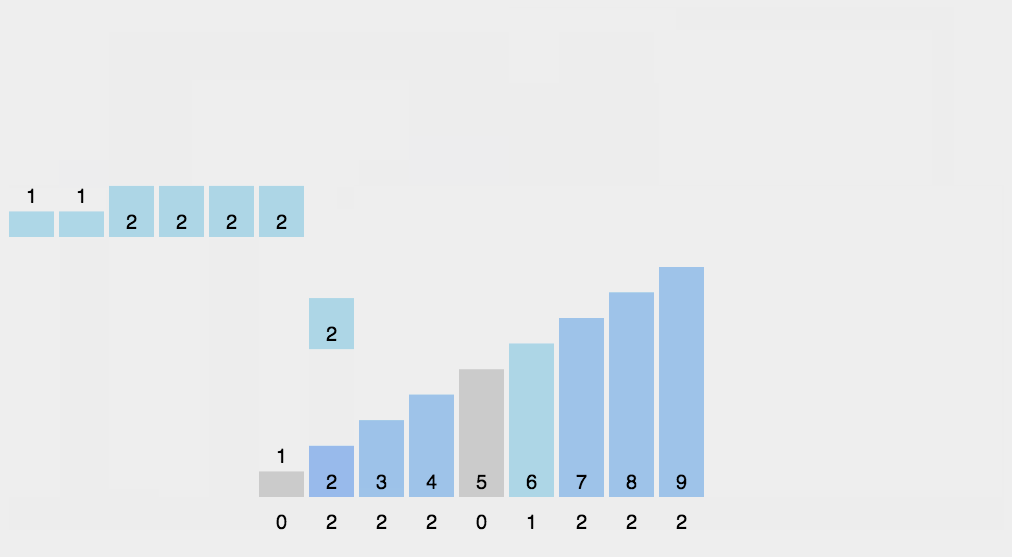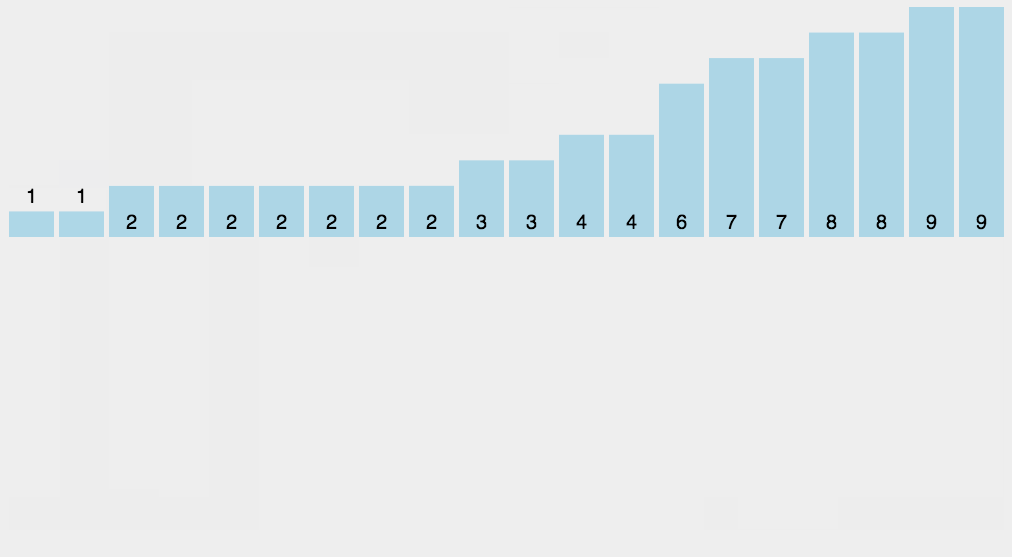
def CountSort(lst):
min_num = min(lst)
max_num = max(lst)
count = [0]*(max_num-min_num+1)
for item in lst:
count[item-min_num] += 1
res = []
for i in range(len(count)):
for j in range(0,count[i]):
res.append(i+min_num)
return res

从上面可以看出，计数排序只需要遍历一次列表list，但是需要遍历count列表，所以时间复杂度是O(n+k)，k表示有k个数，但是需要利用到额外的空间O(n)。

8.2 桶排序

桶排序的基本思想是：

与上述的计数排序类似，上面的计数排序相当于有n个桶，每个桶内最多装一个数。但是桶排序是每个桶内装一个范围内的数，一个桶内的数可以使用其他的一些排序方法，比如快排之类的。比如对于[4,4,3,1]，那么计数排序装的就是每个数的数量，桶排序的桶内装的是[4,4],[3],[1]。最后再将每个桶内排好的数合并在一起。

1. 设置一个数组当作空桶
2. 遍历数组把数字放到相应范围的桶内
3. 对桶内的数字进行排序（可以是快排等）
4. 把排序好的桶内数字拼接起来

def BucketSort(lst):
max_num = max(lst)
min_num = min(lst)
bucket_range = (max_num - min_num)/len(lst)
#设置桶中数字值的范围
bucket_list = [[] for _ in range(len(lst))]
# 设置一组空桶，有些可能完全不用装任何东西
for i in lst:
bucket_list[int((i-min_num)//bucket_range)].append(i)
#把相应的数字放到相应的桶内
res = []
for bucket in bucket_list:
for items in sorted(bucket): #对桶内的数字进行排序，这里使用了sorted的方法
res.append(items) #把排序好的数字按顺序放到数组中
print(res)

假设n个数据，划分为k个桶，桶内采用快速排序，时间复杂度为O(n)+O(k * n/klog(n/k))=O(n)+O(n(log(n)-log(k))),

显然，k越大，时间复杂度越接近O(n)，当然空间复杂度O(n+k)会越大，这是空间与时间的平衡。

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

8.3 基数排序

基数排序利用了桶排序的方法，总的思想是：

按照位数排序，先按照个位数排序，然后再按照十位数排序，依次排到最高位。为什么这样呢？可以看下面的动图

1. 取得数组中的最高位
2. 从最低位起，按照该位的数字的大小进行排序，形成新的数组
3. 对新的数组从高一位再次排序
4. 直到排到最高位

def RadixSort(lst):
if len(lst) < 2:
return lst
n = len(str(max(lst))) #选取最高位
for i in range(n):
bucket_list = [[] for _ in range(10)]
#建立10个桶，因为对于每位数来说都有10个数
for j in lst:
bucket_list[(j//(10**i))%10].append(j)
#按照该位的数的大小放入到相应的桶中
lst = [k for m in range(10) for k in bucket_list[m]]
print(lst)

面试常见问题

看到了就总结 ???? ???? ????

总结

参考：
https://zhuanlan.zhihu.com/p/60731708
十大经典排序算法（动图演示）
Python希尔排序算法
归并排序详解(Python | Java实现)
python实现·十大排序算法之桶排序(Bucket Sort)
利用Python实现堆排序

最后

以上就是可靠黄蜂为你收集整理的基础排序算法整理-超级简单易懂 python简介算法介绍面试常见问题总结的全部内容，希望文章能够帮你解决基础排序算法整理-超级简单易懂 python简介算法介绍面试常见问题总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。