「PyTorch深度学习入门」5. 学习的机制（上）

来源 | Deep Learning with PyTorch

作者 |  Stevens, et al.

译者 | 杜小瑞

校对 | gongyouliu

编辑 | auroral-L

全文共5215字，预计阅读时间35分钟。

本章内容包括：

√ 了解算法如何从数据中学习

√ 用微分法和梯度下降法将学习重构为参数估计

√ 剖析一个简单的学习算法

√ PyTorch如何支持autograd学习

第五章  学习的机制（上）

1.  一个跨越时间长河的建模案例

2.  学习只是参数估计

    2.1  热点问题

    2.2  收集一些数据

    2.3  数据可视化

    2.4  选择线性模型作为第一次尝试

3.  我们想要的是更小的误差

    3.1  从问题回到 Pytorch

随着机器学习在过去十年的蓬勃发展，从经验中学习的机器概念已经成为技术界和新闻界的主流主题。现在，机器究竟是如何学习的？这个过程的机制是什么？换句话说，它背后的算法是什么？从观察者的角度出发，这是一种输入数据与期望输出配对的学习算法。一旦开始学习，当输入的数据被算法训练的与新数据足够相似时，它将能够产生正确的输出。在深度学习中，即使输入数据和期望输出相差甚远，比如当他们来自不同的领域，就像我们在第二章看到的一个图像和一个描述它的句子，这个过程也能正常工作。

1. 一个跨越时间长河的建模案例

建立模型，让我们能够解释输入/输出关系的方法至少可以追溯到几个世纪前。当德国数学天文学家约翰内斯·开普勒（Johannes Kepler，1571-1630）在17世纪早期发现行星运动的三条定律时，他是根据他的导师第谷·布拉赫（Tycho Brahe）在肉眼观察时收集的数据（是的，用肉眼看并写在一张纸上）来推导的。由于没有牛顿万有引力定律（实际上，牛顿利用开普勒的工作来解决问题），开普勒推断出了最简单的几何模型来拟合数据。顺便说一句，他花了六年时间盯着那些对他来说毫无意义的数据，加上增量实现，最终发现了规律。我们可以在图5.1中看到这个过程。

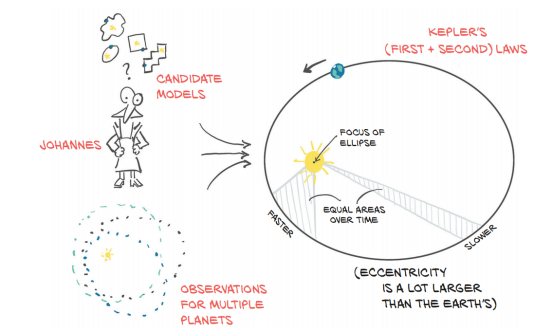
图 5.1 约翰内斯·开普勒考虑了多个候选模型，这些模型可能适合手头的数据，确定在一个椭圆上

开普勒的第一定律是：“每个行星的轨道都是一个椭圆，太阳位于两个焦点之一。”他不知道是什么原因导致轨道椭圆，但他给出了对行星（或一个大行星的卫星，如木星）的观测，他可以估计椭圆的形状（偏心率）和大小（半焦距）。根据数据计算出的这两个参数，他可以判断出这颗行星在天空中运行时的位置。一旦他发现了第二定律——“一条连接行星和太阳的线在相等的时间间隔内扫出相等的面积”——他还可以根据时间上的观察，判断行星何时会在空间的某个特定点。

那么，开普勒是如何在没有电脑、计算器、甚至微积分的情况下估算椭圆的偏心率和半焦距的呢？在开普勒的时代，这些都还没有发明呢。但是我们可以从开普勒自己的回忆，在他的书《新天文学》中，或者从J.V.Field在他的系列文章《证据的起源》中提到(http://mng.bz/9007)东西看出来:

从本质上说，开普勒必须尝试不同的形状，用一定数量的观测值来找到曲线，然后用曲线来找到更多的位置，当他有观测值的时候，再检查这些计算出的位置是否与观测到的一致。

--J.V.Field

让我们总结一下。六年来开普勒做了什么：

1. 从他的朋友布拉赫那里得到了很多好数据（费尽周折）

2. 他试着想象这一切，因为他觉得有什么可疑的事情发生了

3. 选择最简单的模型，有机会拟合数据（椭圆）

4. 分割数据，这样他就可以处理其中的一部分，并保留一个独立的数据集进行验证

5. 从椭圆的一个试探性的偏心率和大小开始，然后迭代直到模型符合观测值

6. 在独立观察的基础上验证了他的模型

7. 难以置信地回头看

这里有一本从1609年开始的数据科学手册，科学的历史就是建立在这七个步骤上的。几个世纪以来，我们已经认识到，背离这些原则会导致灾难。

这正是我们将着手做的，以便从数据中学到一些东西。事实上，在这本书中，说我们将拟合数据和说我们将使算法从数据中学习实际上没有区别。这个过程总是涉及到一个具有许多未知参数的函数，这些参数的值是从数据中估计出来的：简而言之，就是一个模型。

我们可以说，从数据中学习假定基础模型不是为了解决特定问题而设计的（开普勒工作中的椭圆就是这样），而是能够逼近更广泛的函数族。一个神经网络本来可以很好地预测第谷·布拉赫的轨迹，而不需要开普勒的灵感来尝试将数据拟合成椭圆。然而，艾萨克·牛顿爵士要从一个通用模型中推导出他的万有引力定律要困难得多。

在这本书中，我们感兴趣的模型不是为解决一个特定的狭义任务而设计的，而是可以通过输入和输出对自动调整为专门处理许多类似任务中的任何一个的，换句话说，就是在与手头的特定任务相关的数据上训练的通用模型。特别是，PyTorch的设计使其易于创建模型，其中拟合误差相对于参数的导数可以解析地表示。如果对最后一句话不太理解，不用担心，下一步，我们有一个完整的部分，希望使你能够理解。

本章介绍如何自动化通用函数拟合。毕竟，这就是我们所做的，深度学习深度神经网络是我们所谈论的通用函数，PyTorch使这个过程尽可能简单和透明。为了确保我们正确理解关键概念，我们将从一个比深度神经网络简单得多的模型开始。这将使我们能够从本章的第一原理中理解学习算法的机制，因此我们可以在第6章中转向更复杂的模型。

2. 学习只是参数估计

在本节中，我们将学习如何获取数据、选择模型并估计模型的参数，以便对新数据进行良好的预测。为此，我们将抛开行星运动的复杂性，把注意力转移到物理学中第二难的问题上：校准仪器。

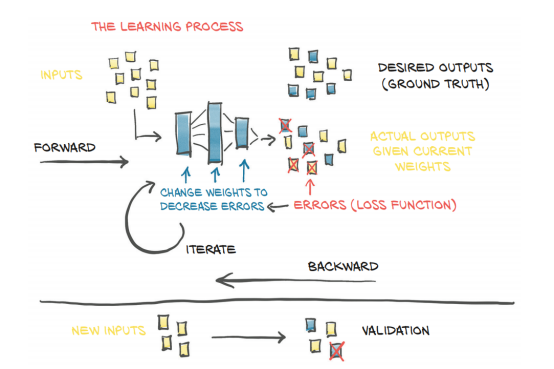
图 5.2 我们学习过程的思维模型

图5.2显示了我们将在本章末尾实现的内容的高级概述。给定输入数据和相应的期望输出（真实值）以及权重的初始值，将输入数据输入模型（前向传递），并通过将结果输出与真实值进行比较来评估误差度量。为了优化模型参数及其权重，使用复合函数导数的链式规则（向后传递）计算权重单位变化后的误差变化（即相对于参数的误差梯度）。然后在导致误差减小的方向上更新权重值。重复该程序，直到根据未知数据评估的误差降到可接受的水平以下。如果我们刚才说的话听上去晦涩难懂的话，我们还有整整一章要澄清。当我们完成的时候，所有的部分都将就位，这一段将非常有意义。

我们现在要处理一个有噪声数据集的问题，建立一个模型，并为它实现一个学习算法。当我们开始的时候，我们会手动来做所有的事情，但是到本章结束的时候，我们会让PyTorch为我们承担所有的工作。即使我们这里提供的有意思的示例非常简单，而且我们的模型实际上也不是一个神经网络，但当我们完成这一章时，我们将涵盖许多训练深层神经网络的基本概念。

2.1 热点问题

我们刚从一个偏僻的地方回来，带回来一个装在墙上的模拟温度计。它看起来很棒，非常适合我们的客厅。它唯一的缺点是没有显示单位。不用担心，我们有一个计划：我们将建立一个温度计读数和我们喜欢的温度单位的值对应的数据集，选择一个模型，调整其权重迭代，直到误差足够低，最后能够以我们理解的单位来解释测量的读数。

让我们试着遵循开普勒使用的相同过程。在此过程中，我们将使用一个他从未有过的工具：PyTorch！

2.2 收集一些数据

我们先把使用摄氏度衡量的温度数据和新温度计的测量值记录下来，然后把事情弄清楚。几周后，数据如下（code/p1ch5/1_parameter_estimation.ipynb）：

在这里，t_c值是以摄氏度为单位的温度数据，t_u值是未知单位的温度表示。我们可以预期来自设备本身和我们的近似读数这两个测量的数据中是存在噪声的。为了方便起见，我们已经把数据放入了张量中；现在我们就可以使用这些数据。

2.3 数据可视化

图5.3中我们的数据的快速绘图告诉我们它是有噪声的，但是我们认为这里一定有规律可循。

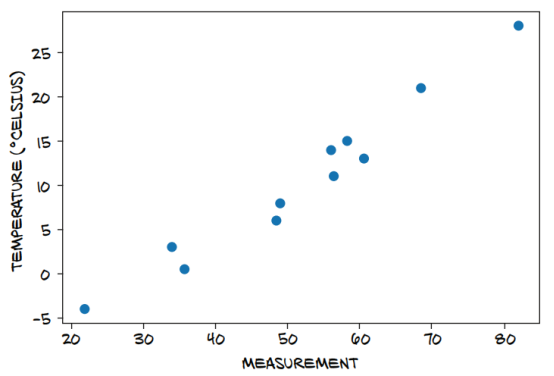
图 5.3 我们未知的数据可能遵循线性模型

注意 

我们知道线性模型是正确的，因为问题和数据都是捏造的，但大家不要在意这一点。这是一个很好的例子，可以帮助我们理解PyTorch在幕后的所作所为。

2.4 选择线性模型作为第一次尝试

在缺乏进一步知识的情况下，我们假设两组测量值之间转换的最简单模型，就像开普勒可能做的那样。这两者可能是线性相关的，也就是说，乘以一个因子，再加上一个常数，我们可以得到摄氏度的温度（直到我们忽略的误差）：

这是合理的假设吗？可能；我们来看看最终模型的效果如何。我们选择将权重和偏差命名为w和b，这是线性标度和加法常数的两个非常常见的术语。

好的，现在我们需要基于我们的数据估计我们模型中的参数w和b。这样做的目的是使我们通过模型运行未知温度t_u得到的温度接近我们实际测量的摄氏温度。如果这听起来像是通过一组测量来拟合一条线，那么，是的，因为这正是我们正在做的。我们将使用PyTorch来学习这个简单的例子，并认识到训练神经网络基本上需要将模型更改为稍微复杂一点的模型，并增加几个（或很多个）参数。

让我们再回顾一下：我们有一个模型，其中有一些未知参数，我们需要估计这些参数，以便预测输出和测量值之间的误差尽可能小。我们注意到我们仍然需要精确地定义误差的度量。我们称之为损失函数，如果误差很高，则损失函数应该很高，理想情况下应该尽可能低以获得完美匹配。因此，我们的优化过程应该以找到w和b为目标，以使损失函数最小。

3. 我们想要的是更小的误差

损失函数（或代价函数）是一个计算单个数值的函数，学习过程将试图最小化该数值。损失的计算通常涉及一些训练样本的期望输出与模型在输入这些样本时实际产生的输出之间的差值。在我们的例子中，这将是我们的模型输出的预测温度t_p和实际测量值之间的差异，也就是t_p–t_c。

我们需要确保损失函数在t_p大于或小于真实t_c时使损失都为正，因为目标是t_p与t_c匹配。我们有几个选择，最直接的是| t_p–t_c |和（t_p–t_c）^2.根据我们选择的数学表达式，我们可以强调或忽略某些错误。从概念上讲，损失函数是一种优先考虑从训练样本中修复哪些错误的方法，因此我们的参数更新会导致对高权重样本的输出进行调整，而不是对其他一些损失较小的样本的输出进行更改。

这两个例子损失函数在0处都有一个明显的最小值，并且随着预测值向任一方向远离真值而单调增长，因为增长的陡度也随着远离最小值而单调增长，所以这两个函数都被称为凸函数。由于我们的模型是线性的，因此作为w和b的函数的损失也是凸的，当损失是模型参数的凸函数时，通常很难处理，因为我们可以通过专门的算法非常有效地找到最小值。但是，我们将在本章中使用功能较弱但更普遍适用的方法。我们这样做是因为对于我们最终感兴趣的深层神经网络，损失不是输入的凸函数。

对于我们的两个损失函数| t_p–t_c |和（t_p–t_c）^2，如图5.4所示，我们注意到差的平方在最小值附近表现得更为良好：当t_p等于t_c时，误差平方损失对t_p的导数为零。另一方面，绝对值在我们想要收敛的地方有一个未定义的导数。这在实践中并不像看上去那样是一个问题，但我们将暂时坚持使用平方差。

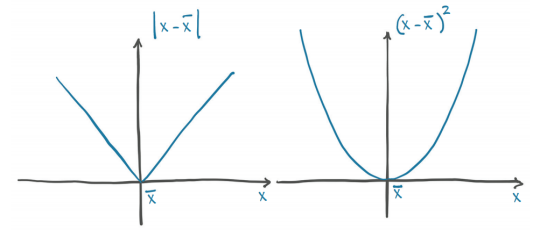
图 5.4 绝对差与平方差

值得注意的是，平方差比绝对差对错误结果的惩罚更大。通常，有更多的轻微错误的结果要比有几个严重错误的结果好，平方差有助于根据需要优先考虑这些结果。

3.1 从问题回到PyTorch

我们已经计算出了模型和损失函数，也已经计算出了图5.2中高级图的一部分。现在我们需要启动学习过程，并向它提供实际数据。另外，数学符号也足够了；让我们换成PyTorch来实现吧，毕竟，我们解决这个问题仅仅是为了好玩。

我们已经创建了数据张量，现在让我们将模型写成Python函数：

t_u、w和b分别是输入张量、权重参数和偏差参数。在我们的模型中，参数将是PyTorch标量（又称零维张量），乘积运算将使用广播产生返回的张量。不管怎样，是时候定义我们的损失了：

请注意，我们正在构建一个差分张量，将它们逐项求平方，最后对获得的张量按照各项求平均生成一个标量损失函数。这是一个均方损失。

我们现在可以初始化参数，调用模型，

并检查损失值：

我们实现了本节中的模型和损失。我们终于得到了这个例子的要点：我们如何估计w和b以使损失达到最小？我们将首先手工解决问题，然后学习如何使用PyTorch的超能力，以更通用、现成的方式解决同样的问题。

广播

我们在第三章提到了广播，我们承诺在需要的时候会更仔细地研究它。在我们的例子中，我们有两个标量（零维张量）w和b，我们用它们相乘，然后把它们加到长度为b的向量（一维张量）上。

通常，在PyTorch的早期版本中，我们也只能对相同形状的参数使用元素级的二元操作，如加法、减法、乘法和除法。每个张量中匹配位置的条目将用于计算结果张量中的相应条目。

广播，在NumPy和PyTorch中得到了广泛的使用，它放宽了大多数二元操作的这一假设。使用以下规则来匹配张量元素：

√ 对于从后面开始计算的每个索引维度，如果其中一个操作数在该维度中的大小为1，PyTorch将使用沿该维度的单个条目以及沿该维度的另一个张量中的每个条目。

√ 如果两个尺寸都大于1，则必须相同，并使用自然匹配。

√ 如果一个张量比另一个张量有更多的索引维度，那么另一个张量的整体将用于这些维度上的每个条目。

这听起来很复杂（如果我们不密切注意的话，它很容易出错，这就是为什么我们在第3.4节中命名了张量维度），但是通常，我们可以写下张量维度来查看发生了什么，或者通过使用空间维度来显示广播并描绘发生了什么，如下图所示。

当然，如果我们没有一些代码示例，那么这些就仅仅是理论了：

剩下的内容，请继续关注「数据与智能」~