数据挖掘实践(金融风控-贷款违约预测)(五):模型融合
目录
- 数据挖掘实践(金融风控-贷款违约预测)(五):模型融合
- 1.引言
- 2.模型融合的方式
- 2.1 Voting/Averaging
- 2.2 Boosting
- 2.3 Bagging
- 2.4 Stacking
- 2.5 Blending
- 2.6 Boosting与Bagging的比较
- 2.7 stackingblending详解
- 3.实战
- 3.1 平均
- 3.2 投票
- 3.3 blending
- 3.4 Stacking
- 4.总结
- 参考资料
1.引言
一般机器学习是通过挑选合适的单一模型算法,来得到尽可能高鲁棒性的数据模型,但从单一模型进行提升有一定的局限性,因此新的方法应运而生,即采用集成学习中模型融合的方法,将多个基分类器融合起来使用。
模型融合的思想是在单一模型的预测结果上,再使用模型融合方法来进一步提高模型预测的准确率。
目标
将之前建模调参的结果进行模型融合。(模型融合一般用于A榜比赛的尾声和B榜比赛的全程)
最终结果:(暂时排名98,尽力了,不会)
项目地址:https://github.com/datawhalechina/team-learning-data-mining/tree/master/FinancialRiskControl
比赛地址:https://tianchi.aliyun.com/competition/entrance/531830/introduction
2.模型融合的方式
模型融合是比赛后期上分的重要手段,特别是多人组队学习的比赛中,将不同队友的模型进行融合,可能会收获意想不到的效果哦,往往模型相差越大且模型表现都不错的前提下,模型融合后结果会有大幅提升,以下是模型融合的方式。
常见的集成学习&模型融合方法包括:简单的Voting/Averaging(分别对于分类和回归问题)、Stacking、Boosting和Bagging。
2.1 Voting/Averaging
在不改变模型的情况下,直接对各个不同的模型预测的结果,进行投票或者平均,这是一种简单却行之有效的融合方式。
比如对于分类问题,假设有三个相互独立的模型,每个正确率都是70%,采用少数服从多数的方式进行投票。那么最终的正确率将是:
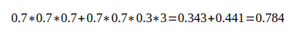
即结果经过简单的投票,使得正确率提升了8%。这是一个简单的概率学问题——如果进行投票的模型越多,那么显然其结果将会更好。但是其前提条件是模型之间相互独立,结果之间没有相关性。越相近的模型进行融合,融合效果也会越差。
比如对于一个正确输出全为1的测试,我们有三个很相近的的预测结果,分别为:

进行投票其结果为:
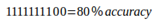
而假如我们的各个预测结果之间有很大差异:

其投票结果将为:
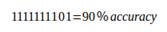
可见模型之间差异越大,融合所得的结果将会更好。这种特性不会受融合方式的影响。注意这里所指模型之间的差异,并不是指正确率的差异,而是指模型之间相关性的差异。
对于回归问题,对各种模型的预测结果进行平均,所得到的结果通过能够减少过拟合,并使得边界更加平滑,单个模型的边界可能很粗糙。这是很直观的性质,随便放张图②就不另外详细举例了。
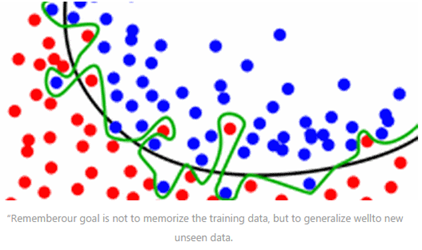
在上述融合方法的基础上,一个进行改良的方式是对各个投票者/平均者分配不同的权重以改变其对最终结果影响的大小。对于正确率低的模型给予更低的权重,而正确率更高的模型给予更高的权重。这也是可以直观理解的——想要推翻专家模型(高正确率模型)的唯一方式,就是臭皮匠模型(低正确率模型) 同时投出相同选项的反对票。具体的对于权重的赋值,可以用正确率排名的正则化等。
这种方法看似简单,但是却是下面各种“高级”方法的基础。
2.2 Boosting
Boosting是一种将各种弱分类器串联起来的集成学习方式,每一个分类器的训练都依赖于前一个分类器的结果,顺序运行的方式导致了运行速度慢。和所有融合方式一样,它不会考虑各个弱分类器模型本身结构为何,而是对训练数据(样本集)和连接方式进行操纵以获得更小的误差。但是为了将最终的强分类器的误差均衡,之前所选取的分类器一般都是相对比较弱的分类器,因为一旦某个分类器较强将使得后续结果受到影响太大。所以多用于集成学习而非模型融合(将多个已经有较好效果的模型融合成更好的模型)。
这里引用知乎专栏 《【机器学习】模型融合方法概述》③处引用的加州大学欧文分校Alex Ihler教授的两页PPT:
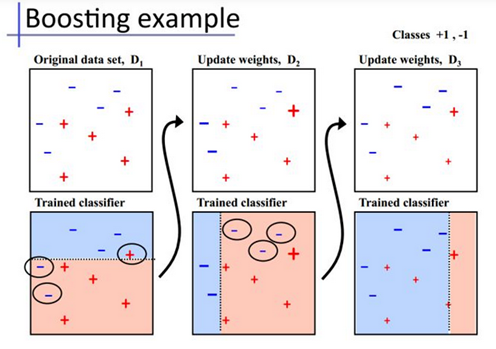
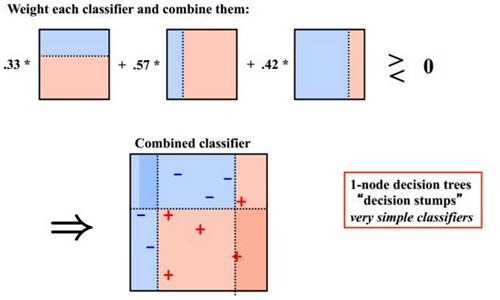 其基本工作机制如下:
其基本工作机制如下:
1、从初始样本集中训练出一个基学习器;
2、根据基学习器的表现对样本集分布进行调整,使得做错的样本能在之后的过程中受到更多的关注;
3、用调整后的样本集训练下一个基学习器;
4、重复上述步骤,直到满足一定条件。
注意,一般只有弱分类器都是同一种分类器(即同质集成)的时候,才将弱分类器称为基学习器,如果是异质集成,则称之为个体学习器。由于不是本文重点,所以此处不作区分。特此说明。
最终将这些弱分类器进行加权相加。
常见的Boosting方法有Adaboost、GBDT、XGBOOST等。 下面仅从思想层次上简单介绍各种方法,具体的算法推理公式推导以及可用的工具包等参考本文附录。
2.3 Bagging
Bagging是Bootstrap Aggregating的缩写。这种方法同样不对模型本身进行操作,而是作用于样本集上。采用的是随机有放回的选择训练数据然后构造分类器,最后进行组合。与Boosting方法中各分类器之间的相互依赖和串行运行不同,Bagging方法中基学习器之间不存在强依赖关系,且同时生成并行运行。
其基本思路为:
1、在样本集中进行K轮有放回的抽样,每次抽取n个样本,得到K个训练集;
2、分别用K个训练集训练得到K个模型。
3、对得到的K个模型预测结果用投票或平均的方式进行融合。
在这里,训练集的选取可能不会包含所有样本集,未被包含的数据成为包/袋外数据,可用来进行包外误差的泛化估计。每个模型的训练过程中,每次训练集可以取全部的特征进行训练,也可以随机选取部分特征训练,例如极有代表性的随机森林算法就是每次随机选取部分特征。
下面仅从思想层面介绍随机森林算法:
1、在样本集中进行K轮有放回的抽样,每次抽取n个样本,得到K个训练集,其中n一般远小于样本集总数;
2、选取训练集,在整体特征集M中选取部分特征集m构建决策树,其中m一般远小于M;
3、在构造每棵决策树的过程中,按照选取最小的基尼指数进行分裂节点的选取进行决策树的构建。决策树的其他结点都采取相同的分裂规则进行构建,直到该节点的所有训练样例都属于同一类或者达到树的最大深度;
4、重复上述步骤,得到随机森林;
5、多棵决策树同时进行预测,对结果进行投票或平均得到最终的分类结果。
多次随机选择的过程,使得随机森林不容易过拟合且有很好的抗干扰能力。
2.4 Stacking
“Here be dragons. With 7 heads. Standing on top of 30 other dragons. ”
接下来介绍在各种机器学习比赛中被誉为“七头龙神技”的Stacking方法。(但因其模型的庞大程度与效果的提升程度往往不成正比,所以一般很难应用于实际生产中。)
下面以一种易于理解但不会实际使用的两层的stacking方法为例,简要说明其结构和工作原理:(这种模型问题将在后续说明)
假设我们有三个基模型M1,M2,M3,用训练集对其进行训练后,分别用来预测训练集和测试集的结果,得到P1,T1,P2,T2,P3,T3
这种方法的问题在于,模型M1/2/3是我们用整个训练集训练出来的,我们又用这些模型来预测整个训练集的结果,毫无疑问过拟合将会非常严重。因此在实际应用中往往采用交叉验证的方法来解决过拟合问题。
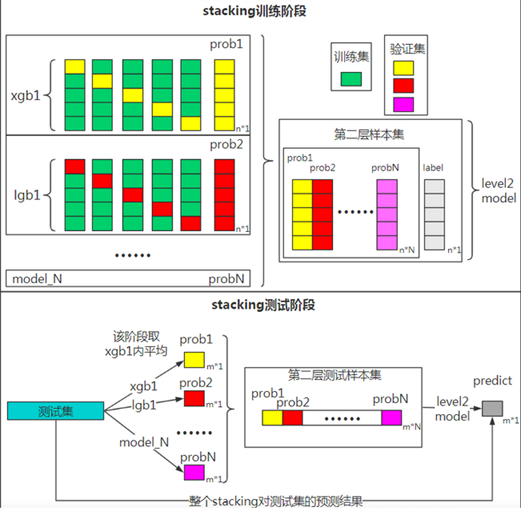
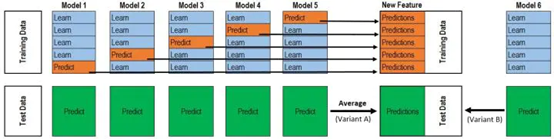
首先放几张图,我们着眼于Stacking方法的第一层,以5折交叉验证为例说明其工作原理:
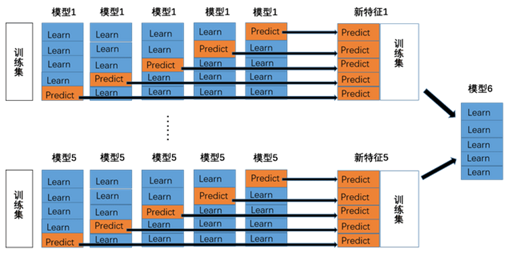
1、首先我们将训练集分为五份。
2、对于每一个基模型来说,我们用其中的四份来训练,然后对未用来的训练的一份训练集和测试集进行预测。然后改变所选的用来训练的训练集和用来验证的训练集,重复此步骤,直到获得完整的训练集的预测结果。
3、对五个模型,分别进行步骤2,我们将获得5个模型,以及五个模型分别通过交叉验证获得的训练集预测结果。即P1、P2、P3、P4、P5。
4、用五个模型分别对测试集进行预测,得到测试集的预测结果:T1、T2、T3、T4、T5。
5、将P15、T15作为下一层的训练集和测试集。在图中分别作为了模型6的训练集和测试集。
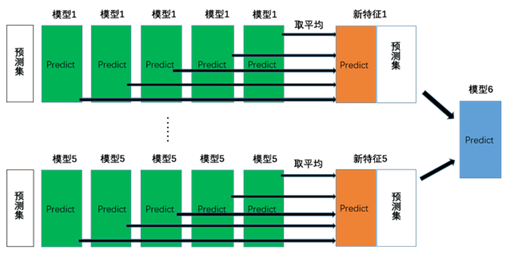
2.5 Blending
Blending是一种和Stacking很相像的模型融合方式,它与Stacking的区别在于训练集不是通过K-Fold的CV策略来获得预测值从而生成第二阶段模型的特征,而是建立一个Holdout集,例如10%的训练数据,第二阶段的stacker模型就基于第一阶段模型对这10%训练数据的预测值进行拟合。
说白了,就是把Stacking流程中的K-Fold CV 改成HoldOut CV。
以第一层为例,其5折HoldOut交叉验证将如下图所示:
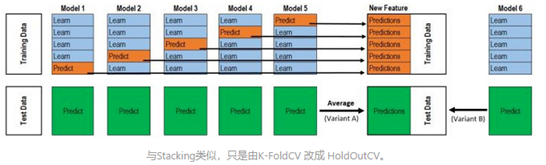
Stacking与Blending相比,Blending的优势在于:
1、Blending比较简单,而Stacking相对比较复杂;
2、能够防止信息泄露:generalizers和stackers使用不同的数据;
3、不需要和你的队友分享你的随机种子;
而缺点在于:
1、只用了整体数据的一部分;
2、最终模型可能对留出集(holdout set)过拟合;
3、Stacking多次交叉验证要更加稳健。
2.6 Boosting与Bagging的比较
优化方式上>
在机器学习中,我们训练一个模型通常是将定义的Loss最小化的过程。但是单单的最小化loss并不能保证模型在解决一般化的问题时能够最优,甚至不能保证模型可用。训练数据集的Loss与一般化数据集的Loss之间的差异被称为generalization error。
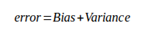
Variance过大会导致模型过拟合,而Bias过大会使得模型欠拟合。
Bagging方法主要通过降低Variance来降低error,Boosting方法主要通过降低Bias来降低error。
Bagging方法采用多个不完全相同的训练集训练多个模型,最后结果取平均。由于
所以最终结果的Bias与单个模型的Bias相近,一般不会显著降低Bias。
另一方面,对于Variance则有:
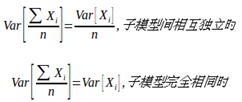
Bagging的多个子模型由不完全相同的数据集训练而成,所以子模型间有一定的相关性但又不完全独立,所以其结果在上述两式的中间状态。因此可以在一定程度上降低Variance从而使得总error减小。
Boosting方法从优化角度来说,是用forward-stagewise这种贪心法去最小化损失函数:
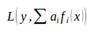
。所谓forward-stagewise,就是在迭代的第n步,求解新的子模型f(x)及步长a(或者称组合系数),来最小化
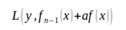
,这里
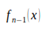
是前n步得到的子模型的和。因此Boosting在最小化损失函数,Bias自然逐步下降,而由于模型间强相关,不能显著降低Variance。
Bagging里面每个分类器是强分类器,因为他降低的是方差,方差过高需要降低是过拟合。
boosting里面每个分类器是弱分类器,因为他降低的是偏差,偏差过高是欠拟合。
样本选择上>
Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
样例权重>
Bagging:使用均匀取样,每个样例的权重相等
Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大
预测函数>
Bagging:所有预测函数的权重相等。
Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重
并行计算>
Bagging:各个预测函数可以并行生成
Boosting:理论上各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。计算角度来看,两种方法都可以并行。bagging,random forest并行化方法显而意见。boosting有强力工具stochastic gradient boosting
2.7 stackingblending详解
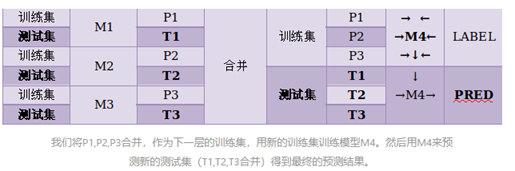
- stacking 将若干基学习器获得的预测结果,将预测结果作为新的训练集来训练一个学习器。如下图 假设有五个基学习器,将数据带入五基学习器中得到预测结果,再带入模型六中进行训练预测。但是由于直接由五个基学习器获得结果直接带入模型六中,容易导致过拟合。所以在使用五个及模型进行预测的时候,可以考虑使用K折验证,防止过拟合。
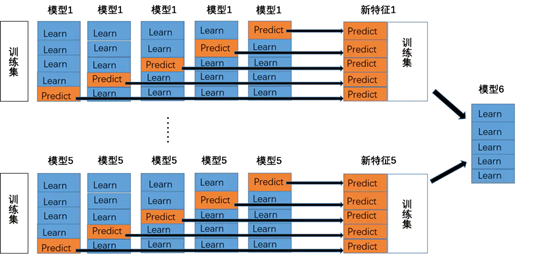
- blending 与stacking不同,blending是将预测的值作为新的特征和原特征合并,构成新的特征值,用于预测。为了防止过拟合,将数据分为两部分d1、d2,使用d1的数据作为训练集,d2数据作为测试集。预测得到的数据作为新特征使用d2的数据作为训练集结合新特征,预测测试集结果。
- Blending与stacking的不同
① stacking
stacking中由于两层使用的数据不同,所以可以避免信息泄露的问题。
在组队竞赛的过程中,不需要给队友分享自己的随机种子。
② Blending
由于blending对将数据划分为两个部分,在最后预测时有部分数据信息将被忽略。
同时在使用第二层数据时可能会因为第二层数据较少产生过拟合现象。
3.实战
3.1 平均
- 简单加权平均,结果直接融合 求多个预测结果的平均值。pre1-pren分别是n组模型预测出来的结果,将其进行加权融
pre = (pre1 + pre2 + pre3 +...+pren )/n
- 加权平均法 一般根据之前预测模型的准确率,进行加权融合,将准确性高的模型赋予更高的权重。
pre = 0.3pre1 + 0.3pre2 + 0.4pre3
3.2 投票
- 简单投票
from xgboost import XGBClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=4, min_child_weight=2, subsample=0.7,objective='binary:logistic')
vclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('xgb', clf3)])
vclf = vclf .fit(x_train,y_train)
print(vclf .predict(x_test))
- 加权投票
在VotingClassifier中加入参数 voting=‘soft’, weights=[2, 1, 1],weights用于调节基模型的权重
from xgboost import XGBClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=4, min_child_weight=2, subsample=0.7,objective='binary:logistic')
vclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('xgb', clf3)], voting='soft', weights=[2, 1, 1])
vclf = vclf .fit(x_train,y_train)
print(vclf .predict(x_test))
3.3 blending
# 以python自带的鸢尾花数据集为例
data_0 = iris.data
data = data_0[:100,:]
target_0 = iris.target
target = target_0[:100]
#模型融合中基学习器
clfs = [LogisticRegression(),
RandomForestClassifier(),
ExtraTreesClassifier(),
GradientBoostingClassifier()]
#切分一部分数据作为测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=914)
#切分训练数据集为d1,d2两部分
X_d1, X_d2, y_d1, y_d2 = train_test_split(X, y, test_size=0.5, random_state=914)
dataset_d1 = np.zeros((X_d2.shape[0], len(clfs)))
dataset_d2 = np.zeros((X_predict.shape[0], len(clfs)))
for j, clf in enumerate(clfs):
#依次训练各个单模型
clf.fit(X_d1, y_d1)
y_submission = clf.predict_proba(X_d2)[:, 1]
dataset_d1[:, j] = y_submission
#对于测试集,直接用这k个模型的预测值作为新的特征。
dataset_d2[:, j] = clf.predict_proba(X_predict)[:, 1]
print("val auc Score: %f" % roc_auc_score(y_predict, dataset_d2[:, j]))
#融合使用的模型
clf = GradientBoostingClassifier()
clf.fit(dataset_d1, y_d2)
y_submission = clf.predict_proba(dataset_d2)[:, 1]
print("Val auc Score of Blending: %f" % (roc_auc_score(y_predict, y_submission)))
3.4 Stacking
# Stacking
import warnings
import itertools
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
from sklearn.model_selection import cross_val_score, train_test_split
from mlxtend.plotting import plot_decision_regions
warnings.filterwarnings('ignore')
# 以python自带的鸢尾花数据集为例
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
label = ['KNN', 'Random Forest', 'Naive Bayes', 'Stacking Classifier']
clf_list = [clf1, clf2, clf3, sclf]
fig = plt.figure(figsize=(10, 8))
gs = gridspec.GridSpec(2, 2)
grid = itertools.product([0, 1], repeat=2)
clf_cv_mean = []
clf_cv_std = []
for clf, label, grd in zip(clf_list, label, grid):
scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
print("Accuracy: %.2f (+/- %.2f) [%s]" % (scores.mean(), scores.std(), label))
clf_cv_mean.append(scores.mean())
clf_cv_std.append(scores.std())
clf.fit(X, y)
ax = plt.subplot(gs[grd[0], grd[1]])
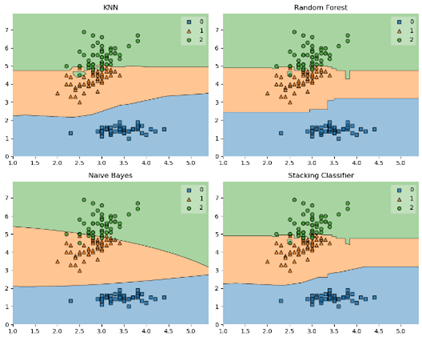
fig = plot_decision_regions(X=X, y=y, clf=clf)
plt.title(label)
plt.show()
结果:
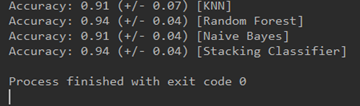
4.总结
简单平均和加权平均是常用的两种比赛中模型融合的方式。其优点是快速、简单。
stacking在众多比赛中大杀四方,但是跑过代码的小伙伴想必能感受到速度之慢,同时stacking多层提升幅度并不能抵消其带来的时间和内存消耗,所以实际环境中应用还是有一定的难度,同时在有答辩环节的比赛中,主办方也会一定程度上考虑模型的复杂程度,所以说并不是模型融合的层数越多越好的。
当然在比赛中将加权平均、stacking、blending等混用也是一种策略,可能会收获意想不到的效果哦!
参考资料
- 数据挖掘实践(金融风控)
- 零基础入门数据挖掘 - 贷款违约预测
- 模型融合方法总结
最后
以上就是闪闪电灯胆最近收集整理的关于数据挖掘实践(金融风控-贷款违约预测)(五):模型融合数据挖掘实践(金融风控-贷款违约预测)(五):模型融合的全部内容,更多相关数据挖掘实践(金融风控-贷款违约预测)(五)内容请搜索靠谱客的其他文章。

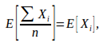








发表评论 取消回复