关于高次幂的取余问题（一稿）

   题目如下：

题目大概意思即是写出一段代码求出a^b%c的结果，看起来很简单，所以直接按照题干意思，写出代码如下：

 （这里有个注意事项，要把pow输出的double变为int类型赋值给d）

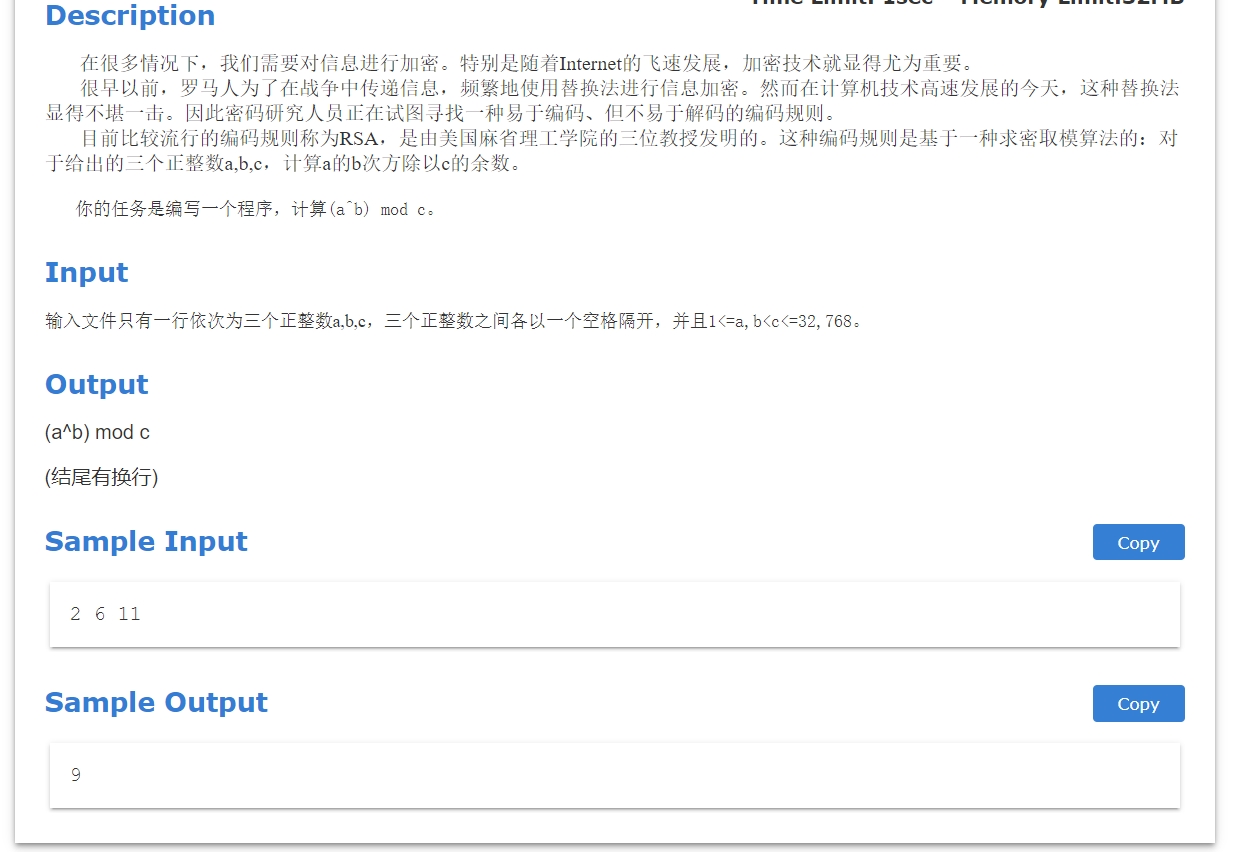
按照题目参考数据输出结果如下：

 结果是正确的。

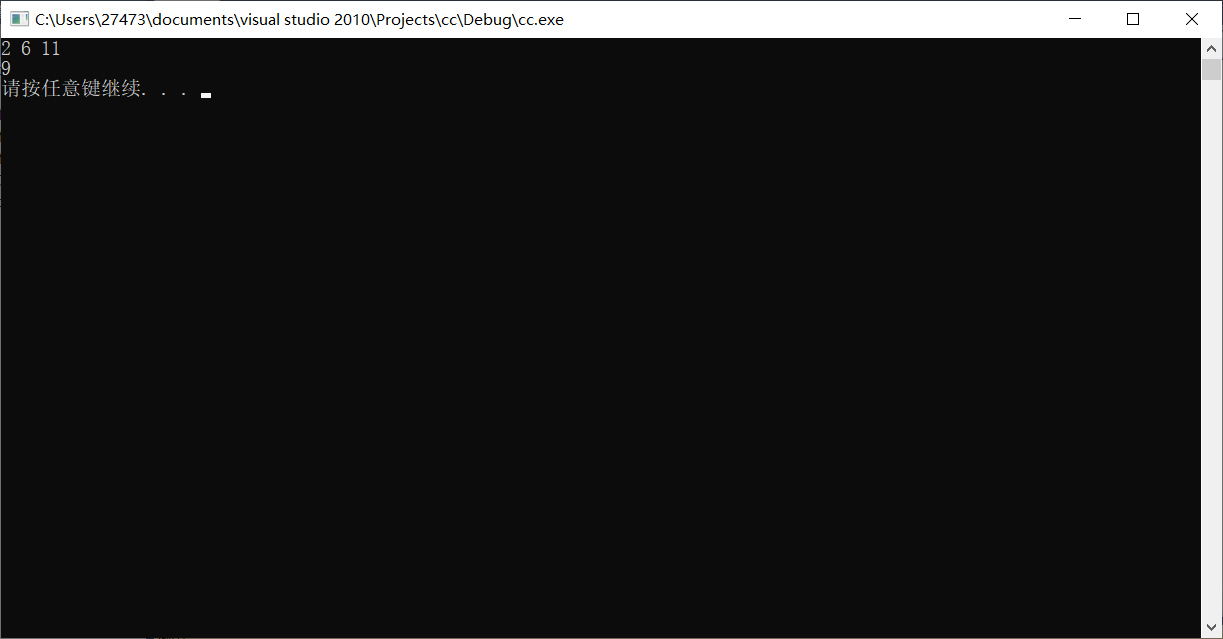
乍一看，好像已经完全满足题目的要求，我们要做的事情只是让计算机算出a^b的值再对c取余即可得出结果。但好奇的我对此产生了思考：万一a，b，c的值都很大呢？也正确吗？

 结果得出了这样的结果。很明显是不正确的。

仔细想想，a的b次方是一个正数，再对c取余肯定也是一个正数，为什么最后会输出一个负数结果呢？

考虑到int的取值范围是-2^31~（2^31-1），推断出应该是a^b的数值溢出了，导致结果出错。

所以这种暴力求解的方法不可取，必须要找到另一种方法来找出结果。

 既然是由于整个式子数值太大了导致结果出错。因此考虑运用模的知识来对（a^b）%c进行化简。

首先举出有关模的运算规则：

(a + b) % p = (a % p + b % p) % p （1）

(a – b) % p = (a % p – b % p) % p （2）

(a * b) % p = (a % p * b % p) % p （3）

(a^b) % p = ((a % p)^b) % p （4）

结合律：

((a+b) % p + c) % p = (a + (b+c) % p) % p （5）

((a*b) % p * c)% p = (a * (b*c) % p) % p （6）

交换律：

(a + b) % p = (b+a) % p （7）

(a * b) % p = (b * a) % p （8）

分配律：

((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p （9）

重要定理：

若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；（10）

若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；（11）

若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a – c) ≡ (b – d) (%p)，

(a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)； （12）

（此运算规则转载自CSDN博主「GKHack」的原创文章，原文链接：https://blog.csdn.net/GKHack/article/details/46607293）

运用模的运算规则，我们可以将（a^b）%c转变为(a%c*(a^(b-1))%c)%c,

a^(b-1))%c又可以进一步拆成a和a的b-2次方，进而运用递归的方法实现。这就保证了每次（）%c的时候，括号里面的两个相乘的数一定小于c，从而数值不会溢出。

附上代码：

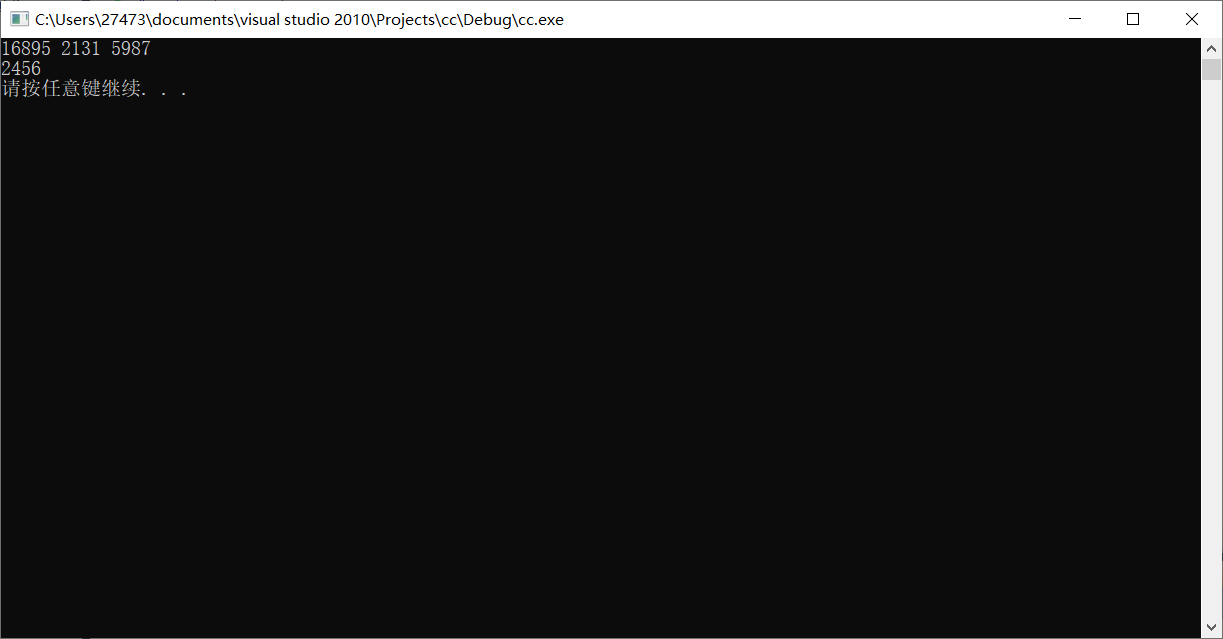
 结果1：

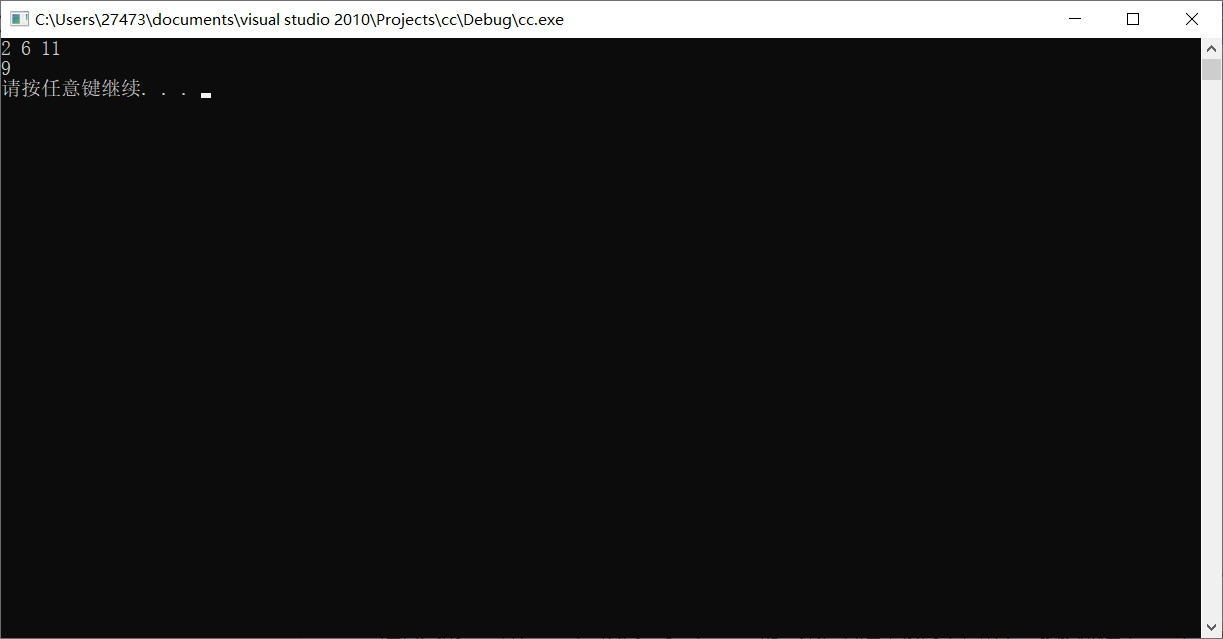
结果2（比较大）：

 反思：

1、计算机由于数值范围，往往不能够将一个表达式直接暴力求解，应该运用数学知识将其转化，同时也可以减少计算机的运算次数，加快运算。

2、另外，由于栈的内存分配问题，此代码有个缺陷就是递归次数不能太多，导致这里的次数b不能太高。至于如何解决这一问题，未完待续。

最后

以上就是帅气歌曲为你收集整理的关于高次幂的取余问题（一稿）的全部内容，希望文章能够帮你解决关于高次幂的取余问题（一稿）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。