力扣(LeetCode)1691. 堆叠长方体的最大高度(C++)

动态规划

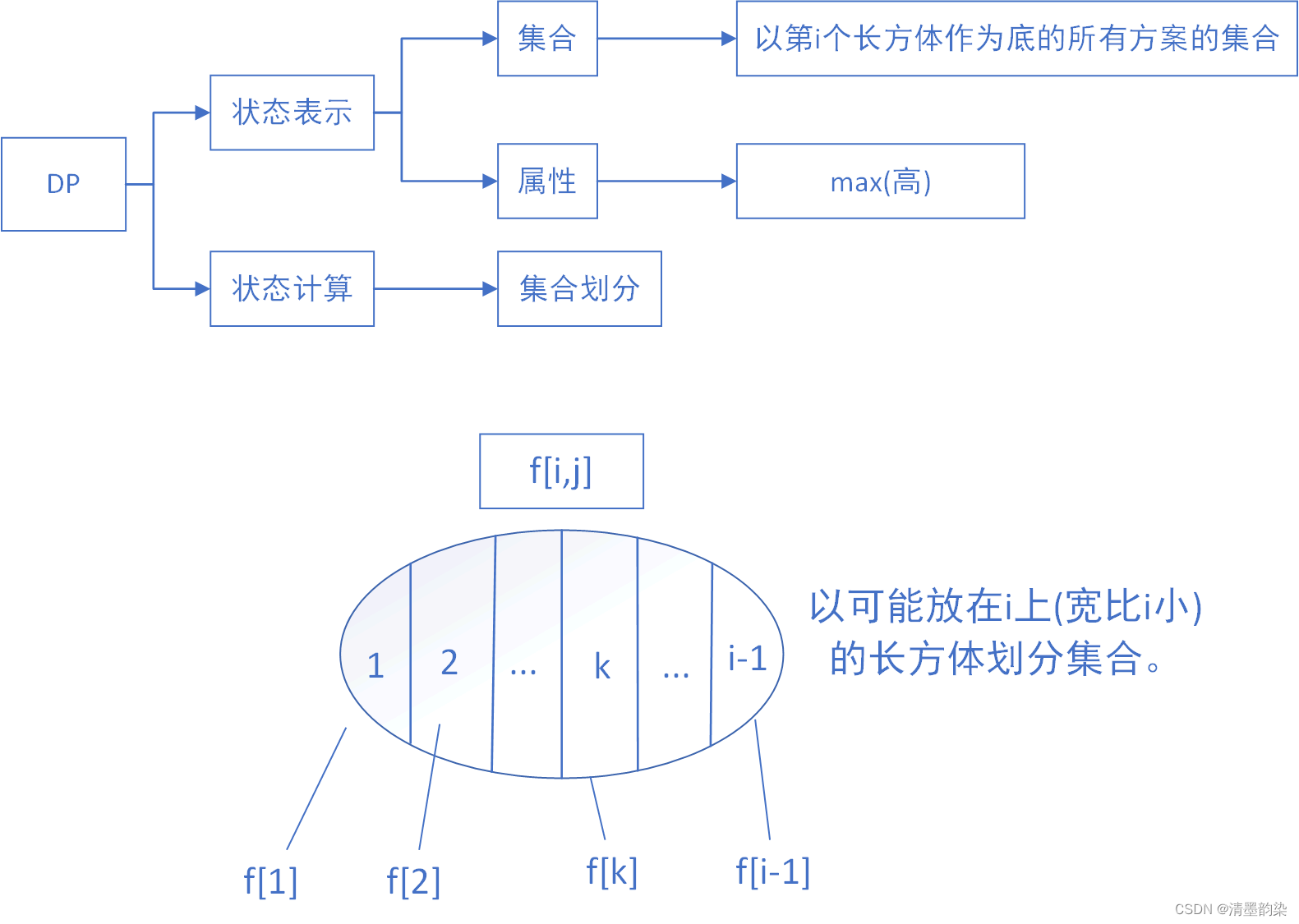
状态计算 :
$f[i]=\{\begin{array}{ll}cuboids[i][2]& \text{if }不存在k\\ max(f[k])+cuboids[i][2]& \text{if }k\in [1,i-1]\end{array}$

其中 $cuboids[i][2]$ 表示 $i$ 的高度。

设长方体 $A$ 的宽长高为 $w_1,l_1,h_1$ ，$B$ 的宽长高为 $w_2,l_2,h_2$
解题需要的性质 : 若 $w_1\le l_1\le h_1,w_2\le l_2\le h_2$ ，要 $A$ 可以堆叠在 $B$ 上，当且仅当 $w_1\le w_2$ 且 $l_1\le l_2$ 且 $h_1\le h_2$ 。
证明 :
①满足 $w_1\le w_2$ 且 $l_1\le l_2$ 且 $h_1\le h_2$ ，一定是符合题意的堆叠方案。
②要证明仅当，可以反证，假设当 $w_1>w_2$ 或 $l_1>l_2$ 或 $h_1>h_2$ ，$A$ 可以堆在 $B$ 上，

1. 当 $w_1>w_2$ ，
   有 $w_2<w_1\le l_1\le h_1$ ，
   仅当 $l_1\ge l_2$ 且 $h_1\ge h_2$ ，可以堆叠(包含在原命题)，($w_1>w_2$ 且 $l_1\ge l_2$ 且 $h_1\ge h_2$）
   其他情况不可堆叠。
2. 当 $l_1>l_2$ ，
   因为 $w_1\le l_1\le h_1$ , $w_2\le l_2\le h_2$ ，
   有$w_2\le l_2<l_1\le h_1$ ，
   则 $w_2$ 和 $l_2$ 只能与 $w_1$ 匹配，
   但 $w_1$ 只可匹配其中之一，
   不可以堆叠。
3. 当 $h_1>h_2$ ，
   有 $w_2\le l_2\le h_2<h_1$
   仅当 $w_1\ge w_2$ 且 $l_1\ge l_2$ ，可以堆叠(包含在原命题)
   其他情况不可堆叠。

综上，只有原命题成立，反证的结论才能成立，否则反证不成立。所以原命题成立。

class Solution {
public:
    int maxHeight(vector<vector<int>>& cuboids) {
        for(auto &c:cuboids) sort(c.begin(),c.end());
        sort(cuboids.begin(),cuboids.end());
        int n = cuboids.size();
        vector<int> f(n,0);
        int ans = 0;
        for(int i = 0;i<n;i++){
            f[i] = cuboids[i][2];
            for(int j = 0;j<i;j++)
                if(cuboids[i][1]>=cuboids[j][1]&&cuboids[i][2]>=cuboids[j][2])
                    f[i] = max(f[i],f[j]+cuboids[i][2]);
            ans = max(ans,f[i]);
        }
        return ans;
    }
};

1. 时间复杂度 : $O(n^2)$ ， $n$ 是长方体的数量，状态数量是 $n$ ，转移数量是 $n$ ，状态转移的时间复杂度 $O(n^2)$ 。
2. 空间复杂度 : $O(n)$ ，所有状态的空间复杂度 $O(n)$ 。

AC

致语

• 理解思路很重要
• 读者有问题请留言，清墨看到就会回复的。

最后

以上就是英勇牛排为你收集整理的力扣(LeetCode)1691. 堆叠长方体的最大高度(C++)的全部内容，希望文章能够帮你解决力扣(LeetCode)1691. 堆叠长方体的最大高度(C++)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。