HDU 5728 PowMod 欧拉函数公式推导+欧拉降幂

题意

令$k={\sum }_{i=1}^m\varphi (n\times i)mod10^9+7$,求$k^{k^{k^{k^{k^k......}}}}modp$.
$n,m,p\le 10^7$.

题解

首先计算$k$.根据下面的公式可以得到递归公式.

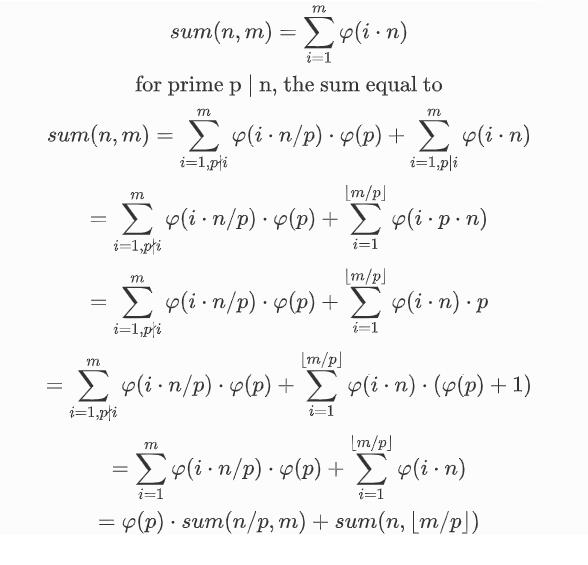
function<ll(ll,ll)> dfs=[&](ll n,ll m) {
  return !m?0:n==1?sum[m]:(phi[p[n]]*dfs(n/p[n],m)%mod+dfs(n,m/p[n]))%mod;
};

在这之前用线性筛欧拉函数辅助便可完成,其中$p_n$表示$n$最小的质因子,可以在线性筛中顺便完成.
接下来计算模$p$的余数.
由欧拉降幂公式可知,假设原式为$ans$,则$ans$无限大,因此在$gcd(k,p)\ne 1$时,一定满足$b>\varphi (p)$的条件,从而原式$=k^{ansmod\varphi (p)+\varphi (p)}modp$.
而对于$k,p$互质的情况,再加一遍$\varphi (p)$不影响答案,因此全部的情况都可以转化为一种可能.
那么我们采用递归的方法.
对于上面的$ansmod\varphi (p)$,再取出一个$k$,那么模数变成$\varphi (\varphi (p))$,反复嵌套欧拉函数之后不超过$log(p)$次模数就会变成$1$.
再嵌套一次快速幂,我们就解决了这题.

#include<bits/stdc++.h> //Ithea Myse Valgulious
using namespace std;
const int yuzu=1e7,mod=1e9+7;
typedef int fuko[yuzu|10];
fuko p,pr,phi,id,sum;
int main() {
  auto gphi=[&](int n) {
    int i,j;
    p[1]=phi[1]=1;
    for (i=2;i<=n;++i) {
      if (!p[i]) pr[++*pr]=p[i]=i,phi[i]=i-1;
      for (j=1;j<=*pr&&pr[j]*i<=n;++j) {
        p[pr[j]*i]=pr[j];
        if (i%pr[j]==0) {
          phi[pr[j]*i]=pr[j]*phi[i];
          break;
        }
        phi[pr[j]*i]=(pr[j]-1)*phi[i];
      }
    }
    for (i=1;i<=n;++i) sum[i]=(sum[i-1]+phi[i])%mod;
    return;
  };
  function<ll(ll,ll)> dfs=[&](ll n,ll m) {
    return !m?0:n==1?sum[m]:(phi[p[n]]*dfs(n/p[n],m)%mod+dfs(n,m/p[n]))%mod;
  };
  auto kasumi=[&](ll a,ll b,ll p) {
    ll zw=1;
    for (;b;b>>=1,a=a*a%p) if (b&1) zw=zw*a%p;
    return zw;
  };
  function<ll(ll,ll)> cal=[&](ll n,ll p) {
    return p==1?1:kasumi(n,cal(n,phi[p])+phi[p],p);
  };
  gphi(yuzu);
  ll n,m,p,k;
  for (;read(n),read(m),read(p);) {
    k=dfs(n,m);
    printf("%lldn",cal(k,p)%p);
  }
}

最后

以上就是妩媚西牛为你收集整理的HDU 5728 PowMod 欧拉函数公式推导+欧拉降幂的全部内容，希望文章能够帮你解决HDU 5728 PowMod 欧拉函数公式推导+欧拉降幂所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。