Codeforces 892E - Envy 【最小生成树】

46 阅读 0 评论 31 点赞

我是靠谱客的博主醉熏白开水，最近开发中收集的这篇文章主要介绍Codeforces 892E - Envy 【最小生成树】，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

E. Envy

time limit per test 2 seconds

memory limit per test 256 megabytes

For a connected undirected weighted graph G, MST (minimumspanning tree) is a subgraph of G that contains all of G's vertices, isa tree, and sum of its edges is minimum possible.

You are given agraph G. If you run a MST algorithm on graph it would give you only one MST and it causes other edges to become jealous. You are given some queries, each query contains a set ofedges of graph G, and you shoulddetermine whether there is a MST containing all these edges or not.

Input

The first line contains two integers n, m (2 ≤ n, m ≤ 5·10⁵, n - 1 ≤ m) — the number of vertices and edges in the graph and the number of queries.

The i-th of the next m lines contains three integers u_i, v_i, w_i (u_i ≠ v_i, 1 ≤ w_i ≤ 5·10⁵) — the endpoints and weight of the i-th edge. There can be more than one edges between two vertices. It's guaranteed that the given graph is connected.

The next line contains a single integer q (1 ≤ q ≤ 5·10⁵) — the number of queries.

q lines follow, the i-th of them contains the i-th query. Itstarts with an integer k_i (1 ≤ k_i ≤ n - 1) — the size of edges subset and continues with k_i distinct space-separated integers from 1 to m — theindices of the edges. It is guaranteed that the sum of k_i for 1 ≤ i ≤ q does not exceed 5·10⁵.

Output

For each query you should print "YES" (without quotes) if there's a MST containing these edges and "NO" (of course without quotes again) otherwise.

Example

Input

5 7
1 2 2
1 3 2
2 3 1
2 4 1
3 4 1
3 5 2
4 5 2
4
2 3 4
3 3 4 5
2 1 7
2 1 2

Output

YES
NO
YES
NO

Note

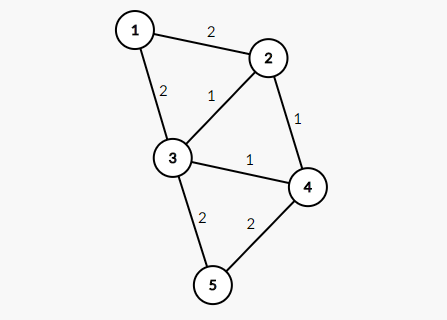
This is the graph of sample:

Weight of minimum spanning tree on this graph is 6.

MST with edges (1, 3, 4, 6), contains all of edges from the first query, so answer on the first queryis "YES".

Edges from the second query form a cycleof length 3, so there is nospanning tree including these three edges. Thus, answer is "NO".

【题意】

给你一系列边和其权值，保证利用这些边能够成最小生成树。再给出一系列询问，每个询问中有一些边，问这些边能否在一颗最小生成树中同时出现。

【思路】

首先我们明确一点，即对于一条权值为w的边来说，如果在所有权值小于w的边全部加入图后这条边的两个端点还没有联通的话，那么这条边能出现在最小生成树中。

而且对于每一组询问，权值相同的边会相互影响，而权值不相同的边的判断是相互独立的。

综上，我们得到一种做法：

先对给出边按权值排序记为A，再对询问中的边按权值(按询问)排序，记为B。

然后从小到大枚举B中的边权w，先把小于w的所有边加入到图G1中，然后把询问中边权为w的边一条条判断是否联通，若联通做标记，不连通的话在图G2中加入这条边。

值得注意的是，上一个操作第二步若边权等于w的边在多个询问中时，我们每次换到一个询问，应把G2还原为图G1，因为不同询问相同边权是不相互影响的。

具体细节见代码。

#include <cstdio>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define rush() int T;scanf("%d",&T);while(T--)
typedef long long ll;
const int maxn = 1000005;
const ll mod = 1e9+7;
const ll INF = 0x3f3f3f3f;
const double eps = 1e-9;
int n,m,k;
int pre[maxn];
int pa[maxn];
int mark[maxn];
int ans[maxn];
struct node
//储存边的信息
{
int u,v,w;
bool operator<(const node &a) const
{
return w<a.w;
}
}a[maxn];
struct query
//储存查询中边的信息
{
int id,u,v,w;
bool operator<(const query &a) const
{
if(w==a.w) return id<a.id;
return w<a.w;
}
}q[maxn];
int find(int x)
//原图并查集
{
return x==pre[x]?x:pre[x]=find(pre[x]);
}
int find2(int x,int tag)
{
if(mark[x]!=tag) pa[x]=pre[x],mark[x]=tag;
//不等于tag说明已经不在前一个询问里了，那么x点的前驱还原为在G1图中的前驱
return x==pa[x]?x:pa[x]=find2(pa[x],tag);
}
int main()
{
int x,y,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&w);
a[i]=(node){x,y,w};
}
scanf("%d",&k);
int tot=0;
for(int i=1;i<=k;i++)
{
scanf("%d",&x);
for(int j=1;j<=x;j++)
{
scanf("%d",&y);
q[++tot]=(query){i,a[y].u,a[y].v,a[y].w};
}
}
sort(a+1,a+1+m);
sort(q+1,q+1+tot);
for(int i=1;i<=n;i++) pre[i]=i,pa[i]=i;
int pos1=1,pos2=1;
int tag=0;
for(int i=1;i<=tot;i=pos2)
{
while(a[pos1].w<q[i].w&&pos1<=m)
//把权值小于w的边加入到图G1中
{
int A=find(a[pos1].u);
int B=find(a[pos1].v);
if(A!=B) pre[B]=A;
pos1++;
}
while(q[pos2].w==q[i].w&&pos2<=tot)
//枚举询问中权值等于w的边
{
if(pos2==i||q[pos2].id!=q[pos2-1].id) tag++;
//换了一个询问，需要还原
int A=find2(q[pos2].u,tag);
int B=find2(q[pos2].v,tag);
if(A==B) ans[q[pos2].id]=1;
else pa[B]=A;
pos2++;
}
}
for(int i=1;i<=k;i++)
{
if(ans[i]) puts("NO");
else puts("YES");
}
}