求无权图中指定两点的最短路径

60 阅读 0 评论 40 点赞

我是靠谱客的博主追寻毛衣，最近开发中收集的这篇文章主要介绍求无权图中指定两点的最短路径，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1、算法思想：
从给定的第一个点出发，首先检查它的所有相邻顶点，再依次访问它相邻顶点的，在访问相邻顶点时，检查其所有相邻顶点，重复这个过程直到找到给定的第二个点。在调用顶点的过程中，依次保存各顶点，并对访问过的顶点进行标记，标记过的顶点不再进行重复访问，直到找到终点。若在一条路径中未找到终点，则递归返回上一个点后要更新路径，重复这个过程直到找到终点。举例如下：
要找到 A 到 E 的最短路径
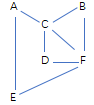
在这里插入图片描述
访问A，保存A
检查C，不是终点
检查E，是终点
访问E，保存A E
检查E，找到终点，结束

2、伪代码：

void chazhao(Graph* G,int v,int w,int* a,int n){ 
int t1,t2;
Q->enqueue(v);
G->setMark(v,VISITED); 
while(Q->length()!=0){ 
t1=Q->dequeue();
a[n++]=t1;
for(t2=G->first(t1);t2<G->n();t2++){ 
if(G->getMark(t2)==UNVISITED){
G->setMark(t2,VISITED); 
Q->enqueue(t2);
}
if(t2==w){
a[n]=t2; return;
}
}
}
}