11-1 算法性能评估

帖子：https://ceshiren.com/t/topic/10867

1）时间复杂度

• 规模:不同量级有不同的速度，比如水 vs 水杯: 水;规模大小对算法至关重要
• 测试环境：在不同测试环境，速度也不同，比如手机 vs 电脑: 电脑;运行环境：环境的快慢对算法至关重要

1.大O表示法

def tmp(n):
	add = 0
	for i in range(n):
		add += 1
	return add

运行 T(n) = (2n+1) * unit

算法的运行时间与数据规模成正比

T(n) = O(f(n)) O表示 T(n)与f(n)成正比

O表示渐近时间复杂度

表示代码执行时间随数据规模增长的变化趋势

当n很大时，低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略，就可以记为：T(n) = O(n); T(n) = O(n2)

只关注循环次数多的代码

def tmp(n):
	add = 0 
	for i in range(n)：
		add += i
	return add

O(n)

选大量级

def tmp(n):
    for i in range(999):
        print(123)

    for i in range(n):
        print(1)

    for i in range(n):
        for j in range(n):
            print(2)

O(n2)

嵌套循环要乘积

def tmp(n):
    for i in range(n):
        a(i)

def a(n):
    for i in range(n):
        print('c')

O(n2)

常见复杂度分析

• 非多项式量级（过于低效） : O(2n) 和 O(n!)。

• 多项式量级:O(1), O(logn), O(n), O(nlogn), O(nk)

O(1)

a=2
b=3
d=4

O(logn)

def tmp(n):
    i = 1
    while i < n :
        i = i * 2

i = 20,21, 22, 23…2x

退出循环的条件是 : 2x = n ,即 x = log2n，时间复杂度为 Ｏ(log2n)

def tmp(n):
    i = 1
    while i < n :
        i = i * 3

log3n 就等于 log32 * log3n，所以 O(log3n) = O(C * log2n)，其中 C=log32 是一个常量。基于我们前面的一个理论：在采用大 O 标记复杂度的时候，可以忽略系数，即 O(Cf(n)) = O(f(n))。所以，O(log2n) 就等于 O(log3n)。因此，在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为 O(logn)

O(m+n)、O(m*n)

def tmp(m, n):
    for i in range(m):
        print(1)

    for i in range(n):
        print(2)

2）空间复杂度

• 渐进时间复杂度：表示算法的执行时间与数据规模之间的增长关系。
• 渐进空间复杂度（asymptotic space complexity）：表示算法的存储空间与数据规模之间的增长关系。

def tmp(n):
    a = [1]*n
    for i in a:
        print(i)

空间复杂度是： O(n)

11-2 数组与列表

课程贴：https://ceshiren.com/t/topic/10895

1)什么是数组？

数组是线性表数据结构。用连续的内存空间存储相同类型的数据。

• 线性表：线性表是数据排成一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。
  包括：数组，链表、队列、栈。
• 非线性表：数据之间并不是简单的前后关系。
  包括：二叉树、堆、图等。
• 连续的内存空间和相同类型的数据：使数组支持“随机访问”。但在数组中删除、插入数据时，需要做大量的数据搬移工作。

数组如何实现随机访问？

C 语言代码： int[] tmp = new int[4]，这个数组在内存中连续放置：

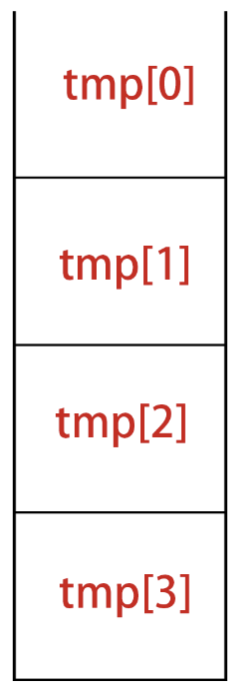
插入操作

• 在数组末尾插入元素，不需要移动数据，时间复杂度为 O(1)。
• 在数组开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)。
• 假设每个位置插入元素概率相同，平均情况时间复杂度为 (1+2+…n)/n=O(n)。
  
  如果元素无序，可直接换位：

删除操作

• 删除数组末尾数据：则最好情况时间复杂度为 O(1)；
• 删除开头的数据：则最坏情况时间复杂度为 O(n)；
• 平均情况时间复杂度也为 O(n)。
  

预删除思想：JVM 标记清除垃圾回收算法

2)改进数组

编程语言封装了数组，比如 Java 的 ArrayList， Python 的 List ，可实现自动扩容，多种数据类型组合。

如果你是底层工程师，需要极致的比如开发网络框架，性能的优化需要做到极致，这个时候数组就会优于容器，成为首选。

class Array:
    def __init__(self, capacity) -> None:
        self.data = [-1]*capacity
        # 记录存了多少数据
        self.count = 0
        # 数组容量
        self.n = capacity

    def insert(self, location, value):
        if self.n == self.count:
            return False

        if location < 0 or location > self.count:
            return False

        for i in range(self.count, location, -1):
            self.data[i] = self.data[i-1]
        
        self.data[location] = value
        self.count += 1
        return True

    def find(self, location):
        if location < 0 or location >= self.count:
        	# -1代表没找到
            return -1
        
        return self.data[location]
    

    
    def delete(self, location):
        if location < 0 or location >= self.count:
            return False
        
        for i in range(location + 1, self.count):
            self.data[i-1] = self.data[i]
        
        self.count -= 1
        return True
    
        

def test_demo():
    array = Array(5)
    array.insert(0, 1)
    array.insert(0, 2)
    array.insert(1, 3)
    array.insert(2, 4)
    array.insert(4, 5)
    
    # 判断插入不成功
    assert not array.insert(0, 100)
    assert array.find(0) == 2
    assert array.find(2) == 4
    assert array.find(4) == 5
    assert array.find(10) == -1
    assert array.count == 5
    removed = array.delete(4)
    assert removed
    assert array.find(4) == -1
    removed = array.delete(10)
    assert not removed
    # 2 3 4 1 5
    assert array.data == [2, 3, 4, 1, 5]

if __name__ == '__main__':
    test_demo()

• delete
  

python list 源码解析
本篇文章描述了 CPython 中 list 的实现方式。

3)C 语言用结构体表示 List 对象

C 语言使用结构体实现 list 对象，结构体代码如下。

typedef struct {
    PyObject_VAR_HEAD
    PyObject **ob_item; //指向 list 中的对象
    Py_ssize_t allocated; //内存分配的插槽
} PyListObject;

List 初始化
以 I = [] 为例

list 的数量是指 len(l)。分配的槽位数量是指在内存中实际分配的数量。通常情况，内存中分配的数量要大于 list 的数量。这是为了当添加新元素时，避免内存再分配。

Append

当运行l.append(1)时， CPython 将调用app1()：

list_resize() 会故意分配更多的内存，避免被多次调用。分配内存大小增加：0, 4, 8, 16, 25, 35, 46, 58, 72, 88, …

第一次分配了 4 个槽位，I[0] 指向了数字对象 1 。正方形虚线表示未使用过的槽位。追加操作的均摊复杂度为 O(1) 。

均摊时间复杂度是平均时间复杂度的一种，是一种简化的计算方法。

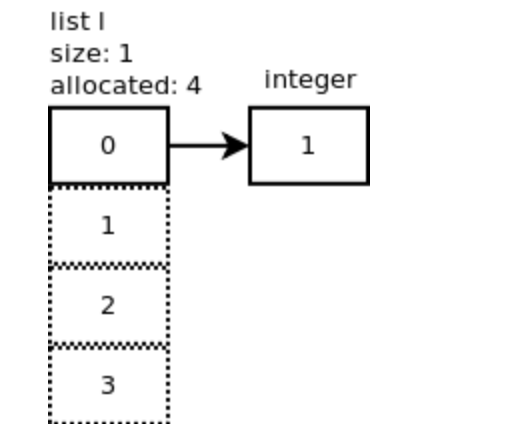
继续追加元素：l.append(2)。调用 list_resize 实现 n + 1 = 2。由于分配了四个空间，不需要分配内存。当再向列表追加两个数字时，l.append(3), l.append(4)，如下图如示：

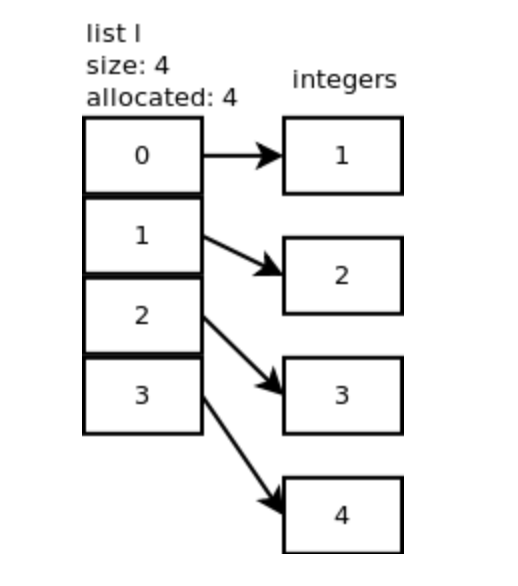
Insert

在位置 1 插入整型 5 ，即调用 python 的 l.insert(1, 5) 。CPython 会调用 ins1() ：

插入操作需要将剩余元素向右迁移：

上图虚线表示未使用的槽位（slots），分配了 8 个槽位，但 list 的长度只有 5 。 insert 的时间复杂度为 O(n)。

pop

弹出列表的最后一个元素使用 l.pop()，CPython 使用 listpop() 实现这个过程。如果新内存大小少于分配大小的一半， listpop() 将调用 list_resize 减少 list 内存。

Pop 的时间复杂度是 O(1)。

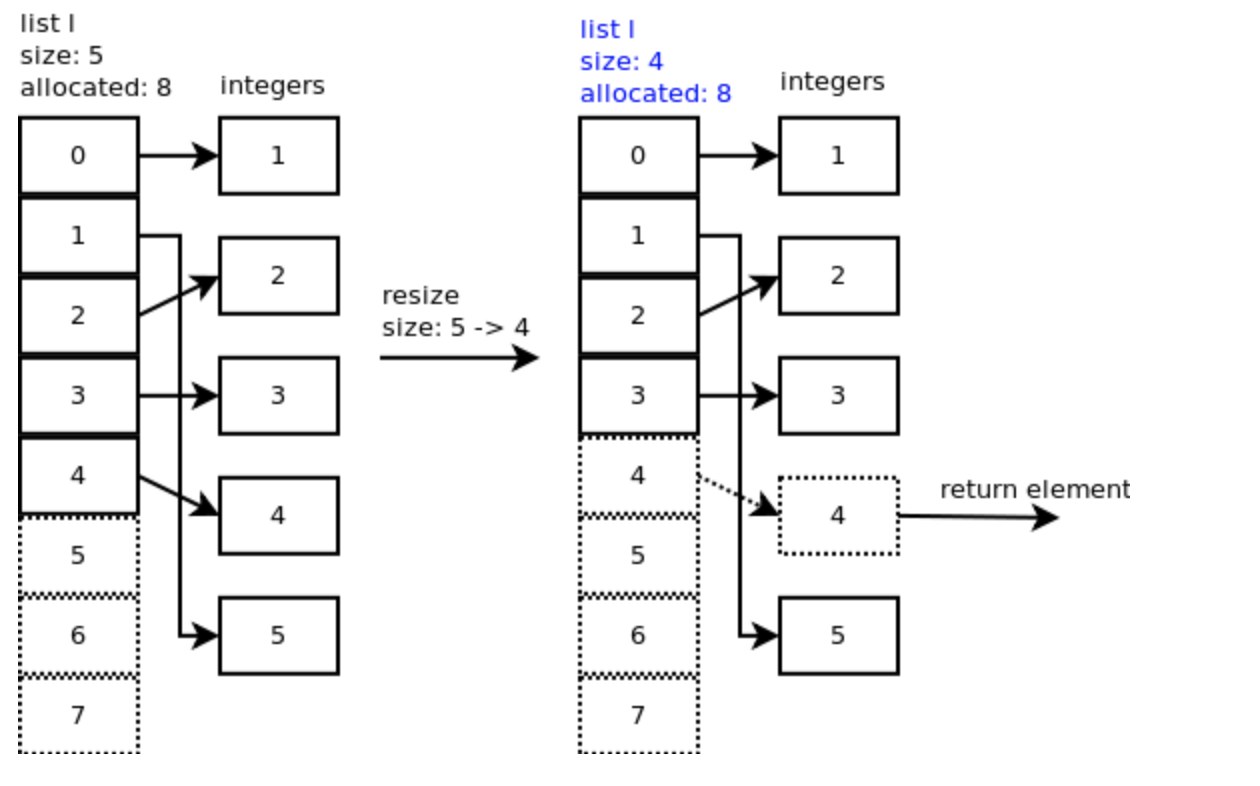
注意，此时槽位 4 仍然指向整型 4 ，但是 list 的大小却是 4 。只有 pop 更多的元素才能调用 list_resize() 减少内存，如果再 pop 一个元素， size - 1 = 4 - 3 = 3， 3 小于分配槽位的一半 8/2 = 4 。所以 list 收缩到 6 个槽位， list 的大小为 3 。虽然槽位 3 和 4 依旧指向整型对象，但是整体大小变成了 3 。

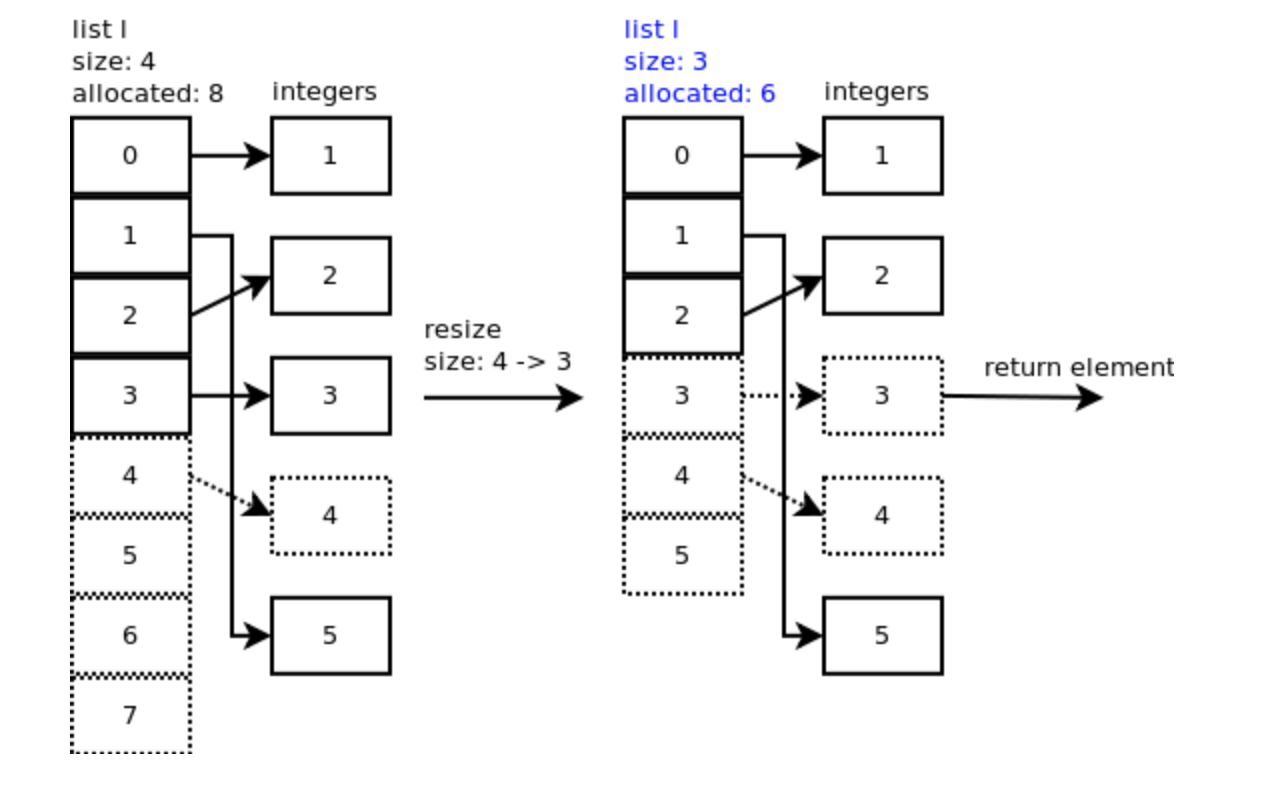
remove

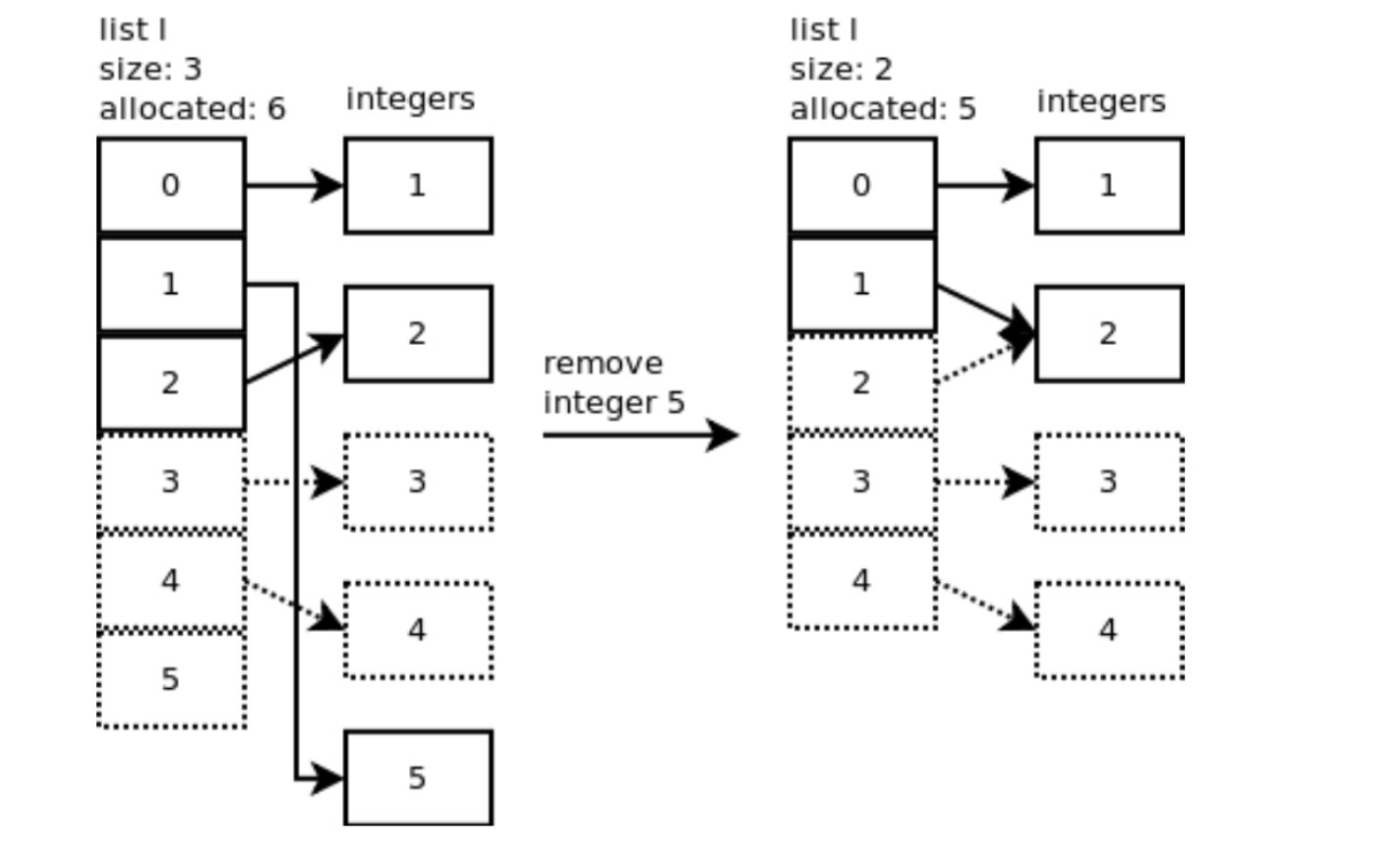
Python 可以用 remove 删除指定元素：l.remove(5)。此时将调用 listremove() 。

CPython 调用 list_ass_slice() 函数对列表进行切分并删除元素。当在位置 1 移除元素 5 时，低偏移（low offset）是 1 ，高偏移（high offset）是 2 ：

remove 时间复杂度是 O(n)。

文章参考：

http://www.laurentluce.com/posts/python-list-implementation/

11-3 队列

课程贴：https://ceshiren.com/t/topic/11369

知识前提

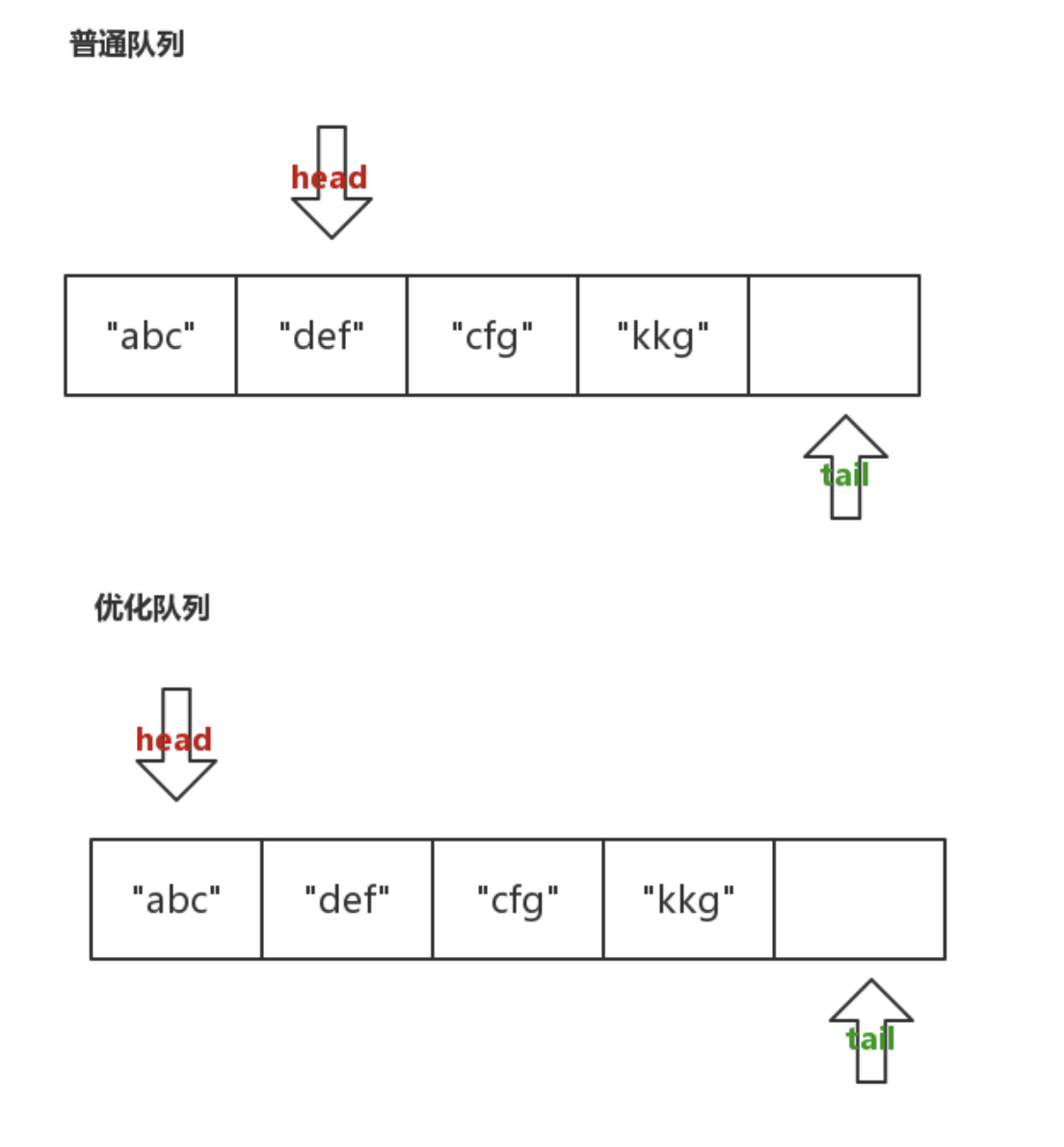
利用数组实现

普通队列
优化队列
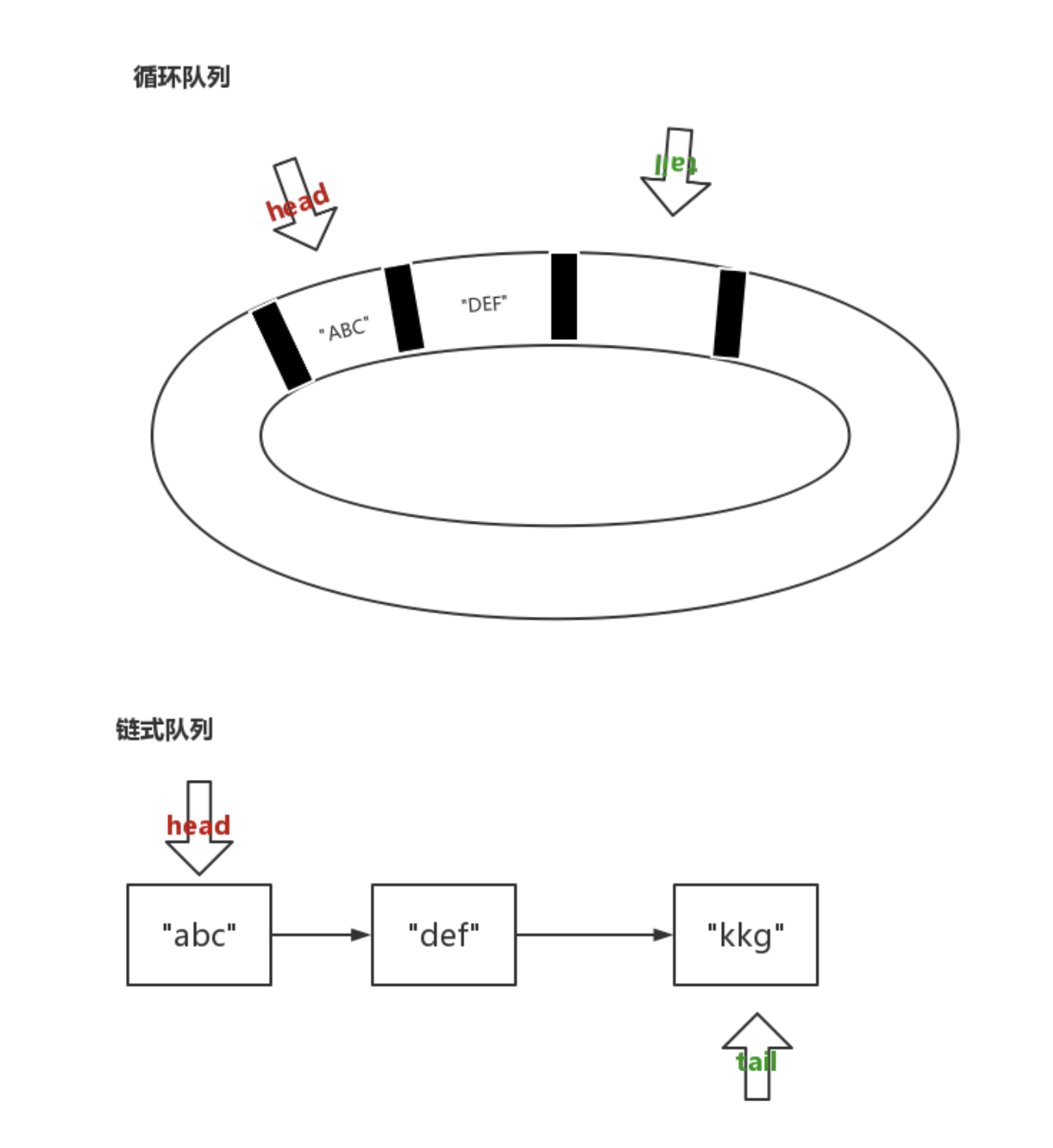
循环队列

利于优化

利用链表实现
普通链表队列

不易优化

队列二要素：入队，出队

头结点：

• 删除指定位置元素

• 判断队列是否为空
  尾结点：

• 指定新元素的插入位置

• 通过尾结点判断队列是否满了，如果满了，就禁止插入

• 判断队列是否为空

顺序队列

基础队列

Java

public class Queue {
    int n = 0;
    String[] items;
    int head;
    int tail;

    public Queue(int capacity) {
        n = capacity;
        items = new String[capacity];
    }

    public boolean enqueue(String item) {
        //如果队列满
        if (tail == n) return false;
        items[tail++] = item;
        return true;
    }

    public String dequeue() {
        if (head == tail) return null;
        return items[head++];
        
    }

    public static void main(String[] args) {
        Queue a = new Queue(10);
        a.enqueue("10");
        a.enqueue("20");
        String dequeItem = a.dequeue();
        System.out.println(dequeItem.equals("10"));
        a.enqueue("30");
        System.out.println(a.items[a.head].equals("20"));
        System.out.println(a.items[a.tail - 1].equals("30"));
        
    }
}

Python

class Queue:
    def __init__(self, capacity: int) -> None:
        self.n = capacity
        self.items = [-1]*capacity
        self.head = 0
        self.tail = 0

    def enqueue(self, data):
        if self.n == self.tail:
            return False
        self.items[self.tail] = data
        self.tail += 1
        return True

    def dequeue(self):
        if self.head == self.tail:
            return None
        value = self.items[self.head]
        self.head += 1
        return value


def test_queue():
    a = Queue(10)
    a.enqueue("10")
    a.enqueue("20")
    deque_item = a.dequeue()
    assert deque_item == "10"
    a.enqueue("30")
    assert a.items[a.head] == "20"
    assert a.items[a.tail - 1] == "30"


if __name__ == "__main__":
    test_queue()

加入数据迁移的队列

上一种队列会越用越小，就需要对数据进行迁移，实现队列的自动整理。
Java

public class Queue {
    private String[] items;
    private int n = 0;
    private int head = 0;
    private int tail = 0;

    public tmp(int capacity) {
        n = capacity;
        items = new String[n];
    }

    public boolean enqueue(String item) {
        if (tail == n) {
            if (head == 0) return false;
            for (int i = head; i < tail; ++i) {
                items[i-head] = items[i];
            }
            tail -= head;
            head = 0;
        }
        items[tail] = item;
        ++tail;
        return true;
    }

    public String dequeue() {
        if (head == tail)
            return null;
        return items[head++];
    }

    public static void main(String[] args) {
        Queue a = new Queue(3);
        a.enqueue("10");
        a.enqueue("20");
        a.enqueue("30");
        boolean result = a.enqueue("40");
        System.out.println(!result);
        String dequeItem = a.dequeue();
        System.out.println(dequeItem.equals("10"));
        a.enqueue("30");
        System.out.println(a.items[0].equals("20"));
        System.out.println(a.items[2].equals("30"));

    }
}

Python

class Queue:
    def __init__(self, capacity: int) -> None:
        self.n = capacity
        self.items = [-1]*capacity
        self.head = 0
        self.tail = 0

    def enqueue(self, data):
        if self.n == self.tail:
            if self.head == 0:
                return False
            for i in range(self.head, self.tail):
                self.items[i-self.head] = self.items[i]
            self.tail -= self.head
            self.head = 0
        self.items[self.tail] = data
        self.tail += 1
        return True

    def dequeue(self):
        if self.head == self.tail:
            return None
        value = self.items[self.head]
        self.head += 1
        return value


def test_queue():
    a = Queue(3)
    a.enqueue("10")
    a.enqueue("20")
    a.enqueue("30")
    result = a.enqueue("40")
    assert not result
    deque_item = a.dequeue()
    assert deque_item == "10"
    a.enqueue("30")
    assert a.items[0] == "20"
    assert a.items[2] == "30"


if __name__ == "__main__":
    test_queue()

链式队列

Java

public class Queue {
    Node head = null;
    Node tail = null;
    public void enqueue(String item) {
        if (tail == null) {
            Node newNode = new Node(item);
            head = newNode;
            tail = newNode;
        }else {
            tail.next = new Node(item);
            tail = tail.next;
        }
    }

    public String dequeue() {
        if (head == null) return null;
        String value = head.data;
        head = head.next;
        return value;
    }

    public static void main(String[] args) {
        Queue a = new Queue();
        a.enqueue("10");
        a.enqueue("20");
        a.enqueue("30");
        String dequeItem = a.dequeue();
        System.out.println(dequeItem == "10");
        System.out.println(a.head.data == "20");
        System.out.println(a.head.next.data == "30");

    }

    public static class Node {
        String data;
        Node next = null;
        public Node(String data) {
            this.data = data;
        }

    }

}

Python

class Queue:
    def __init__(self) -> None:
        self.head = None
        self.tail = None

    def enqueue(self, data):
        if self.tail is None:
            new_node = self.Node(data)
            self.tail = new_node
            self.head = new_node
        else:
            self.tail.next = self.Node(data)
            self.tail = self.tail.next
        
       

    def dequeue(self):
        if self.head is None:
            return None
        value = self.head.data
        self.head = self.head.next
        return value



    class Node:
        def __init__(self, data) -> None:
            self.data = data
            self.next = None


def test_queue():
    a = Queue()
    a.enqueue("10")
    a.enqueue("20")
    a.enqueue("30")
    deque_item = a.dequeue()
    assert deque_item == "10"
    assert a.head.data == "20"
    assert a.head.next.data == "30"


if __name__ == "__main__":
    test_queue()

循环队列

Java

public class Queue {
    int n = 0;
    String[] items;
    int head = 0;
    int tail = 0;

    public Queue(int capacity) {
        n = capacity;
        items = new String[capacity];

    }

    public boolean enqueue(String item) {
        if ((tail + 1) % n == head)
            return false;
        items[tail] = item;
        tail = (tail + 1) % n;
        return true;

    }

    public String dequeue() {
        if (head == tail)
            return null;
        String value = items[head];
        head = (head + 1) % n;
        return value;
    }

    public static void main(String[] args) {
        Queue a = new Queue(3);
        a.enqueue("10");
        a.enqueue("20");
        boolean result = a.enqueue("30");
        // 循环队列需要空出一格
        System.out.println(!result);
        String dequeItem = a.dequeue();
        a.enqueue("30");
        System.out.println(a.items[2] == "30");
        result = a.enqueue("10");
        System.out.println(result == false);

    }

}

Python

class Queue:
    def __init__(self, capacity) -> None:
        self.head = 0
        self.tail = 0
        self.n = capacity
        self.items = [-1]*capacity

    def enqueue(self, data):
        if (self.tail + 1) % self.n == self.head:
            return False
        self.items[self.tail] = data
        self.tail = (self.tail + 1) % self.n
        return True

    def dequeue(self):
        if self.tail == self.head:
            return None
        value = self.items[self.head]
        self.head = (self.head + 1) % self.n
        return value


def test_queue():
    a = Queue(3)
    a.enqueue("10")
    a.enqueue("20")
    result = a.enqueue("30")
    assert not result
    a.dequeue()
    a.enqueue("30")
    assert a.items[2] == "30"
    result = a.enqueue("10")
    assert not result


if __name__ == "__main__":
    test_queue()

阻塞队列

入队和出队可以等待

并发队列

支持多线程的阻塞队列

11-4 堆栈

课程贴：https://ceshiren.com/t/topic/11592

引言

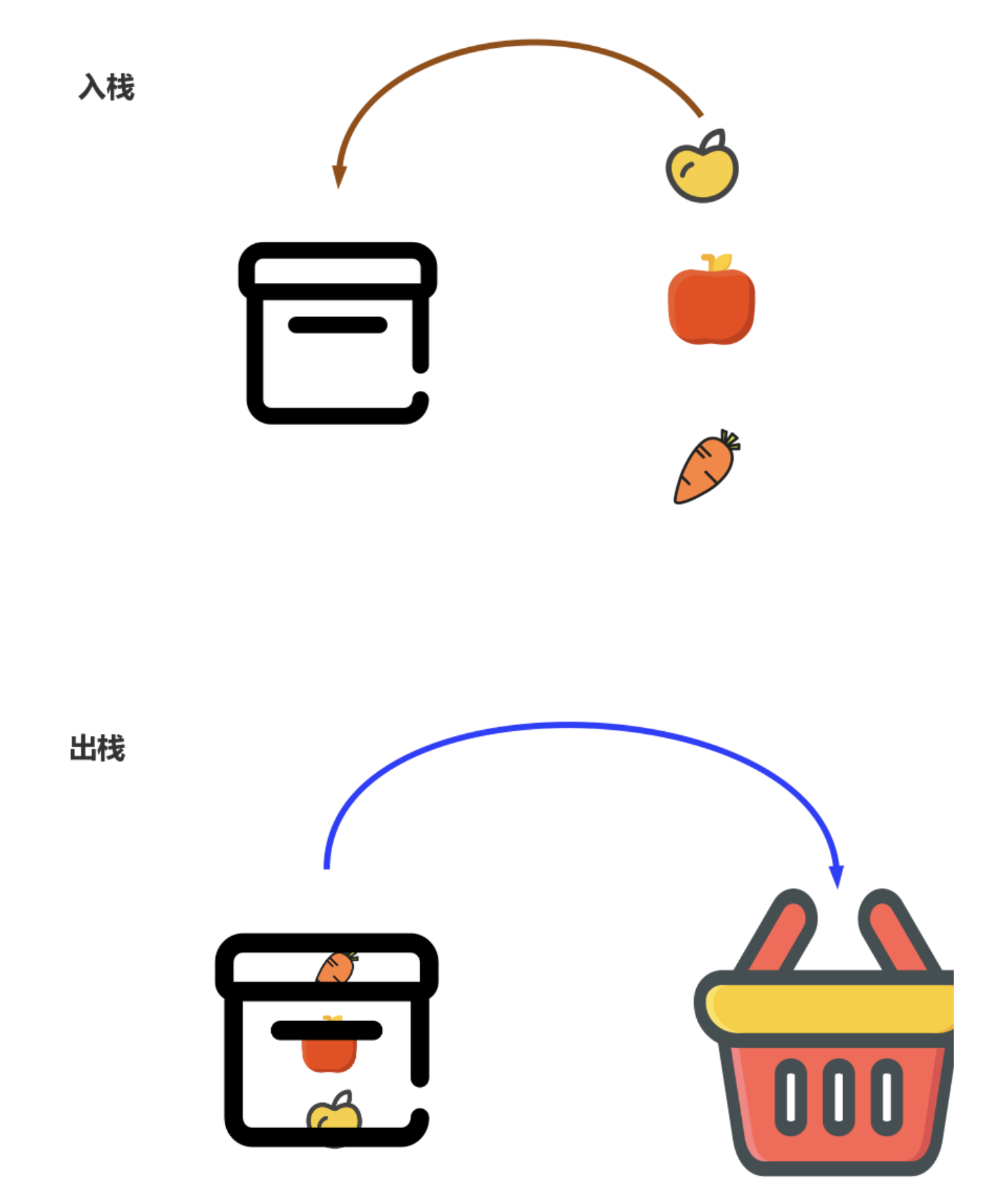
• 函数调用
• 编译原理：语法分析
• 括号匹配

问题：栈是操作受限的线性表，为什么不直接用数组或者链表？

数组和链表暴露了太多接口，操作虽然灵活，但不可控，容易出错。比如数组支持任意位置插入数组，如果插入位置写错将改变所有数组的内容。

而栈只能在一端插入和删除数据，并且后进先出。

顺序栈

使用数组实现栈

class ArrayStack:
    def __init__(self, n) -> None:
        self.data = [-1]*n
        self.n = n
        self.count = 0
    
    def push(self, value):
        if self.n == self.count:
            return False
        self.data[self.count] = value
        self.count += 1
        return True
    
    def pop(self):
        if self.count == 0:
            return None

        self.count -= 1
        return self.data[self.count]

def test_static():
    array_stack = ArrayStack(5)
    data = ["a", "b", "c", "d", "e"]
    for i in data:
        array_stack.push(i)

    result = array_stack.push("a")
    assert not result
    data.reverse()
    for i in data:
        assert i == array_stack.pop()

    assert array_stack.pop() is None

if __name__ == '__main__':
    test_static()

入栈时间复杂度：O(1)
出栈时间复杂度：O(1)

链式栈

使用链表实现栈

class StackBasedOnLinkedList:
    def __init__(self) -> None:
        self.top = None

    def push(self, value):
        new_node = self.Node(value)
        if self.top is None:
            self.top = new_node
        else:
            new_node.next = self.top
            self.top = new_node

    def pop(self):
        if self.top is None:
            return -1
        result = self.top.data
        self.top = self.top.next
        return result

    class Node:
        def __init__(self, data) -> None:
            self.data = data
            self.next = None


def test_static():
    stack = StackBasedOnLinkedList()
    data = [1, 2, 3, 4, 5]
    for i in data:
        stack.push(i)
    data.reverse()
    for i in data:
        assert i == stack.pop()
    assert stack.pop() == -1

入栈时间复杂度：O(1)
出栈时间复杂度：O(1)

11-5 链表

课程贴：https://ceshiren.com/t/topic/11561

链表与数组的区别

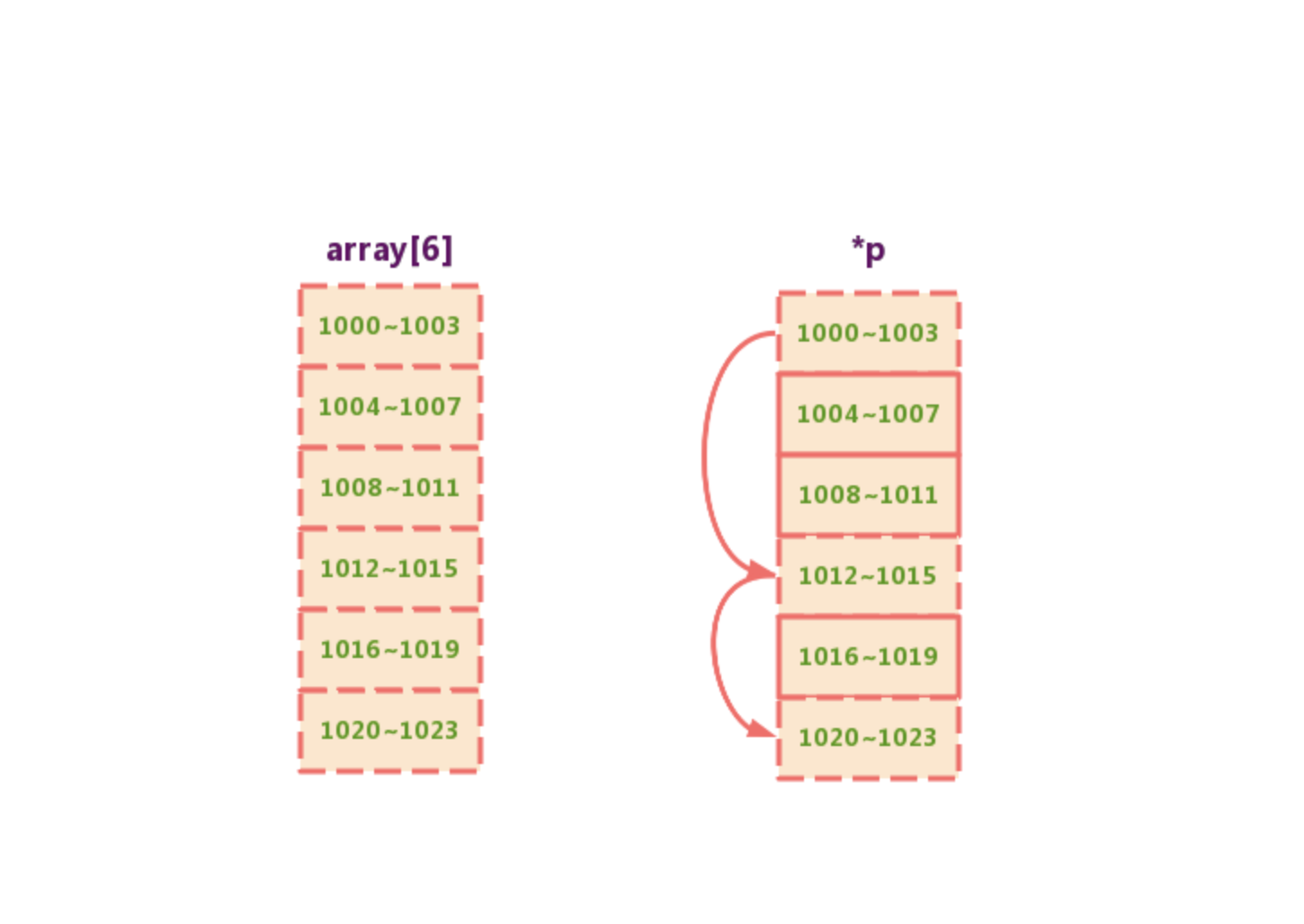
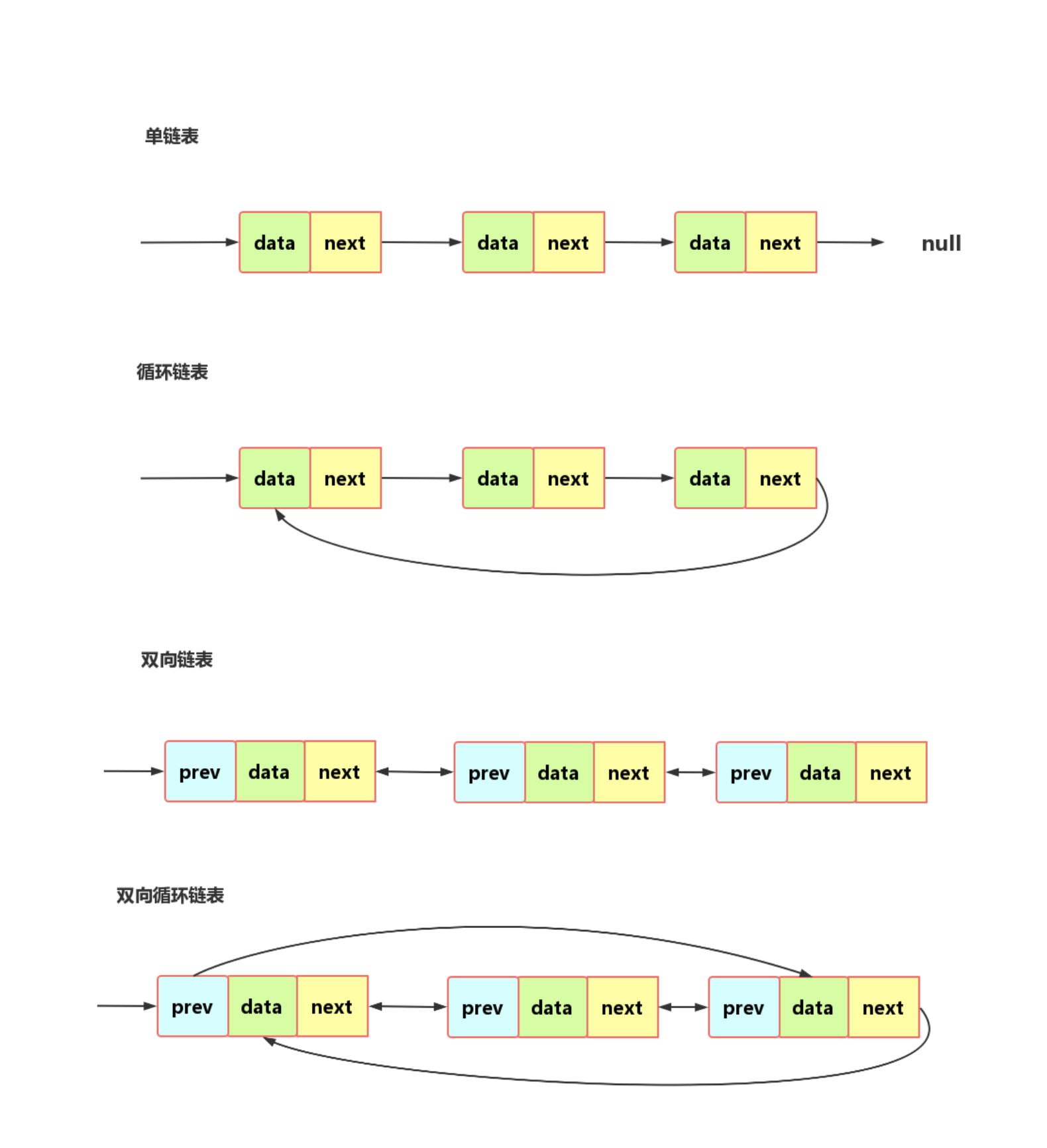
单链表与循环链表

注意链表中的头结点和尾结点。

循环链表从尾可以方便的到头，适合环型结构数据，比如约瑟夫问题。

双向链表

优势：

O(1) 时间复杂度找到前驱结点

删除，插入更高效。考虑以下两种情况：

• 删除结点中“值等于某个给定值”的结点
• 删除给定指针指向的结点

查询更高效：记录上次查找的位置 p，每次查询时，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据。

再次比较数组和链表

从复杂度分析：

时间复杂度	数组	链表
插入删除	O(n)	O(1)
随机访问	O(1)	O(n)

其它角度：

• 内存连续，利用 CPU 的缓存机制，预读数组中的数据，所以访问效率更高。

• 而链表在内存中并不是连续存储，所以对 CPU 缓存不友好，没办法有效预读。

• 数组的大小固定，即使动态申请，也需要拷贝数据，费时费力。

• 链表支持动态扩容.

class SinglyLinkedList:
    def __init__(self) -> None:
        self.head = None

    def insert_tail(self, value):
        if self.head is None:
            self.insert_to_head(value)
            return
        q = self.head
        # 寻找尾结点
        while q.next is not None:
            q = q.next
        new_node = self.Node(value)
        q.next = new_node

    def insert_to_head(self, value):
        new_node = self.Node(value)
        if self.head is None:
            self.head = new_node
        else:
            new_node.next = self.head
            self.head = new_node

    def delete_by_value(self, value):
        if self.head is None:
            return False
        q = self.head
        p = None
        while q is not None and q.data != value:
            p = q
            q = q.next
        # 当链表中没有 value 的时候
        if q is None:
            return False
        # head 的值就是 value 的时候
        if p is None:
            self.head = self.head.next
        else:
            p.next = q.next
        return True

    def find_by_value(self, value):
        if self.head is None:
            return
        q = self.head
        while q is not None and q.data != value:
            q = q.next

        if q is None:
            return
        return q

    def insert_after(self, node, value):
        if node is None:
            return
        new_node = self.Node(value)
        new_node.next = node.next
        node.next = new_node

    def insert_before(self, node, value):
        if self.head is None:
            self.insert_to_head(value)
            return
        q = self.head
        while q is not None and q.next != node:
            q = q.next
        # 链表中，没有一个与 node 相等的结点
        if q is None:
            return
        new_node = self.Node(value)
        new_node.next = node
        q.next = new_node
        



    def print_all(self):
        if self.head is None:
            return
        q = self.head
        while q is not None:
            print(q.data)
            q = q.next

    class Node:
        def __init__(self, data) -> None:
            self.data = data
            self.next = None


def test_link():
    link = SinglyLinkedList()
    data = [1, 2, 5, 3, 1]
    for i in data:
        link.insert_tail(i)
    link.insert_to_head(99)
    # 打印内容为 99 1 2 5 3 1
    link.print_all()
    link.delete_by_value(2)
    assert not link.delete_by_value(999)
    assert link.delete_by_value(99)
    # 打印内容为 1 5 3 1
    link.print_all()
    assert link.find_by_value(2) is None
    new_node = link.find_by_value(3)
    link.insert_after(new_node, 10)
    assert link.find_by_value(3).next.data == 10
    link.insert_before(new_node, 30)
    assert link.find_by_value(5).next.data == 30


if __name__ == '__main__':
    test_link()

public class SinglyLinkedList {
    Node head;

    public void insertTail(int value) {
        if (head == null) {
            insertToHead(value);
            return;
        }
        Node q = head;
        while (q.next != null) {
            q = q.next;
        }
        Node newNode = new Node(value);
        q.next = newNode;

    }

    public void insertToHead(int value) {
        Node newNode = new Node(value);
        newNode.next = head;
        head = newNode;

    }

    public boolean deleteByValue(int value) {
        if (head == null)
            return false;

        Node p = head;
        Node q = null;
        while (p != null && p.data != value) {
            q = p;
            p = p.next;
        }
        // 链表中，没有 value
        if (p == null)
            return false;
        // 数据在 head 上
        if (q == null) {
            head = head.next;
        } else {
            q.next = p.next;
        }
        return true;

    }

    public Node findByValue(int value) {
        if (head == null)
            return null;
        Node q = head;
        while (q != null && q.data != value) {
            q = q.next;
        }
        if (q == null)
            return null;

        return q;
    }

    public void insertAfter(Node node, int value) {
        if (node == null)
            return;

        Node newNode = new Node(value);
        newNode.next = node.next;
        node.next = newNode;

    }

    public void insertBefore(Node node, int value) {
        if (node == null)
            return;
        if (head == null) {
            insertToHead(value);
        } else {
            Node q = head;
            while (q != null && q.next != node) {
                q = q.next;
            }
            if (q == null)
                return;
            Node newNode = new Node(value);
            newNode.next = q.next;
            q.next = newNode;
        }

    }

    public void printAll() {
        if (head == null)
            return;
        Node q = head;
        while (q != null) {
            System.out.print(q.data + "  ");
            q = q.next;
        }
        System.out.println();
    }

    public static class Node {
        int data;
        Node next;

        public Node(int data) {
            this.data = data;
        }
    }

    public static void main(String[] args) {
        SinglyLinkedList link = new SinglyLinkedList();
        int data[] = { 1, 2, 5, 3, 1 };
        for (int i = 0; i < data.length; i++) {
            link.insertTail(data[i]);
        }
        link.insertToHead(99);
        // 打印内容为 99 1 2 5 3 1
        link.printAll();
        link.deleteByValue(2);
        System.out.println(!link.deleteByValue(999));
        System.out.println(link.deleteByValue(99));
        // 打印内容为 1 5 3 1
        link.printAll();
        System.out.println(link.findByValue(2) == null);
        Node newNode = link.findByValue(3);
        link.insertAfter(newNode, 10);
        System.out.println(link.findByValue(3).next.data == 10);
        link.insertBefore(newNode, 30);
        System.out.println(link.findByValue(5).next.data == 30);

    }

}

11-6 二叉树

课程贴：https://ceshiren.com/t/topic/11728

树的基本术语

父节点，子节点： A 和Ｂ
兄弟节点：D E J
根节点：A
叶节点：G I

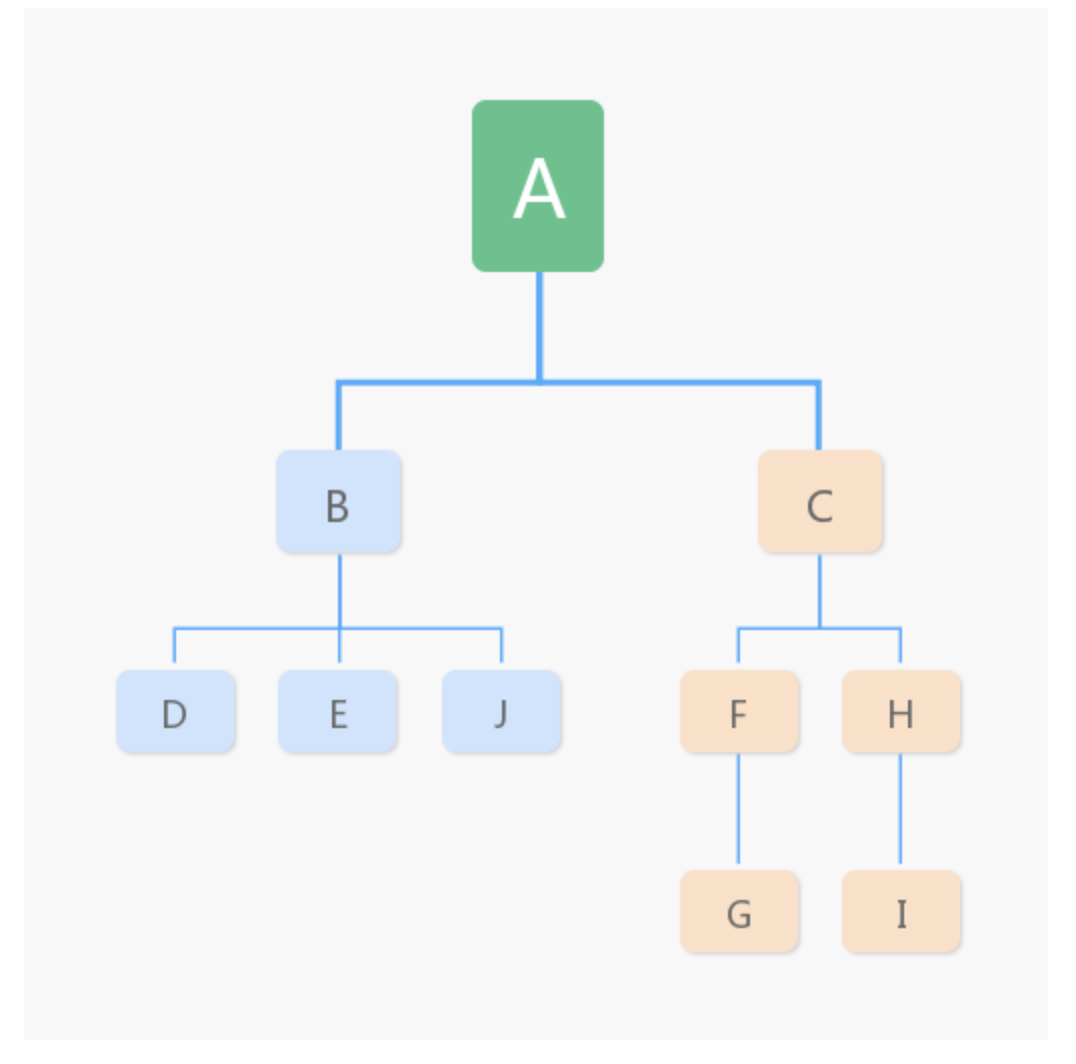
• 节点高度：节点到叶节点的最长路径（边数）

• 节点深度：根节点到这节点所经历的边的个数

• 节点的层数：节点的深度 + 1

• 树高度：根节点的高度
  

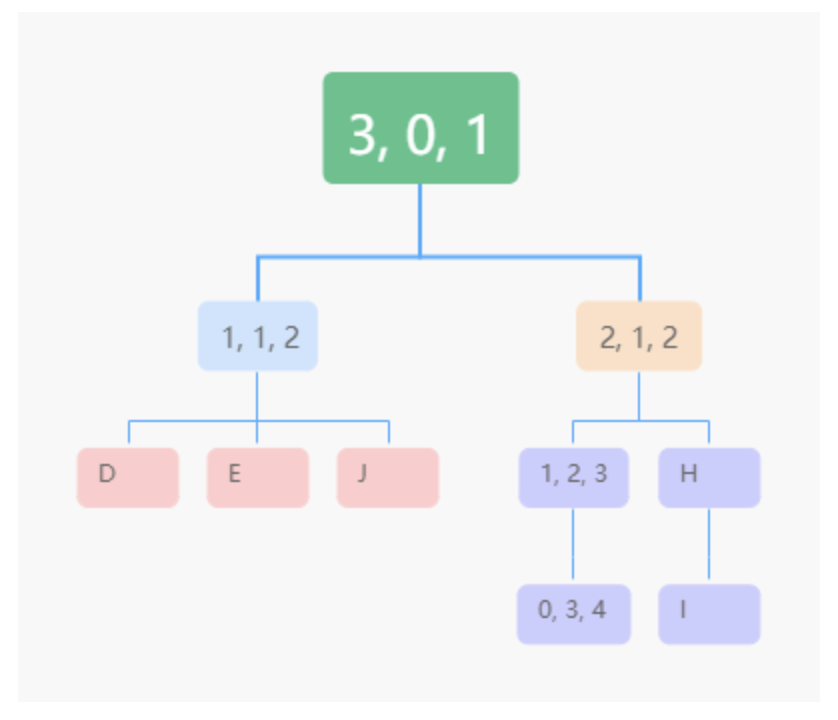
• 节点的高度：一个人量身体各部位长度，从脚下拉尺到各部位（腿长）

• 节点深度：量水中物品的深度，从水面拉尺到水中的宝藏

• 节点的层数：尺子从 1 开始计数

• 树高度：头到脚的高度

二叉树

最多有两个叉的树。

满二叉树：叶子节点全在最底层，除了叶子节点之外，每个节点都有左右两个子节点。

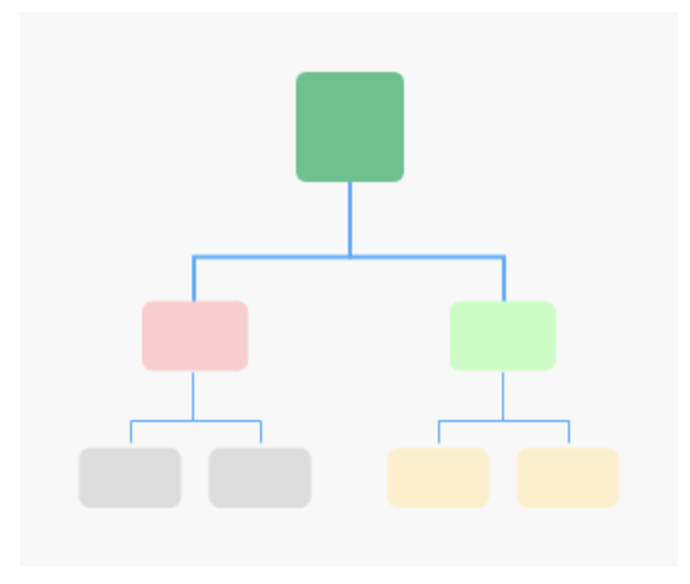
完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大。

满二叉树和完全二叉树的意义是什么？

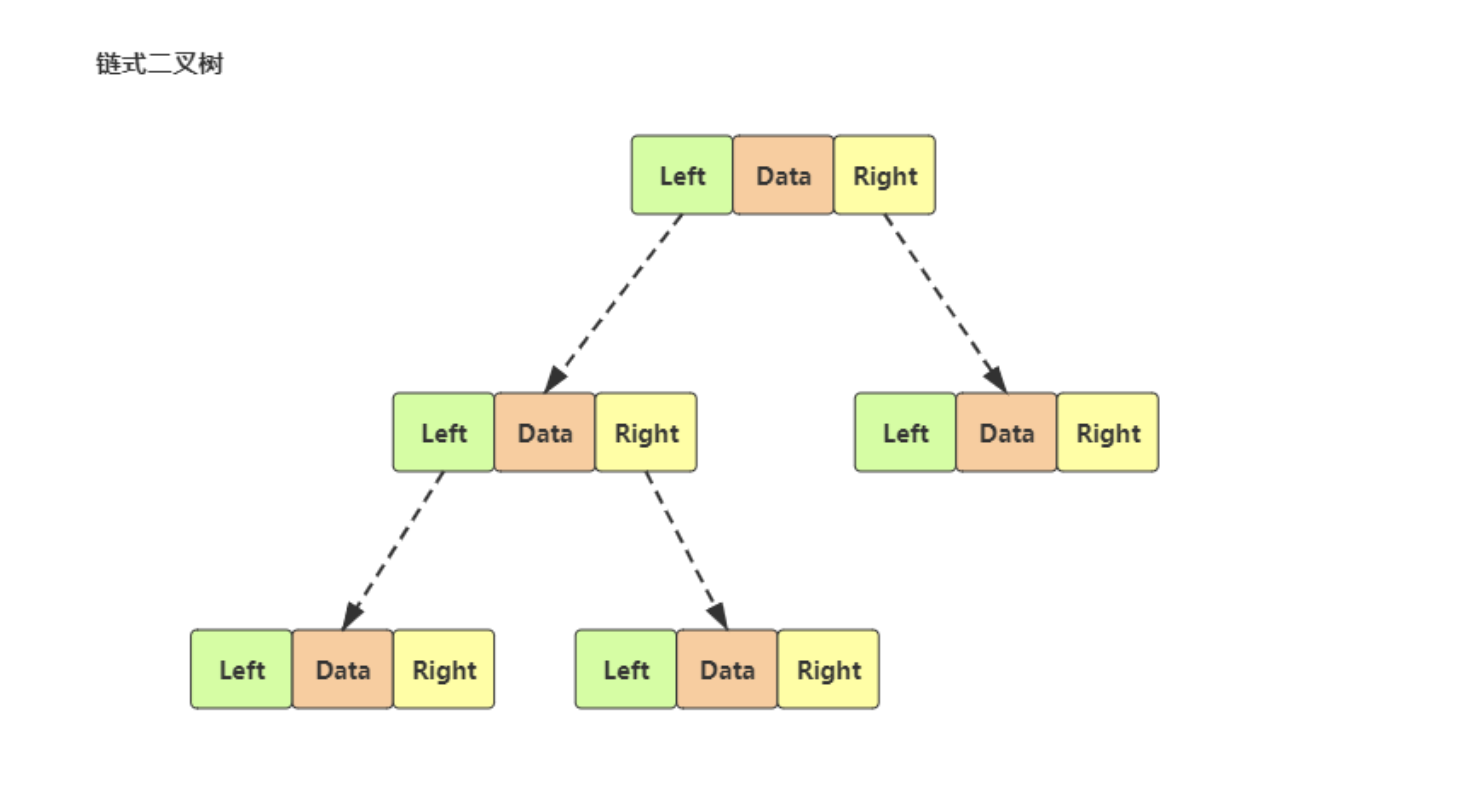
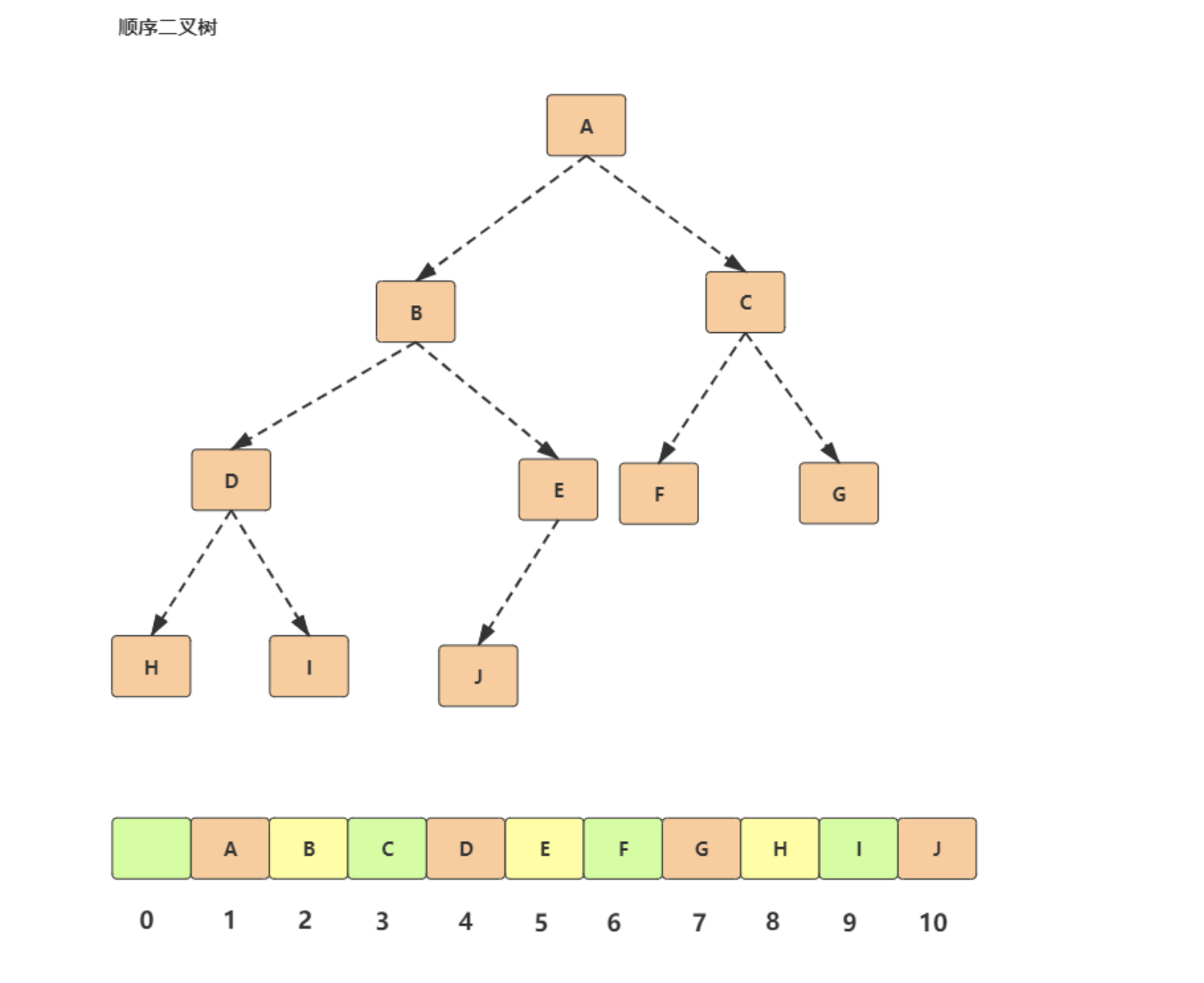
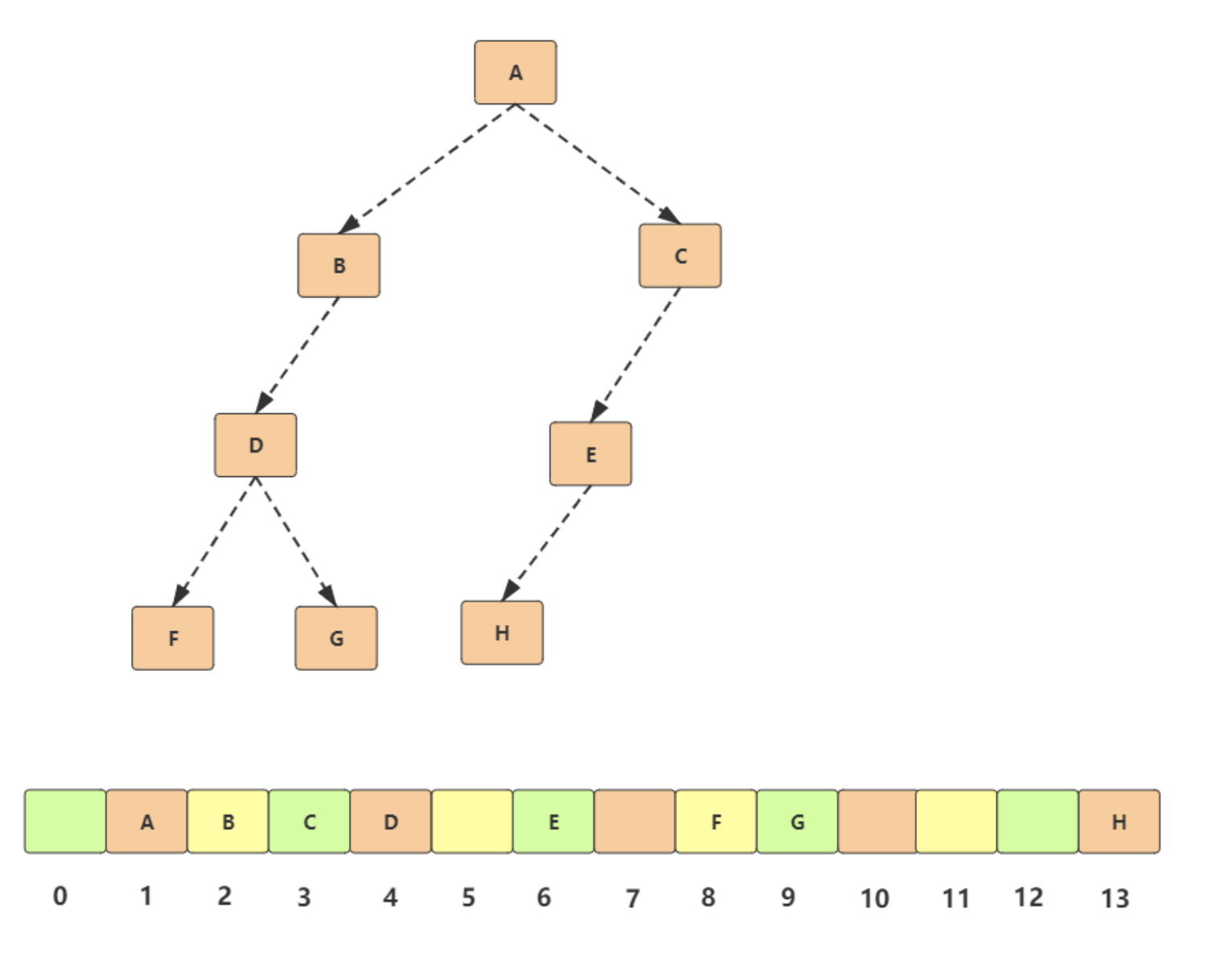
• 节点 X 在数组下标 i
• 左子节点：2 * i
• 右子节点：2 * i + 1
• 父节点：i/2

二叉树的遍历

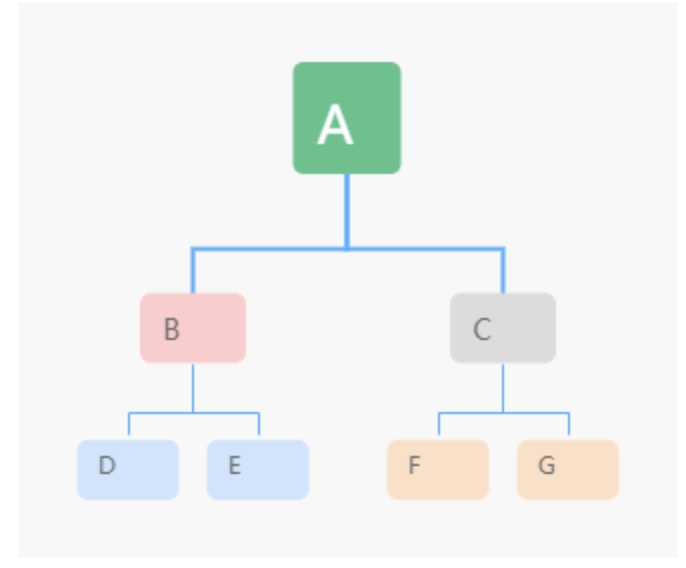
根据节点打印的顺序分前，中，后。比如：

• 前序遍历：节点 → 左子树 → 右子树。A->B->D->E->C->F->G
• 中序遍历：左子树 → 节点 → 右子树。D->B->E->A->F->C->G
• 后序遍历：左子树 → 右子树 → 节点。D->E->B->F->G->C->A

递推关系式：

前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

代码：

void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印root节点
  preOrder(root->left);
  preOrder(root->right);
}

void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印root节点
  inOrder(root->right);
}

void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印root节点
}

复杂度：

O(n)：遍历操作的时间复杂度，跟节点的个数 n 成正比

二叉查找树

左子树每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。

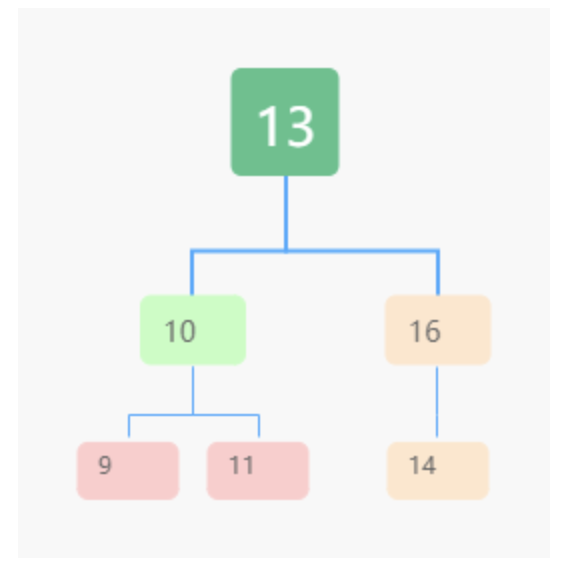
查找

根节点

• 比之小> 左子树中递归查找。
• 比之大> 右子树中递归查找。

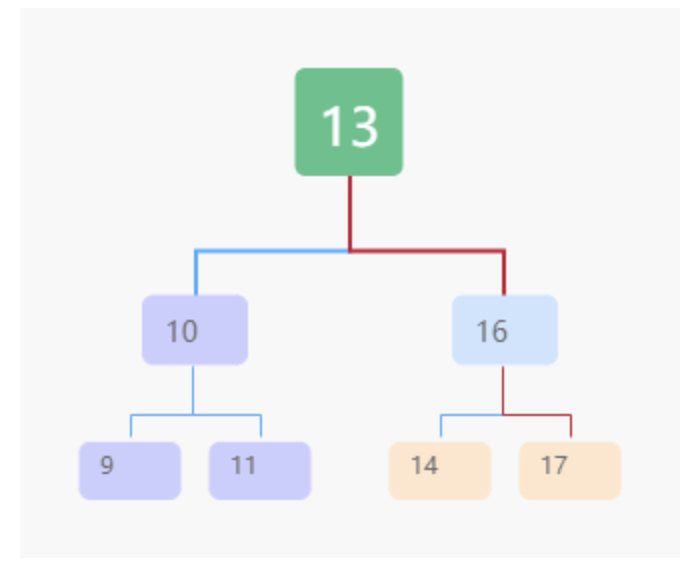
插入

• 从根节点开始比较，如果比之大，并且节点右子树为空，就将新数据插到右子节点；
• 如果不为空，就再递归遍历右子树，查找插入位置。
• 如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置。
• 如果不为空，就再递归遍历左子树，查找插入位置。
  

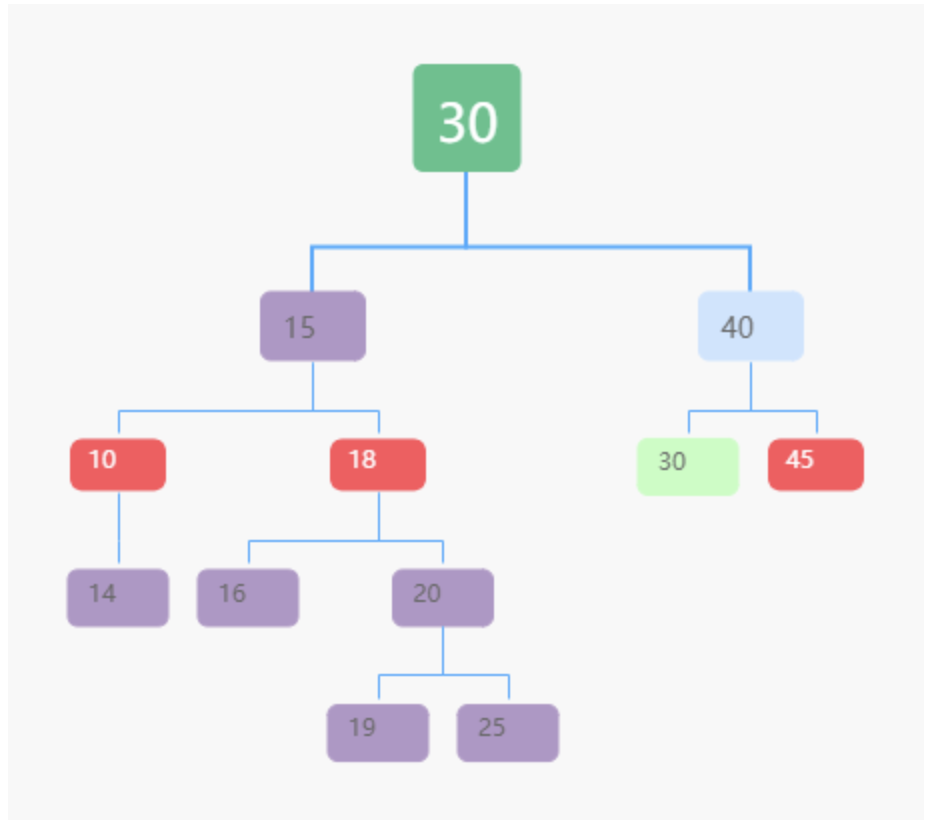
删除

情况一：要删除的节点没有子节点

只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 55。

情况二：如果要删除的节点只有一个子节点（只有左子节点或者右子节点），

只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。

情况三：如果要删除的节点有两个子节点

• 找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。

• 然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
  
  

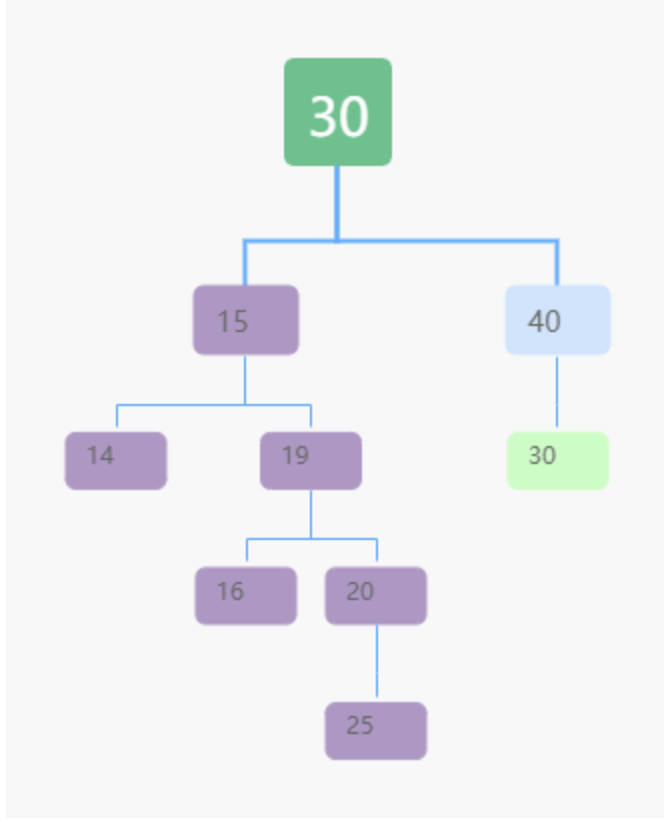
  取巧方法：将要删除的节点标记为“已删除”。

重要特性

中序遍历二叉查找树，可以得到有序的数据序列，时间复杂度是 O(n)。因此，二叉查找树又称二叉排序树。

class BinarySearchTree:
    def __init__(self) -> None:
        self.tree = None

    class Node:
        def __init__(self, data) -> None:
            self.data = data
            self.left = None
            self.right = None

    def insert(self, value):
        # 如果是根结点，直接插入
        if self.tree is None:
            self.tree = self.Node(value)
            return

        p = self.tree
        while p is not None:
            if value > p.data:
                if p.right is None:
                    p.right = self.Node(value)
                    return
                p = p.right
            elif value < p.data:
                if p.left is None:
                    p.left = self.Node(value)
                    return
                p = p.left

    def find(self, value):
        p = self.tree
        while p is not None:
            if value > p.data:
                p = p.right
            elif value < p.data:
                p = p.left
            else:
                return p
        return None

    def delete(self, value):
        p = self.tree
        pp = None
        while p is not None and p.data != value:
            pp = p
            if value > p.data:
                p = p.right
            elif value < p.data:
                p = p.left

        if p is None:
            return

        if p.left is not None and p.right is not None:
            tmp_p = p.right
            tmp_pp = p
            # 找要删除结点的右子树中的最小值
            while tmp_p.left is not None:
                tmp_pp = tmp_p
                tmp_p = p.left
            p.data = tmp_p.data
            p = tmp_p
            pp = tmp_pp

        if p.left is not None:
            child = p.left
        elif p.right is not None:
            child = p.right
        else:
            child = None

        # 删除根结点
        if pp is None:
            self.tree = child
        elif pp.left is p:
            pp.left = child
        elif pp.right is p:
            pp.right = child

    def pre_order(self, node):
        if node is None:
            return
        print(node.data)
        self.pre_order(node.left)
        self.pre_order(node.right)

    def in_order(self, node):
        if node is None:
            return
        self.in_order(node.left)
        print(node.data)
        self.in_order(node.right)

    def post_order(self, node):
        if node is None:
            return
        self.post_order(node.left)
        self.post_order(node.right)
        print(node.data)


def test_binary_search_tree():

    binary_search_tree = BinarySearchTree()
    data = [1, 10, 20, 40, 13]
    for i in data:
        binary_search_tree.insert(i)
    assert 20 == binary_search_tree.find(20).data
    binary_search_tree.delete(20)
    assert binary_search_tree.find(20) is None
    # 1 10 40 13
    binary_search_tree.pre_order(binary_search_tree.tree)
    print("-----------------------")
    # 1 10 13 40
    binary_search_tree.in_order(binary_search_tree.tree)
    print("-----------------------")
    # 13 40 10 1
    binary_search_tree.post_order(binary_search_tree.tree)


if __name__ == '__main__':
    test_binary_search_tree()

最后

以上就是单薄枫叶为你收集整理的11 数据结构、算法、设计模式11-1 算法性能评估11-2 数组与列表11-3 队列11-4 堆栈11-5 链表11-6 二叉树的全部内容，希望文章能够帮你解决11 数据结构、算法、设计模式11-1 算法性能评估11-2 数组与列表11-3 队列11-4 堆栈11-5 链表11-6 二叉树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。