运行结果演示

我将该论文发布于此处的代码进行了阅读与运行，得到结果如下：
训练过程（以CIFAR-10为例子使用VGG16模型进行训练）


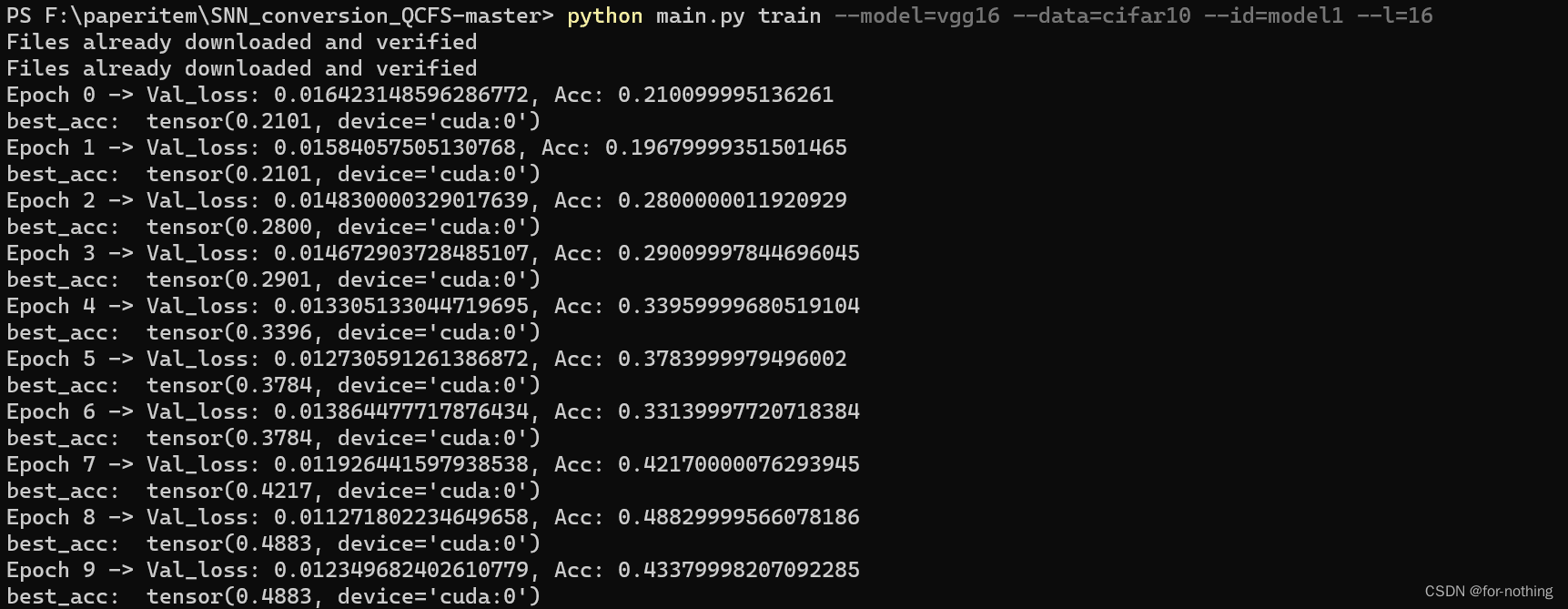
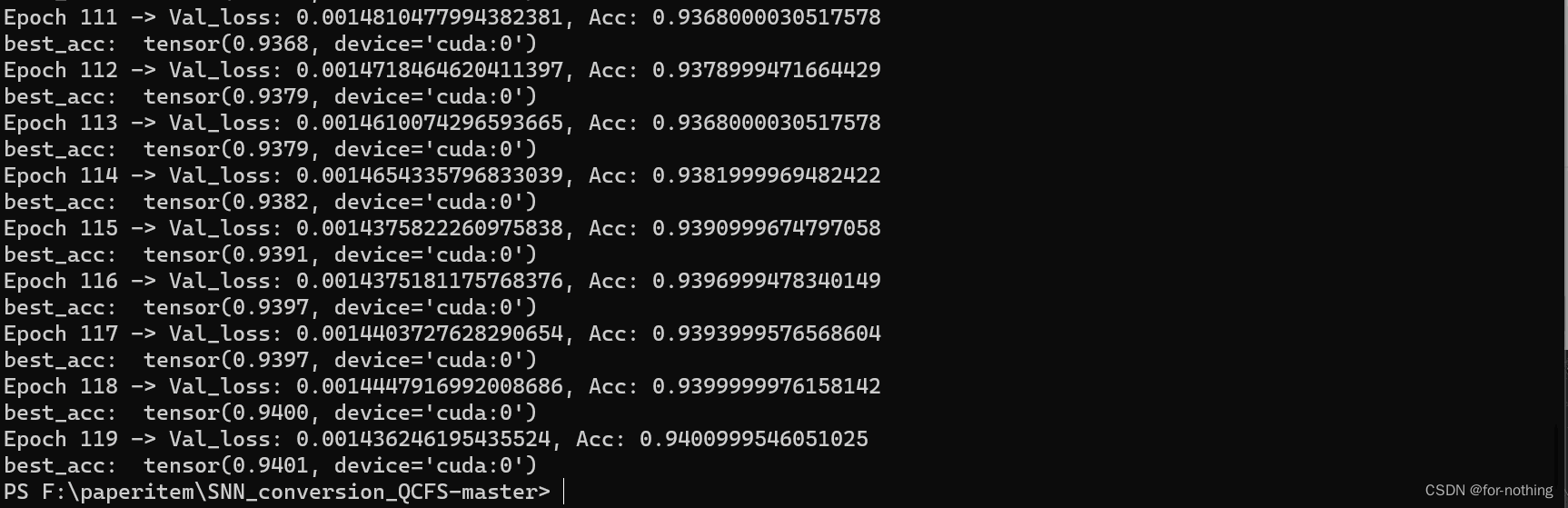
结果测试：

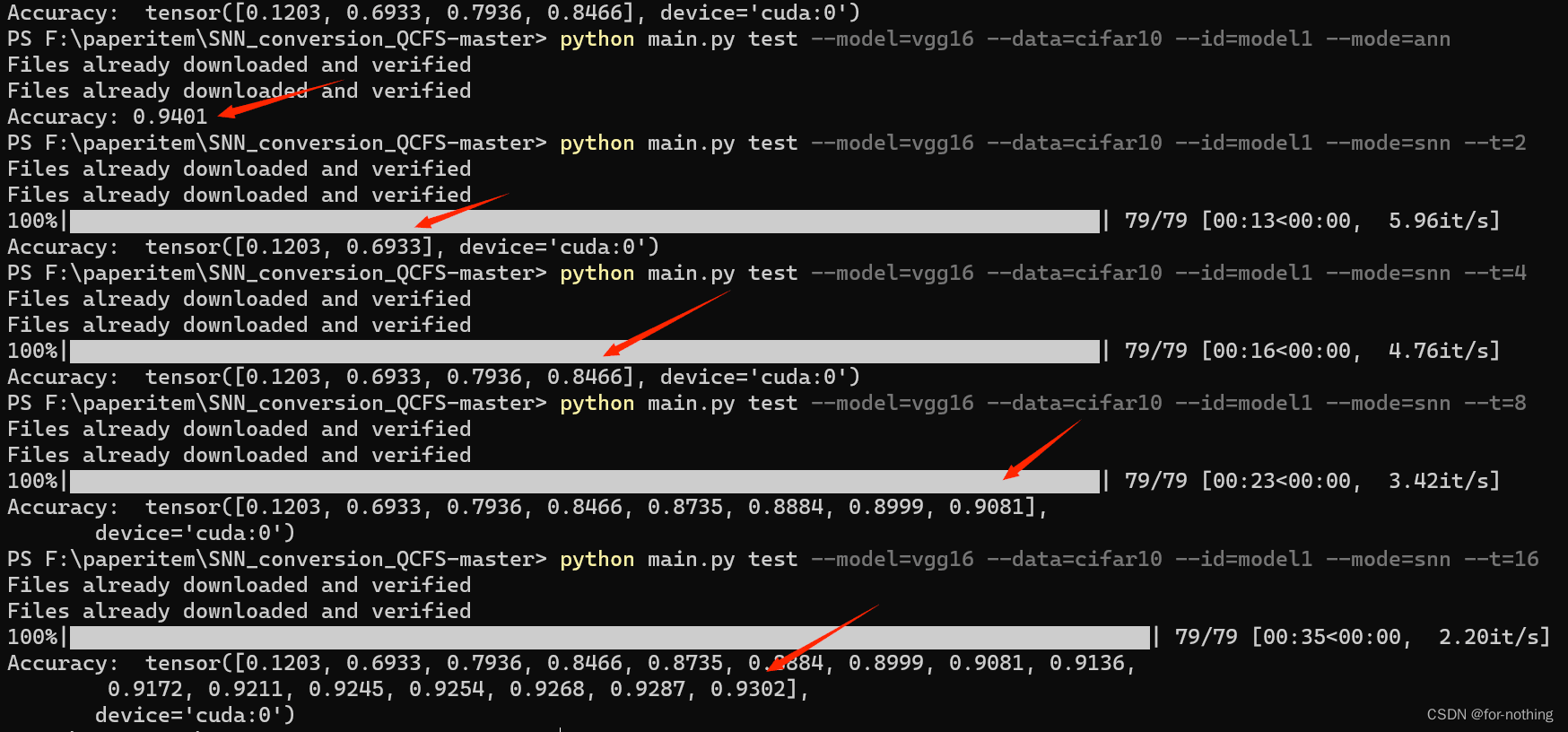
可以看到，随着T的增加，SNN的准确度越来越接近ANN的准确度，但是运行时间也随之增加，尽管如此，已经可以在较短的时间步长内达到十分优秀的准确率。

Abstract

为了解决传统的ANN-SNN转换中存在的时间步长过长会影响推理时间，而过短会导致性能倒退的问题，这篇论文从理论上分析了ANN-SNN转换中的误差，并提出了clip-floor-shift 激活函数用于ANN的训练，使得ANN-SNN的期望转换误差为0，从而得到高精度低延迟的脉冲神经网络。（是第一次高精度低延迟ANN-SNN转换的探索）

1.Introduction

目前ANN-SNN转换得到的SNN在大规模数据集上性能已经可以和ANN相当，相比于原始的ANN,转换得到的SNN速度快，功耗低更加实用。
在转换过程中SNN的时间步长T取得越大，得到的结果就越接近原始的ANN，然而这会导致巨大的运算量，从而阻碍SNN的实际应用。若是SNN的时间步长T取得过小，会使得产生的剩余势能$\frac{V^l(t)-V^l(0)}{T}$无法忽视，影响模型的精度。

创新之处：目前现有的文章都需要几十到几百的时间步长,而这篇论文中的方案将其缩短到了更少的时间步长（eg.4个时间步长）。
主要贡献：

• 将误差分为clipping error、quantization error、unevenness error
• 提出了用clip-floor-shift激活函数代替ANN中的Relu激活函数
• 在CIRAR-10,CIFAR-100以及ImageNet数据集上进行了测试，所提出的方法在更小的步长上超过了目前最先进的精度。

2.Preliminaries

2.1 ANN中的神经元模型：

$${\mathbf{\alpha }}^l=h({\mathbf{W}}^l{\mathbf{\alpha }}^{l-1})$$
其中${\alpha }^l$为第$l$层的输出，$W^l$是$l$和$l-1$层之间的权重矩阵，$h$ 是Relu激活函数

2.2 SNN中的神经元模型：

由Integrate-and-Fire（IF）模型：
$${\mathbf{m}}^l(t)={\mathbf{v}}^l(t-1)+{\mathbf{W}}^l{\mathbf{x}}^{l-1}(t)$$$${\mathbf{s}}^l(t)=H({\mathbf{m}}^l(t)-{\mathbf{\theta }}^l)$$$${\mathbf{v}}^l(t)={\mathbf{m}}^l(t)-{\mathbf{s}}^l(t){\theta }^l$$$${\mathbf{x}}^l(t)={\mathbf{s}}^l(t){\theta }^l$$
其中$m^l(t)$为t时刻脉冲产生前的电位，$v^l(t)$为t时刻脉冲产生后的电位，${\mathbf{\theta }}^l$是点火阈值${\theta }^l$的向量，H(*)是阶跃函数，${\mathbf{x}}^{l-1}(t)$是l-1层向l层的输入

2.3 ANN-SNN转换

由2.2节四个式子推导得到
$${\mathbf{v}}^l(t)-{\mathbf{v}}^l(t-1)={\mathbf{W}}^l{\mathbf{x}}^{l-1}(t)-{\mathbf{s}}^l(t){\theta }^l$$
同除时间步长T（time step），并累加0-T时间得到：
$$\frac{{\mathbf{v}}^l(T)-{\mathbf{v}}^l(0)}{T}=\frac{{\mathbf{W}}^l{\sum }_{i=1}^T{\mathbf{x}}^{l-1}(t)}{T}-\frac{{\sum }_{i=1}^T{\mathbf{s}}^l(i){\theta }^l}{T}$$
令${\varphi }^{l-1}(T)=\frac{{\sum }_{i=1}^T{\mathbf{x}}^{l-1}(t)}{T}$
有：
$${\varphi }^l(T)={\mathbf{W}}^l{\varphi }^{l-1}(T)-\frac{{\mathbf{v}}^l(T)-{\mathbf{v}}^l(0)}{T}$$
当令T足够大时该等式就几乎等同于2.1节中ANN的等式，即此时的SNN公式和ANN公式几乎相等，此时可以进行ANN-SNN的转化。
由于需要较大的T的限制条件，而较大的T会导致运算时间的增加，于是便产生了需要优化的问题：该如何减少T带来的影响。

3.Conversion error analysis

假设ANN和SNN中T时刻来自l-1层的输入相同，即${\mathbf{\alpha }}^{l-1}={\varphi }^{l-1}(T)$
令${\mathbf{z}}^l={\mathbf{W}}^l{\varphi }^{l-1}(T)={\mathbf{W}}^l{\mathbf{\alpha }}^{l-1}$
误差公式：
$${\mathbf{Err}}^l={\varphi }^l(T)-{\mathbf{\alpha }}^l={\mathbf{z}}^l-\frac{{\mathbf{v}}^l(T)-{\mathbf{v}}^l(0)}{T}-h({\mathbf{z}}^l)$$

3.1Clipping error

由于${\varphi }^l(T)=\frac{{\sum }_{i=1}^T{\mathbf{x}}^l(t)}{T}=\frac{{\sum }_{i=1}^T{\mathbf{s}}^l(t)}{T}{\theta }^l$在区间$[0,{\theta }^l]$
建立${\mathbf{\alpha }}^l$到${\varphi }^l(T)$的映射函数:
$${\varphi }^l(T)=clip(\frac{{\theta }^l}{T}\lfloor \frac{{\mathbf{\alpha }}^{l}T}{{\lambda }^l}\rfloor ,0,{\theta }^l)$$
clip函数表示当x < a 时结果为a，x > b时结果为b,b<=x<=b时结果为x.
考虑到99.9%的${\mathbf{\alpha }}^l$在区间$[0，\frac{{\mathbf{\alpha }}_{max}^l}{3}]$里，可以根据这个设置${\lambda }^l$
如下图(a),可以看出在${\mathbf{z}}^l>{\lambda }^l$的时候,全部被映射为${\theta }^l$,由此产生的误差即是Clipping error.

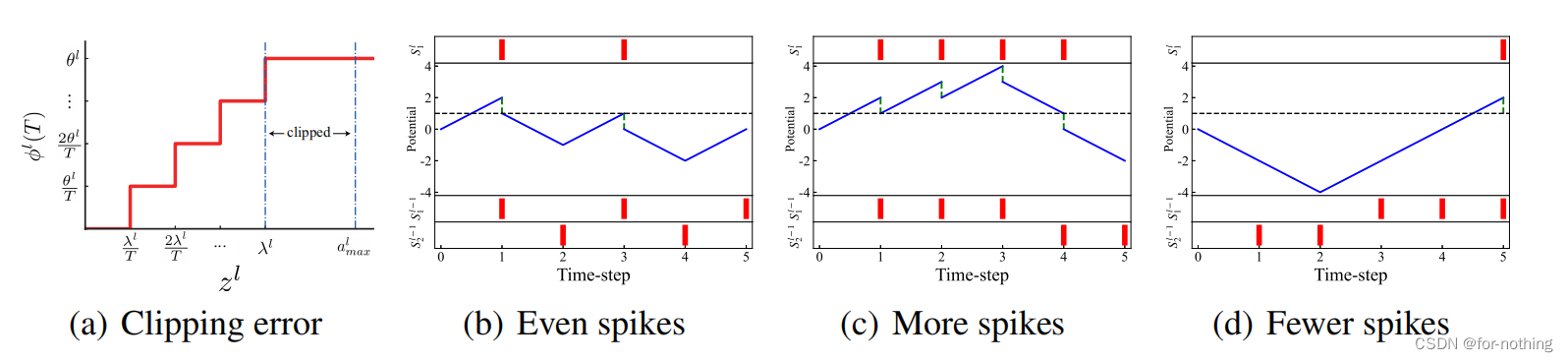
3.2Quantization error(flooring error)

由连续值映射到离散值不可避免的存在一些量化误差，比如在ANN中区间$[\frac{{\lambda }^l}{T},\frac{2{\lambda }^l}{T})$的${\mathbf{\alpha }}^l$全部被映射成了SNN中${\varphi }^l(T)$的$\frac{{\theta }^l}{T}$

3.3Unevenness error

不均匀误差是由于输入脉冲的不均匀造成的。
如上图（b）~（d）,最上方一栏是输出的脉冲，下方两栏是输入的脉冲。虽然脉冲数量相同，但是由于脉冲到达的时间不一样，所以产生的输出也不同，可能会产生比预期更多或更少的输出。
当${\mathbf{v}}^l(T)$在$[0,{\theta }^l]$的时候不均匀误差就会退化为量化误差，由于0<$\frac{v_i^l(t)}{{\theta }^l}$<1,此时：
$${\varphi }^l(T)={\mathbf{W}}^l{\varphi }^{l-1}(T)-\frac{{\mathbf{v}}^l(T)-{\mathbf{v}}^l(0)}{T}=\frac{{\theta }^l}{T}\frac{z^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}-\frac{{\theta }^l}{T}\frac{{\mathbf{v}}^l(t)}{{\theta }^l}\approx {\theta }^{l}clip(\frac{1}{T}\lfloor \frac{{\mathbf{z}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)$$
带入${\mathbf{Err}}^l$得：
${\widetilde{\mathbf{Err}}}^l={\theta }^{l}clip(\frac{1}{T}\lfloor \frac{{\mathbf{z}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)-h({\mathbf{z}}^l)\approx {\mathbf{Err}}^l$

4.Optimal ANN-SNN conversion

4.1Quantization clip-floor activation function

当ANN使用如下clip-floor激活函数的时候：
$${\mathbf{\alpha }}^l=\overline{h}(z^l)={\lambda }^{l}clip(\frac{1}{L}\lfloor \frac{z^{l}L}{{\lambda }^l}\rfloor ,0,1)$$
有定理1:
当$T=L,{\theta }^l={\lambda }^l,v(0)=0$的时候有$\widetilde{Err}={\varphi }^l(T)-{\mathbf{\alpha }}^l=0$
证明：
$${\mathbf{Err}}^l={\varphi }^l(T)-{\mathbf{\alpha }}^l={\theta }^{l}clip(\frac{1}{T}\lfloor \frac{{\mathbf{z}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)-{\lambda }^{l}clip(\frac{1}{L}\lfloor \frac{z^{l}L}{{\lambda }^l}\rfloor ,0,1)=0$$
然而实际应用中不能保证T=L,4.2节将介绍如何扩展到T不等于L的时候也使得期望为0

4.2Quantization clip-floor-shift activation function

当ANN使用如下clip-floor-shift激活函数的时候：
$${\mathbf{\alpha }}^l=\hat{h}(z^l)={\lambda }^{l}clip(\frac{1}{L}\lfloor \frac{z^{l}L}{{\lambda }^l}+\phi \rfloor ,0,1)$$
有定理2:
当${\theta }^l={\lambda }^l,{\mathbf{v}}^l(0)={\theta }^l\phi$的时候,对任意的T,L有$E_z(\widetilde{Err}){|}_{\phi =\frac{1}{2}}=0$：
证明：
引理1：设$x\in [0,\theta ]$以$p_t$的概率均匀分布在每个$[m_t,m_{t+1}]$的区间内，其中$m_0=0,m_{T+1}=\theta ,m_t=\frac{(t-1)\theta }{T},t=1,2,...,T,p_0=p_T$。
可以证明 $E_x(x-\frac{\theta }{T}\lfloor \frac{Tx}{\theta }+\frac{1}{2}\rfloor )=0$ （直接通过积分直接证明即可，详见论文）
（正是由于这个引理默认x均匀分布，而实际并非均匀分布，所以最后即使L=T，ANN与SNN的精度仍然存在差异）

由于$E_z(\widetilde{Err}){|}_{\phi =\frac{1}{2}}=E_z({\theta }^{l}clip(\frac{1}{T}\lfloor \frac{{\mathbf{z}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)-{\lambda }^{l}clip(\frac{1}{L}\lfloor \frac{z^{l}L}{{\lambda }^l}+\phi \rfloor ,0,1))$
对每个$z_i$有:
$$\begin{array}{rl}{E}_{z_i}(\widetilde{Err}){|}_{\phi =\frac{1}{2}}& =E_{z_i}(\frac{{\theta }^l}{T}clip(\lfloor \frac{{{\mathbf{z}}_{\mathbf{i}}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)-\frac{{\lambda }^l}{T}clip(\lfloor \frac{{z_i}^{l}L}{{\lambda }^l}+{\phi }_i\rfloor ,0,1))\\ & =E_{z_i}(\frac{{\theta }^l}{T}clip(\lfloor \frac{{{\mathbf{z}}_{\mathbf{i}}}^{l}T+{\mathbf{v}}^l(0)}{{\theta }^l}\rfloor ,0,1)-z_i^l)+E_{z_i}(z_i^l-\frac{{\lambda }^l}{T}clip(\lfloor \frac{{z_i}^{l}L}{{\lambda }^l}+{\phi }_i\rfloor ,0,1))\\ & =0+0(由引理1)\\ & =0\end{array}$$
这样便有了对任意T,L的都可以使得转换误差的期望为0的激活函数以及转换方法

4.3 Algorithm for training quantization clip-floor-shift activation function

使用随机梯度下降法以转换误差为代价函数，学习${\mathbf{W}}^l$(由z^l得到)和${\lambda }^l$参数
其中
$$\frac{\partial {\hat{h}}_i({\mathbf{z}}^l)}{\partial z_i^l}=\{\begin{array}{rl}1& if-\frac{{\lambda }^l}{2L}<z_i^l<{\lambda }^l-\frac{{\lambda }^l}{2L}\\ 0& otherwise\end{array}$$
$$\frac{\partial {\hat{h}}_i({\mathbf{z}}^l)}{\partial {\lambda }_i^l}=\{\begin{array}{rl}\frac{1}{2L}& if-\frac{{\lambda }^l}{2L}<z_i^l<{\lambda }^l-\frac{{\lambda }^l}{2L}\\ -\frac{z_i^l}{({\lambda }^l{)}^2}& otherwise\end{array}$$

5.Related work

由于该内容较少且不是论文重点，这里便不详细进行阐述。

6.Experiments

这篇论文在CIFAR-10、CIFAR-100以及ImageNet数据集上进行了实验，验证了该方法的有效性，并且与世界最先进的方法进行了比较。

6.1 比较ANN使用Relu、clip-floor与clip-floor-shift的表现

其中顶端虚线是使用Relu作为激活函数的ANN的准确率，绿色和蓝色的实线分别是使用clip-floor和clip-floor-shift作为ANN的准确率随量化间距L变化的函数函数。可以看出在L>4时都已经非常接近甚至超越Relu的准确率，由此可见使用该函数不会对性能造成较大影响。

6.2和世界最先进的方法比较

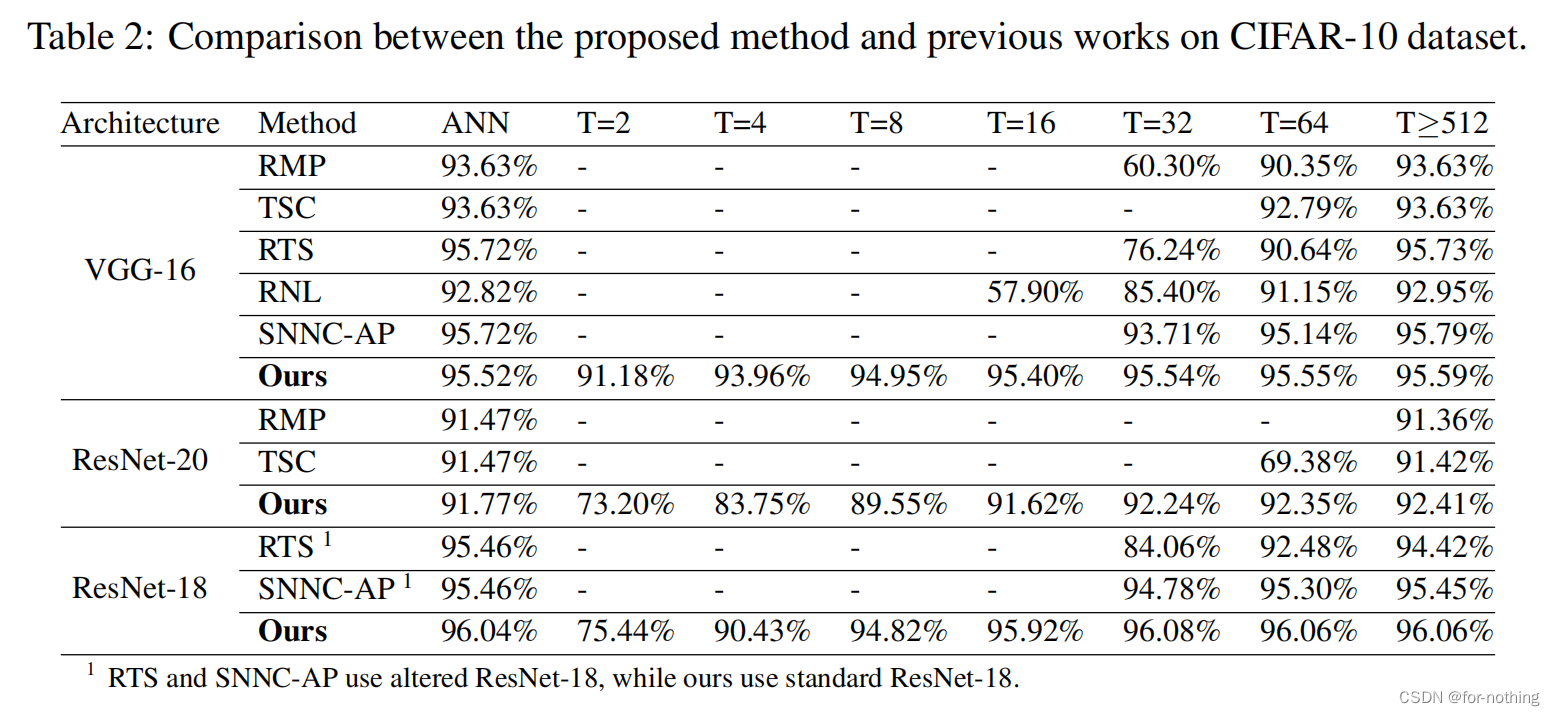
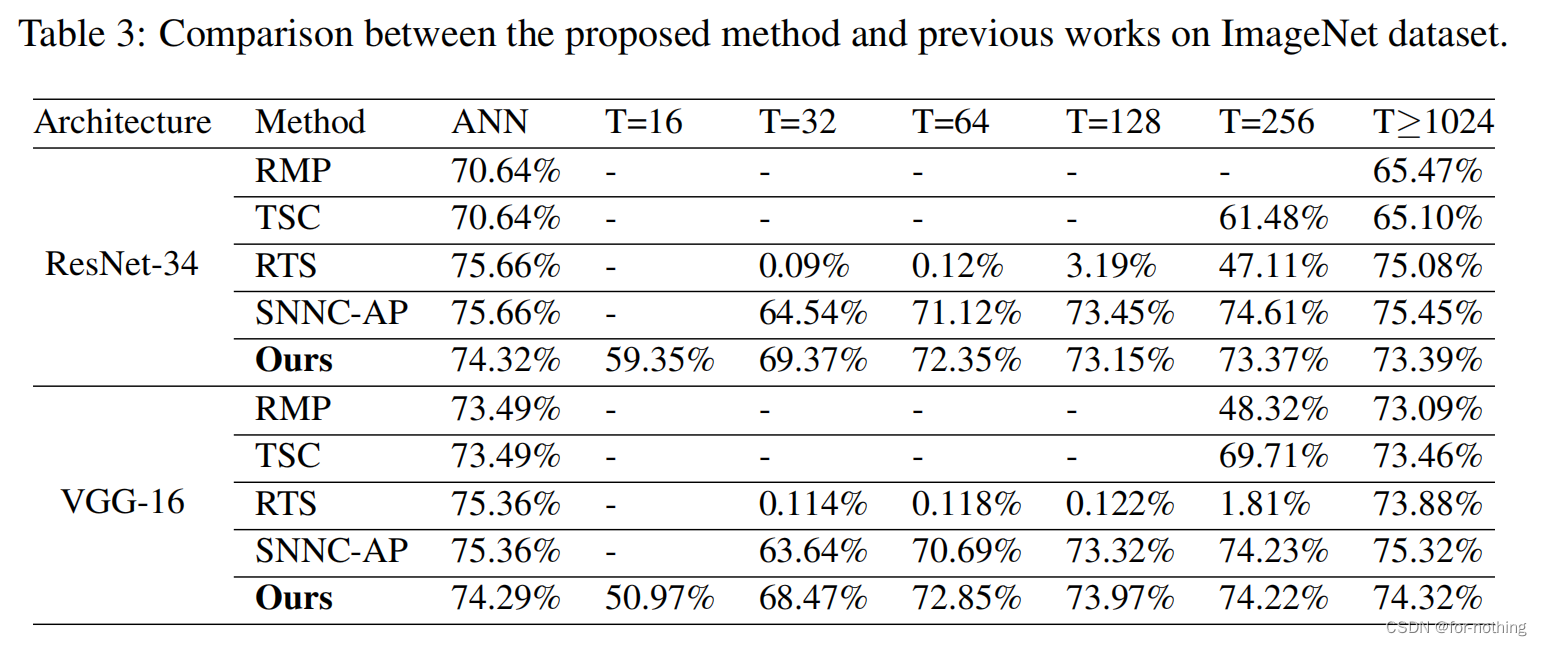
AN那一列指的是是ANN各个算法的ANN的准确率，后面的每一列指的是采用不同的时间步长下ANN转换为SNN之后的准确率，可以看出这篇论文的方法相比于其他方法可以在更短的时间内快速完成高准确率的转换。

6.3比较ANN转换得到的SNN使用clip-floor与clip-floor-shift的表现

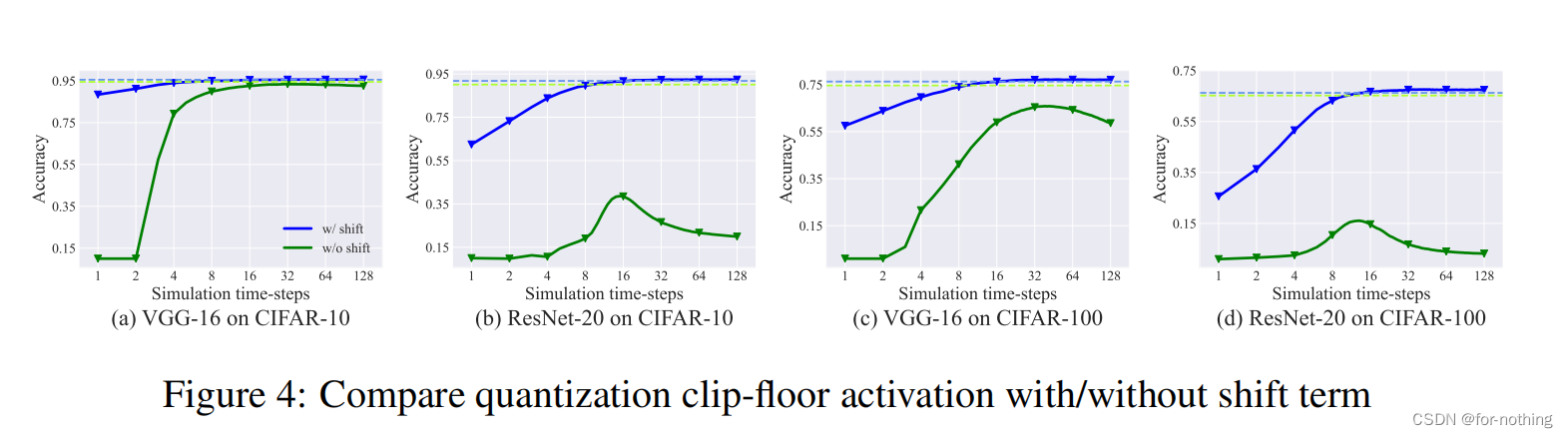
其中顶端虚线是该方法使用的ANN转换得到SNN的最高准确率，绿色和蓝色的实线分别是使用clip-floor和clip-floor-shift作为ANN转换得到的SNN的准确率随时间步长T变化的函数函数（量化步长L取固定值4）。
可以看出随着T的增大clip-floor-shift的性能逐渐接近于最优性能，符合clip-floor-shift期望误差为0的理论。

6.4比较量化步长L对实验结果的影响

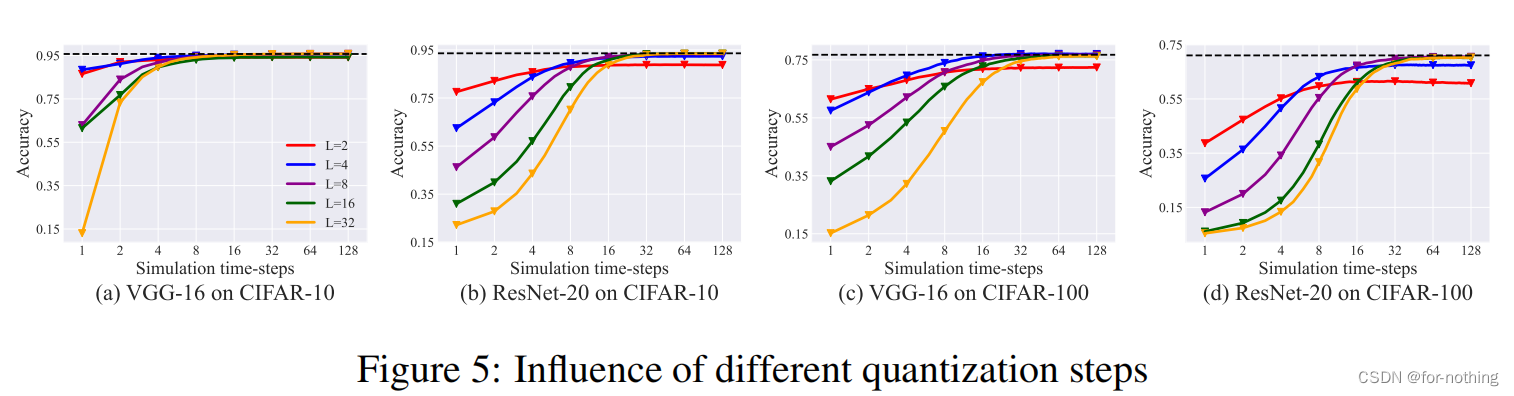
可以看出如果量化步长L取得太小，虽然可以使用较短的时间步长T取得较高的转化结果，但是继续增加T也难以达到的与最优准确率接近的结果。如果量化步长L取得太大，则需要较大的时间步长T才可以使其准确率接近最优准确率。所以综合考虑要取一个适中的L值，一般取4或者8。

7.Discussion and conclusion

优点：这篇论文提出了clip-floor-shift 激活函数代替Relu用于ANN的训练，这样训练出来的ANN可以在快速转换为SNN的同时保持有较高的准确率。这样转换得到SNN相比原先的ANN具有相当的性能却只需要更少的计算成本。

值得深究之处：1.由于均匀误差的存在使得ANN与SNN的准确率始终存在差距。2.当时间步长为1的时候很难实现高性能转换。

此外，论文附录中的证明相关内容已经结合在上述部分中进行了介绍，附录中的其余实验结果这里详细阐述了。

最后

以上就是秀丽白云为你收集整理的Optimal ANN-SNN Conversion for High-accuracy and Ultra-low-latency Spiking Neural Networks 阅读总结运行结果演示Abstract1.Introduction2.Preliminaries3.Conversion error analysis4.Optimal ANN-SNN conversion5.Related work6.Experiments7.Discussion and conclusion的全部内容，希望文章能够帮你解决Optimal ANN-SNN Conversion for High-accuracy and Ultra-low-latency Spiking Neural Networks 阅读总结运行结果演示Abstract1.Introduction2.Preliminaries3.Conversion error analysis4.Optimal ANN-SNN conversion5.Related work6.Experiments7.Discussion and conclusion所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。