作者丨王维埙
学校丨天津大学硕士生
研究方向丨DRL & MAS
以彼之道还施彼身

■ 论文 | Maintaining Cooperation in Complex Social Dilemmas Using Deep Reinforcement Learning
■ 链接 | https://www.paperweekly.site/papers/1558
为什么要叫做以彼之道还施彼身,是因为这篇文章借鉴了 TFT 的思想,扩展成 amTFT。而我对 TFT 的第一反应就是姑苏慕容的以彼之道还施彼身。
这篇文章是 Facebook AI Research 投在今年 ICLR 上面的文章。不算很好,但是想要解决的问题还是很有意义的,所以大家可以辨证地看这篇文章,希望能让各位有所收获。
核心问题
1. 研究问题:在 complex social dilemmas 中如何设计出既能考虑 social welfare,又能确保自己 payoff 的 agent。
2. 假设条件:能够观察到对手的 action,能够事先知道环境。
3. 主要想法:如果想要最大化 social welfare,那么就是在对手能够合作的时候与对手合作。要确保自己的 payoff,就是在对手背叛的时候,自己也背叛,确保自己不会被对手利用。
4. 解决方案:
事先训练出 fully cooperative policy 与 safe policy(defection)的策略,同时获得双方都合作/竞争时的 Q 与 V;
然后通过对比对手当前 action 的 Q(合作)的值与对手当前 action 的 Q(合作)的值,如果当前 action 的 Q 值更高,就说明对手采用背叛的action;
累积对手背叛的程度,在一定阈值后,采用 K 次背叛的策略(K 的次数类似惩罚,采用 V 值进行计算),然后再切换成合作的策略,再次循环。
Background
关于 social dilemma,简单地说就是 agent 们相互合作能够得到比较高的 payoff,同时 total payoff 是最高的,但是不论在什么情况下,采用 selfish 的 action 能够比采用合作的 action 获得更高的 payoff,所以 agent 为了自己的 payoff 有动机采用 selfish 的 action。
但是双方都采用 selfish 的 action 时,payoff 反而比都合作时候的 payoff 低,同时 total payoff 也比较低。
通常对于 social dilemma 的研究环境,我们都采用是 repeat game,就是固定一个矩阵的 game,然后不停地玩这个 game。
在 Deepmind 的 Multi-agent Reinforcement Learning in Sequential Social Dilemmas 中,将 social dilemma 扩展到了 sequential 下,因为环境更复杂了也带来更多的挑战。
比如 defection 和 cooperative 是体现在一些列 actions 中,我们很难通过 actions 来判断是合作还是竞争,同时传统的 ISD 直接的方法不能直接扩展到 SSD 下面。
那么我们自然会想到使用 DRL。在复杂的 mas 环境中,我们通常使用 DRL+self-play 来训练 agent,用简单地话说,self-play 就是不断重复模拟 game,在模拟中控制所有的 agent,并不断地 improving 这些 agent 的策略,并最终获得训练好的策略,在面对新的,未知的对手时,采用训练好的 policy 来应对。
本文思路
但是在 SSD 中,我们并不能简单地使用 DRL+self-play 来训练 agent,主要原因是一个一直采用 cooperative policy 的 agent 容易被对手利用,一个一直采用 defection policy 的 agent 最终只能与一个理智的对手达成 social dilemma。
因此我们应该设计出一种算法,让 agent 能够根据对手的行为来调整采用 cooperative 还是 defection。
一个经典的做法叫做 Tit For Tat(TFT),TFT 就是在第一局采用合作,然后在以后的局面中采用对手上一局采用的 action。
说来简单,但是 TFT 是一个非常强大的算法,能够与能合作的对手合作,避免被对手利用,同时一旦对手能够选择合作,就会选择合作,并有希望一直保持合作。
从描述中,我们就能很直观地发现 TFT 并不能直接用在 SSD 的情况下,主要的原因是环境已经从一个矩阵,变成一个需要做序列决策的环境了。
虽然 TFT 不能直接用,但是我们可以利用 TFT 的思想来构造一个与 DRL 相互结合的算法,也就是这里的算法:APPROXIMATE MARKOV TFT(amTFT)。
TFT 能够直接用上一局对手的 action 来选择自己这句的 action 的主要原因就是,在传统的矩阵形式的 game 中,action,reward,defection,cooperative 这几个其实可以理解为等价的,一者确定之后,其他就确定了。
比如我选择 defection 的 action,那么它的 reward 信息就大致确定了(因为还与对手的 action 相关),所以在这里我不严谨地说:选择 action,本质上也就是在利用 reward 的信息。
那么就很直观,在矩阵下面我利用 reward 的信息,在一个序列的决策中,我们就可以利用 Q 或者 V 的信息,amTFT 就是利用 Q 与 V 的信息。
具体做法
首先,我们采用 selfish 的方式,每个 agent 都是最大化自己的 reward 的方式,来训练自己的 policy,我们可以得到 agent ![]() 的策略 , 相应的 Q function approximations
的策略 , 相应的 Q function approximations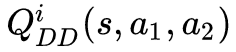 。
。
然后我们在采用 fully cooperation 的方式,agent 目标是最大化 total payoff 的方式来训练策略,同样我们可以得到 agent 的策略![]() , 相应的Q function approximations
, 相应的Q function approximations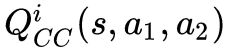 。
。
那么如果我们要衡量在当前 state s 下,我们合作时(假设我们是 agent1 ,对手是 agent2),对手当前 action 是否是合作的?
我们可以使用双方都合作的时的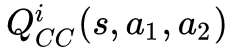 ,假设对手采用合作策略
,假设对手采用合作策略![]() 时,和当前采用 action 的 Q 的差值,如果当前 action 的 Q 值,则说明对手采用了竞争的 action,即为下式:
时,和当前采用 action 的 Q 的差值,如果当前 action 的 Q 值,则说明对手采用了竞争的 action,即为下式:
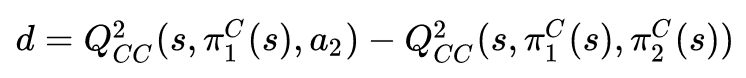
当 d 大于 0 时,我们觉得对手是采用竞争的策略,那么我们可以变化自己的策略为竞争的策略。
在这里 amTFT 的实际做法并不是像 TFT 那样,不停地按照对手的 action 来调整自己的 action,而是变化为 defect 之后,保持 defect k step,然后调整为 cooperation,再次观察对手的合作程度。
这里就带来两个问题,一个问题是:一次 d 其实并不准确,容易有很大的误差。另外的问题是:k step 的 k 该如何决定?
第一个问题其实比较好解决,我们可以不停的累积 d,直到 d 的累积和超过一个阈值,我们认为对手是 defect,然后再变换为 defect 的策略。这样通过累积的方法,更加容忍 d 计算上可能的问题,但是实际上也带来了一定的延迟性。
第二个问题其实也蛮重要的,因为如果采用固定的 k,容易被对手考虑全局,在某个 s 下来利用这个性质。所以这里采用类似惩罚的思想,使用第一个问题中累积的 d,来计算我应该惩罚对手多少局,它才会把这几次背叛获得更多的 payoff 损失掉:
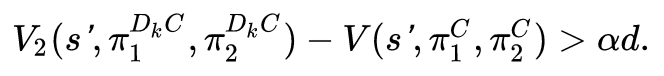
其中 α 为超参数,大于 1,![]() 代表采用 D k step 后切换成 C。所以这里其实是定义了一个下界。 整体的算法如下所示:
代表采用 D k step 后切换成 C。所以这里其实是定义了一个下界。 整体的算法如下所示:

实验
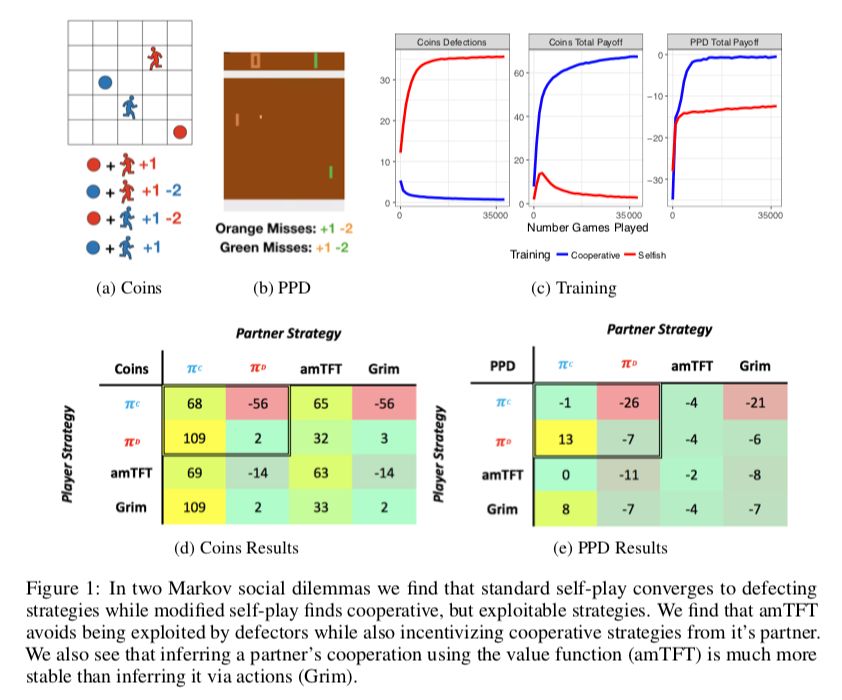
在这里做了两个实验环境:
coin game:在一个 5x5 的格子世界中,有两个不同颜色的 agent,也有两个不同颜色的 coin,agent 不论收集到什么颜色的 coin,agent 都会得到 +1 的 reward,但是如果 agent 收集到了另外颜色的 coin,对应颜色的 agent 会得到 -2 的 reward。
一般情况下,selfish 的 agent 就算不论什么颜色都收集,合作的 agent 都只会收集自己的颜色的 coin。
Pong Player’s Dilemma (PPD):就是将 Pong 扩张成 SSD 的情况,赢球的 agent 获得 +1 的 reward,输球 的agent 获得 -2 的 reward。所以 selfish 就是努力自己得分,合作就是双方尽力不得分,在中间传球。
在这两个环境中,amTFT 达到了我们的目的:与合作的合作,与竞争的竞争,相互直接合作。
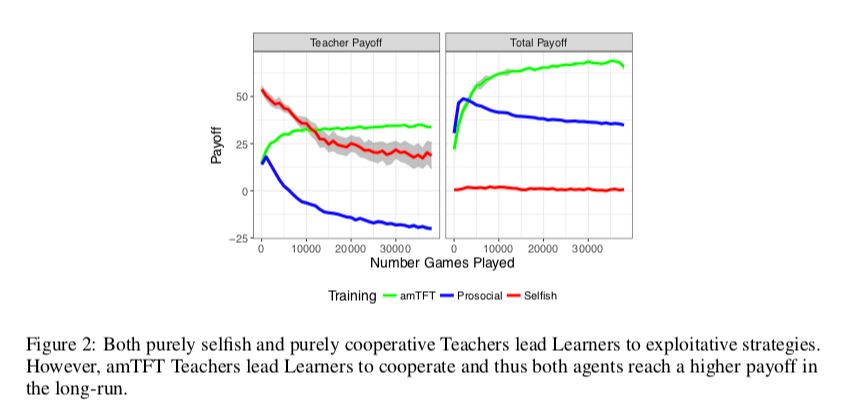
然后我们研究如果固定一个 agent 的策略,另外一个 agent 用 selfish 的角度,从头开始学会怎么样(结果如上图)。
这里采用的固定的 agent 的策略为:合作,竞争,amTFT。面对合作/竞争的 agent 时,selfish 学到利用。面对 amTFT,selfish 最终学到合作。
小无相功

■ 论文 | RL^2: Fast Reinforcement Learning via Slow Reinforcement Learning
■ 链接 | https://www.paperweekly.site/papers/1560
小无相功可以模拟各种武功,只要你学了,各种武功皆数模仿,就向对 reinforcement learning 做 meta-learning,学会了 reinforcement learning,还有什么学不会。
核心问题
1. 研究问题:如何对reinforcement learning进行learning,也就是meta-learning。
2. 假设条件:知道想要解决的问题的模型是什么样(能够构造一大组(分布)MDP)。
3. 主要想法:如果在一大组 MDP 中学习到的 agent,在面对未知(新的)MDP 时,能有不错的效果,说明 agent 已经学到这类 MDP 的性质,也就是 prior。
4. 解决方案:用 RNN 来学习,用一大组 MDP 训练出 RNN 的权重(视为 meta-learning),然后面对新的 MDP 时,用不断产生的 input 来调整 hidden state,将不断变化的 hidden state 是为当前 MDP 的 reinforcement learning。
思路
通常我们都是针对具体类型的问题设计相应的算法,因为是针对具体类型的设计,所以这样的算法必然性能等方面会比较好,但是也因为是对于具体类型设计的,所以必然会有更多的局限性,对于别的类型可能并不适用。
因此我们会想:能不能有万能算法能够针对不同类型的问题,学习出相应的类型,然后自己根据问题类型,来学习设计出算法?
deep learning 已经具有一定提取特征的能力了,所以懒惰的我们肯定会想如果 agent 能够根据问题自己调整出网络结构那该多好。这有点跑题了,但这也就是这篇文章,或者 meta-learning 所希望有的能力:learning to learn。
不同类型的问题和不同类型的算法有不同的学习范式。对于 Reinforcement Learning 当然最重要的一点是:MDP,因为 RL 的目的是针对特定的 MDP 学习出最优或者不错的 policy。
那么我们希望能够让 agent 学习到 RL 的能力,那其实就是希望能够学习到在不同 MDP 中寻找最优 policy 或者不错 policy 的能力。
这其实有点大,或者说有点难,因为 MDP 的各个部分其实有很多的伸缩性,所以对 training 等方面是有很大的挑战的。
因此本文其实做了一个假设:我们事先知道要解决是什么问题,根据这个问题的类型,构造了一堆 MDP,然后在这堆 MDP 中学出 MDP 中的特性,并将其应用在这个问题上,说明我的 agent 已经学习到了这类 MDP 的性质。
具体做法
PRELIMINARIES
discrete-time finite-horizon discounted Markov decision process (MDP) .

RL^2
如果我们使用 RNN 来构造 agent,agent 的输入为:以前的 rewards,actions,termination flags 和 normal received observations。
同时 RNN 的 hidden state 并不在每次 episode 开始后重置,而是保留,然后使用标准的 RL 算法来 training 这个 agent,那么这个 agent 应该能 capacity to perform learning in its own hidden activations。
这个 agent 在 deployed 时,面对未知的 MDP 应该能够根据当前的信息来调整 hidden state,也就是学习到了 RL 的能力,这也正是本文被称之为 RL^2 的原因。
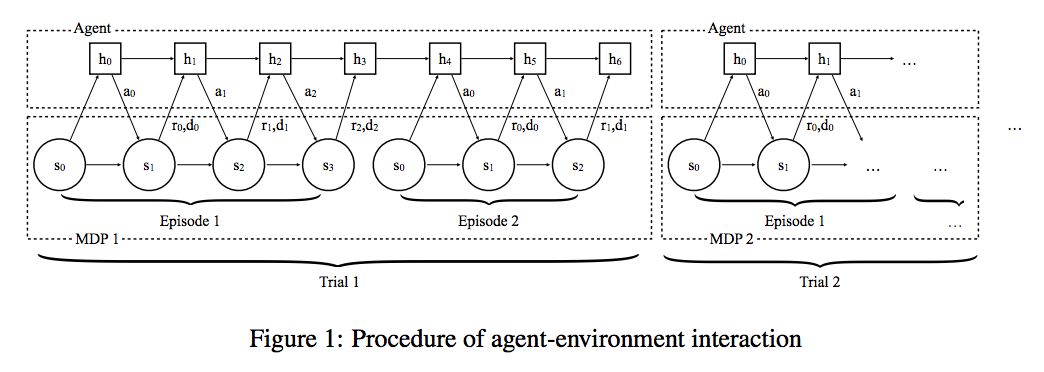
首先定义一个 MDPs 的知识,也就是在一大堆 MDP 中每个 MDP 被抽样的概率: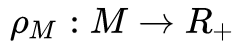 ,然后每次我们通过这个 M 来抽取MDP,抽取后将这个 MDP 固定 n 个 episode,比如上面的图就是固定了 2 个 episode,也就是 n=2 。然后再继续抽取新的 MDP,这样不断的学。
,然后每次我们通过这个 M 来抽取MDP,抽取后将这个 MDP 固定 n 个 episode,比如上面的图就是固定了 2 个 episode,也就是 n=2 。然后再继续抽取新的 MDP,这样不断的学。
这里的细节是:agent 会使用上一时刻的 reward![]() ,上一时刻的action
,上一时刻的action![]() ,上一时刻的termination flag
,上一时刻的termination flag![]() (从上图可知,我们时是固定了一个 MDP n episode,所以需要明显地知道结束)和当前的state
(从上图可知,我们时是固定了一个 MDP n episode,所以需要明显地知道结束)和当前的state![]() 做为agent的输入的。
做为agent的输入的。
另一个重点是:我们是最大化这 n 个 episode 的 expected total discounted reward,这其实等价于 minimizing the cumulative pseudo-regret。
同时因为我们每次都是抽去出的 MDP,所以 agent 并不知道面对的是哪一个 MDP,所以 agent 应该要能够利用历史上的 input 推测出这个 MDP 的信息,然后调整 policy,也就是 hidden state。
MULTI-ARMED BANDITS
就是经典的多臂赌博机,这里存在很多个臂,然后从这些臂里面抽取出一些臂做为一个赌博机来学习,每个臂被抽出的概率为 p_i ,所以是可以抽取多个赌博机,这就是上面说的 MDP 的 set,我们的目的是:maximize the total reward obtained over a fixed number of time steps。
这是个单状态的问题,但是也要平衡探索与利用,因为研究的比较多,同时有 rich theory,可以与一些有理论保证,渐进线形最优的 policy 做对比,If the learning is successful, the resulting policy should be able to perform competitively with the theoretically optimal algorithms.
这里与几个 policy 做了对比:
random
gittins index
UCB1
Thompson sampling (TS)
ε-greedy
greedy
同时,我们把所有的 true distribution 提供给上面需要的算法( RL^2 除外)。
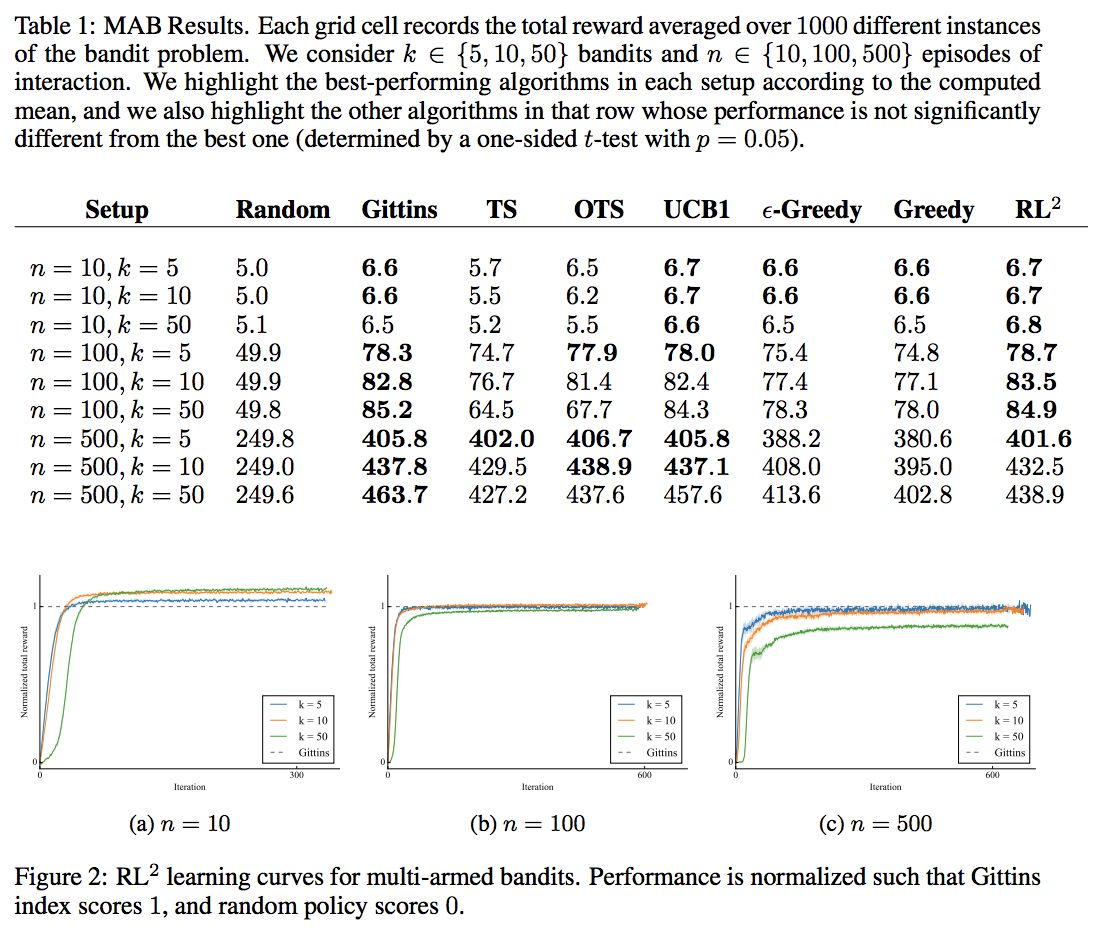
还是不错的,但是因为已有的算法 mostly designed to minimize asymptotic regret (rather than finite horizon regret), hence there tends to be a little bit of room to outperform them in the finite horizon settings.
另外发现说在 n=500,k=50 和 index 有一些差距,为了探索是不是学出来的 RL 不够好,就使用相同网络结构,然后用 index 来生成数据对网络做 SL,发现能学的和 index 差不多,说明 RL 学的还是有提升空间的。
TABULAR MDPS
多臂赌博机是一个单状态的,但是 RL 是针对 sequential decision making 的,所以这里就采用随机生成 tabular MDP 来做测试。
这里我们限制 state 空间为 10,action 空间为 5,rewards follow a Gaussian distribution with unit variance, and the mean parameters are sampled independently from Normal(1, 1) ,transitions are sampled from a flat Dirichlet distribution,然后 episode 的 horizon 为 T=10。
然后与下面比较:
random
PSRL
BEB
UCRL2
ε-greedy
-
greedy
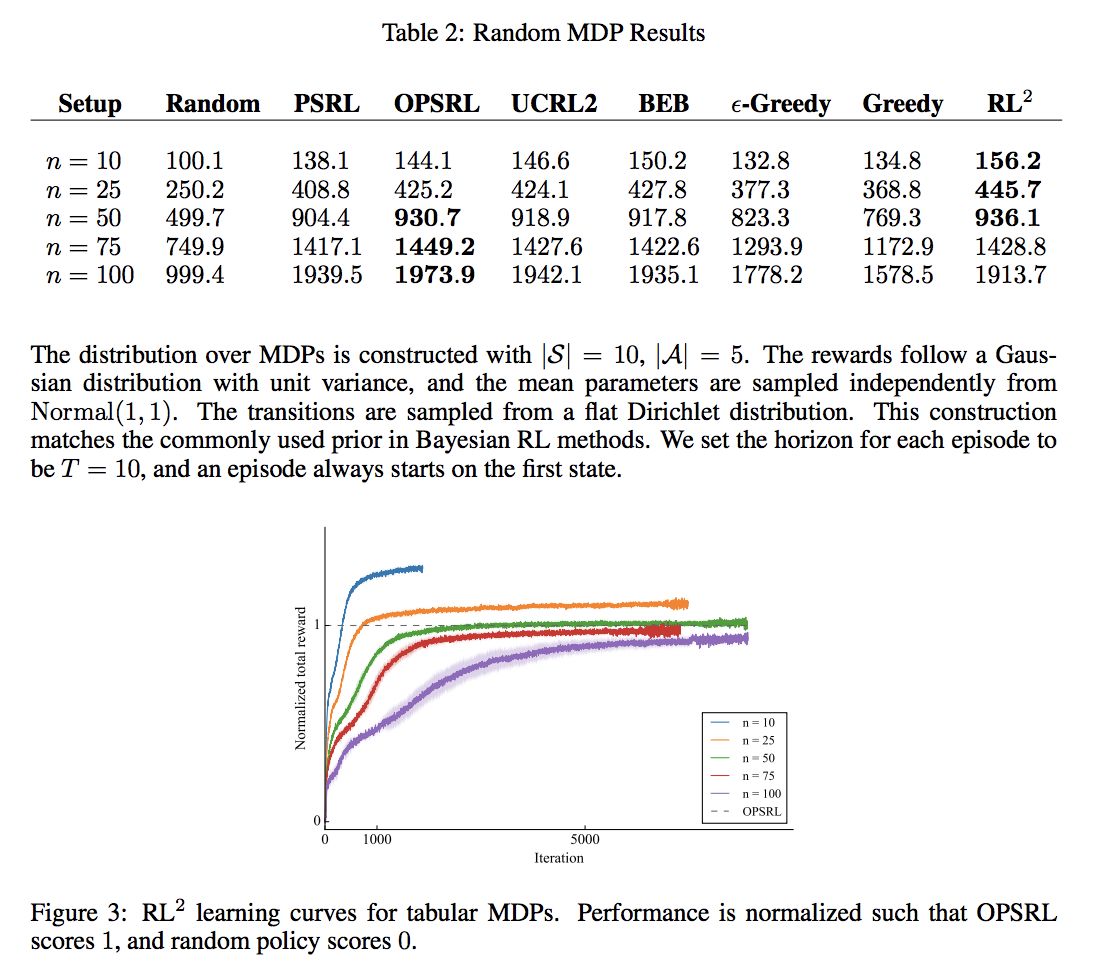
发现还是有一定效果的。
VISUAL NAVIGATION
每个 MDP 是随机产生的 maze,然后目标是也是随机的,但在一个 mdp 的不同 episode 下,maze 与终点时固定的。reward 和 cost 设置为:找到目标 reward+1,如果碰墙,cost 掉 -0.001,每个时间 step,cost 掉 -0.04。
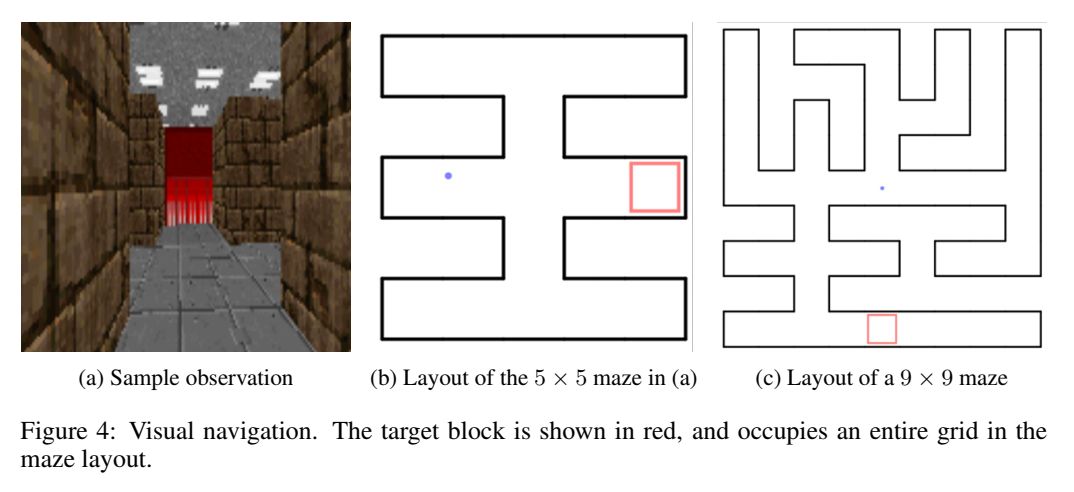
先在 5x5 的世界中做 training,n=2,horizon=250。然后 maze 是从 1000 个 configuration 中产生的。在 test 时做了以下工作:1. 在 9x9 与 5x5 里面看看效果如何;2. 将 agent 运行 5 个 episode 看看怎么样。
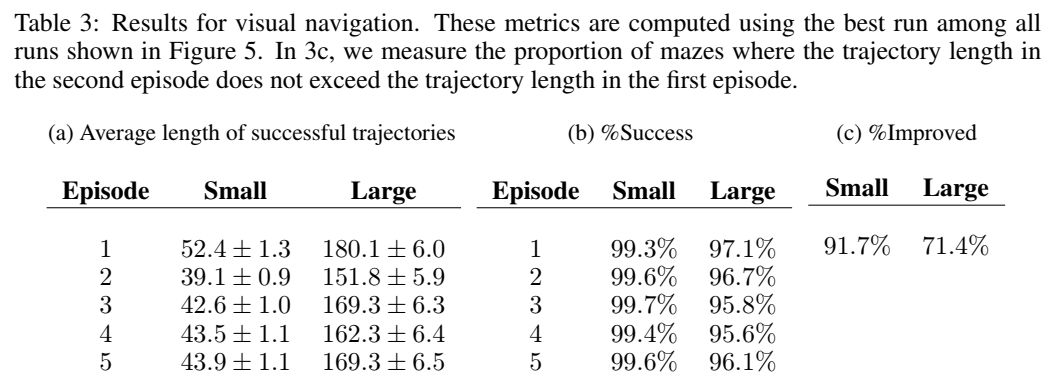
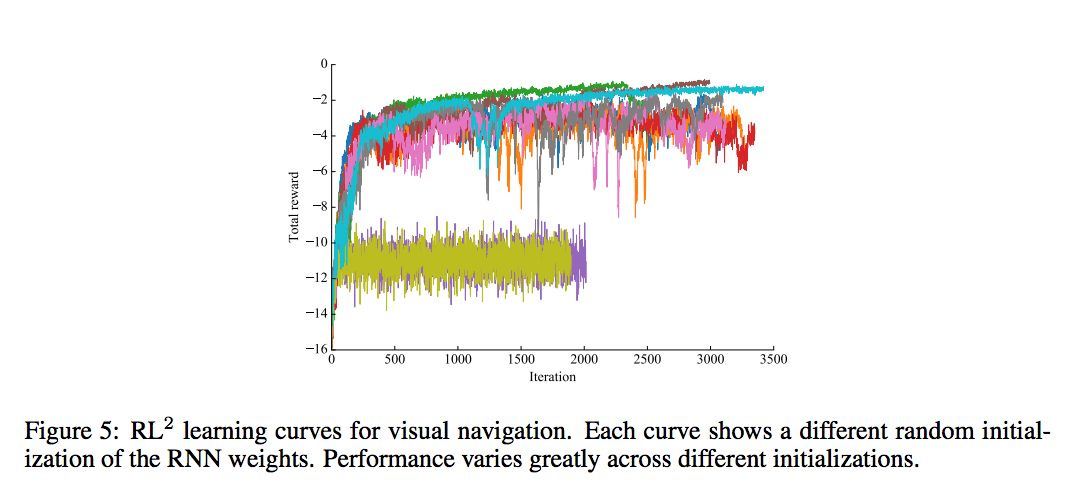
POLICY REPRESENTATION
输入 (s, a, r, d) ,通过函数 Φ (s, a, r, d) 做 embedded 后做为 RNN 的输入,RNN 的 cell 采用 GRU,然后在接一层全连接,再使用 softmax 做为激活函数,输入为每个 action 的概率。
另外这里说参数在每个 episode 开始的时候重置一部分的 hidden state,这样的目的其实是说开始和结束必然存在一些不一样,希望学到这部分不一样,但是实际实验并没有效果。
采用 off-the-shelf RL algorithm:rllab and TabulaRL,使用 first-order implementation of Trust Region Policy Optimization (TRPO),同时To reduce variance in the stochastic gradient estimation, we use a baseline which is also represented as an RNN using GRUs as building blocks. We optionally apply Generalized Advantage Estimation (GAE).
hidden activation: relu
all weights matrices use weight normalization without data-dependent initialization
hidden to hidden weight: orthogonal initializaion
other weight: Xavier initialization
bias: 0
the policy and the baseline uses separate neural networks with the same architecture until the final layer, where the number of outputs differ.
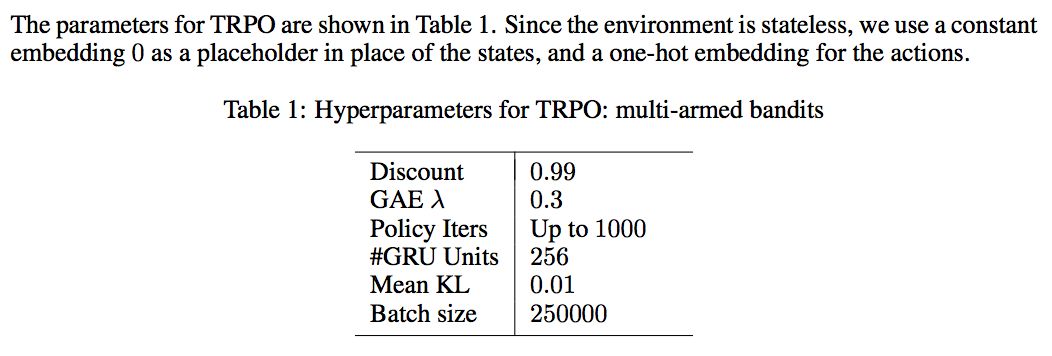
MULTI-ARMED BANDITS
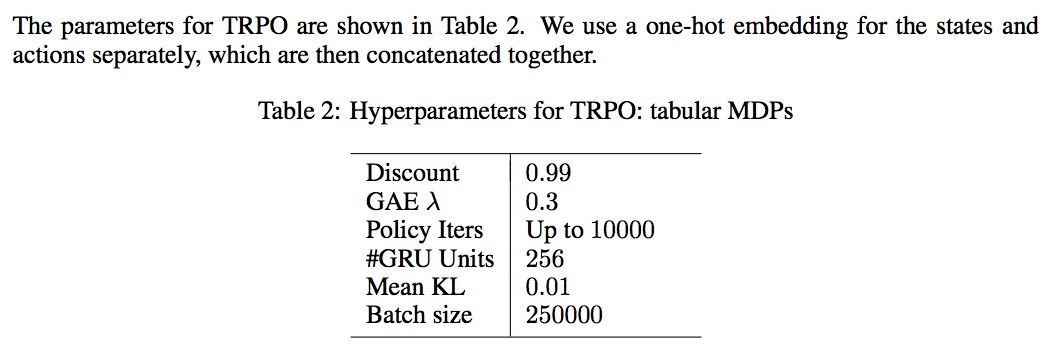
TABULAR MDPS
VISUAL NAVIGATION
40 x 30 RGB image, range [-1, 1]
2 层 Conv:16 个 filter, size 5 x 5, stride 2
将 action embedded 到 256-dimensional vector,然后与 2 的输出 flattened 后拼接
256 hidden dense

左右互搏:self-play

■ 论文 | Emergent Complexity via Multi-Agent Competition
■ 链接 | https://www.paperweekly.site/papers/861
这篇文章给我们的最大启发是,在实际工作中如何训练一个比较复杂的 agent。
实验效果蛮有趣的:
class="video_iframe" data-vidtype="2" allowfullscreen="" frameborder="0" data-ratio="1.7647058823529411" data-w="480" data-src="http://v.qq.com/iframe/player.html?vid=e05357faa7p&width=654&height=367.875&auto=0" style="display: block; width: 654px !important; height: 367.875px !important;" width="654" height="367.875" data-vh="367.875" data-vw="654" src="http://v.qq.com/iframe/player.html?vid=e05357faa7p&width=654&height=367.875&auto=0"/>
class="video_iframe" data-vidtype="2" allowfullscreen="" frameborder="0" data-ratio="1.7647058823529411" data-w="480" data-src="http://v.qq.com/iframe/player.html?vid=x05353s67kp&width=654&height=367.875&auto=0" style="display: none; width: 654px !important; height: 367.875px !important;" width="654" height="367.875" data-vh="367.875" data-vw="654" src="http://v.qq.com/iframe/player.html?vid=x05353s67kp&width=654&height=367.875&auto=0"/>
核心问题
1. 研究问题:在 MAS 环境下,如何稳定,有效地训练一个具有复杂能力的 agent。
2. 假设条件:普通的 multiagent 假设,没有中心式的 critic,independent training,不用知道对手的 action 和 policy。
3. 主要想法:利用 self-play 的思想,产生合适的对手。同时利用额外的 reward 来帮助学习 basic action。
4. 解决方案:设计 Exploration Curriculum,前期利用额外的 reward 来帮助学习基本 action,后期将这部分额外的 reward 衰减掉,让 agent 能够学习大宋真正希望学习的任务。使用 Opponent Sampling,避免对手一旦学的很好,使的自己的 agent 无法学习,无法收敛。
其实很多学科最终都是要实用,现在的 DRL 玩玩 Atari 的游戏还好,但是面对更难的游戏,比如星际二的时候,其实效果并不好,主要的原因是星际二的环境更复杂,我们需要学习出一个更复杂的 agent。
抽象地说环境的复杂性与学习出 skill 的复杂性是相关的,越复杂的环境就能学习出越复杂的 skill。但是我觉得复杂的话,有时候很难学,所以我们可能需要更多的工程上的努力。
不同的 single agent 的复杂性只与环境本身相关,比如你总不能让一个普通 pixel 的 pong 的 agent 学出正手,反手击球吧。
但是在 multiagent 的环境中,复杂性其实还与对手是相关的,比如围棋,规则很简单,但是你在和对手博弈的过程是十分复杂的。
围棋的新手与高手有很大的区别,如果你让你的 agent 一直与一个新手玩,这个 agent 可能最多就战胜这个新手,但是实际上不会很厉害。
如果你让你的 agent 一开始就和柯洁下,按照 RL 的学习方法,开始探索,然后慢慢学习,估计 agent 一盘都赢不了,最终什么都没有学到。
因此,如何在一个环境里面学习到更复杂的策略、如何有效地进行学习才是本文的目的。
Exploration Curriculum
这里假设环境都只在最后通过结果给予 agentreward(后面环境设置都是如此),那么必然就带来 reward 稀疏的问题。
一般的稀疏的 reward 的问题,通过随机探索可以得到一定缓解,但是如果需要一些基本 basic 的行为,然后再做操作的任务,可能随机探索就不是很好了。
比如一个经典的 HRL 的例子: 我们希望一个机器人移动到门边,然后推开门,只有在推开门才给 reward。
描述很简单,但是实际上机器人首先需要学习到控制 motor,通过控制 motor 来移动,然后才是导航,推门的动作。这样的流程其实是比较复杂的,如果单纯随机的话,可能机器人只会在原地打滚。
因此就会有一个简单的想法,通过额外的 reward 来帮助 agent 学习,比如奖励移动,站立。那么 agent 就容易获得 dense 的 reward,学习到移动,站立。
但是这样的在实际训练中其实是不自然的,同时可能会影响,甚至损害 agent 在原先任务上的学习。比如:如果给予移动比较大的 reward,而出现成功开门的几率又比较小,那么 agent 可能会被诱导成一直在移动的 agent。
那么直观地,我们肯定想要权衡两者间的平衡,一种做法就是 Exploration Curriculum:在开始的时候给予 dense reward 来帮助学习,让 agent 学习到一些 basic 的动作,比如移动,站立,同时可以帮助提高真正想学习任务 reward 出现的几率,这个 reward 被称为 exploration reward。
随着训练,把 exploration reward 减少到 0,即不断减小下面的 αt ,所以只剩下真正任务的 reward,那么接着学,优化的就是真正想要学习的任务了:
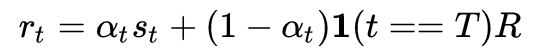
Opponent Sampling
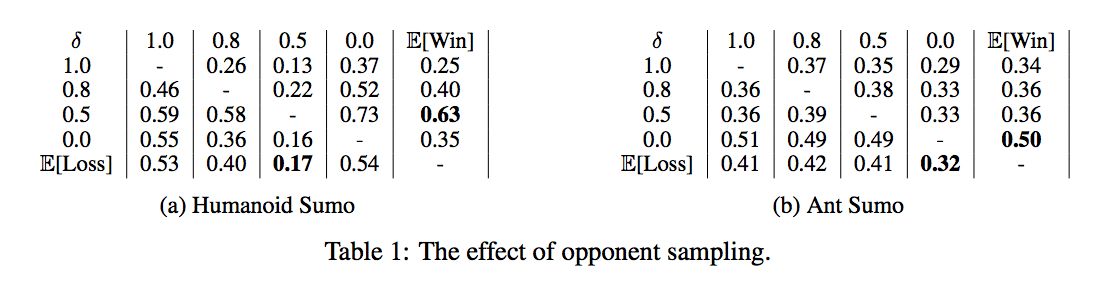
正如上面说到的,太难对手,你太难学,太简单的对手,你也学的菜。那么该如何利用对手来学习出一个复杂的 task 的 policy 呢?
在实际学习的时候,可能出现一个 agent 先学的比较好,那么另外一个 agent 可能完全学不到,或者不收敛,这种情况出现的比较多。也就是上面的:太难的对手出现的几率会多一些。
所以我们会想对手不要那么难就好了,一种想法是:现在他比较难,但是他之前可能比较简单啊!
这里给了一个解决方案:就是在每个 rollout 开始的时候,选择 random old version 的对手来学习。这样的效果能学习得更稳定,策略更鲁棒。
Note that for self-play this means that the policy at any time should be able to defeat random older versions of itself, thus ensuring continual learning.
Training Competitive Agents
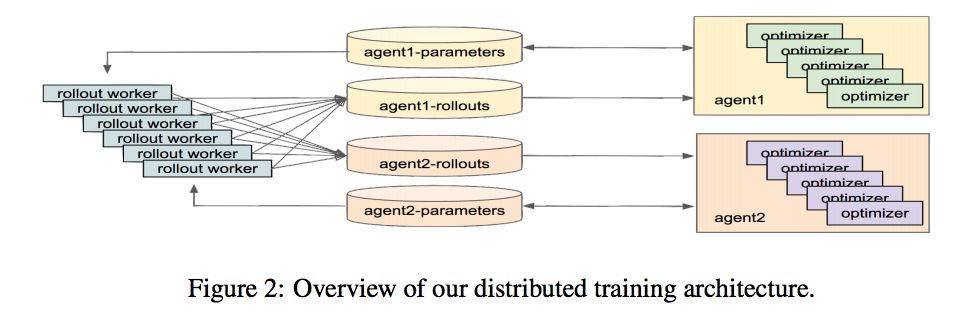
这篇文章采用 distrubuted PPO 对 agent 做优化。
一个比较有价值的点是:PG 在 multiagent 的设置下更容易受到方差的影响而不稳定,为了解决这个不稳定的问题,MADDPG 用了一个中心式的 critic,但是这样在训练的时候就要求知道 global 的 state 和 joint action,加入了额外的限制条件。
但是用 independent 训练时,又容易有方差的问题。为了缓解方差的问题,这里的采用非常大的 batch size 的 distributed PPO 来做 independent 的 training。
因为大的 batch 包含的东西更多,agent 的 policy 稍微改变失误就会对 PG 造成比较大影响,另外就是比较大的 batch 能够包含更久的信息,agent 不会特别快收敛当前的 policy,所以还能帮助探索。
两个网络结构
MLP:两个 128 个 unit 的 hidden layer(激活函数没有说)
LSTM:
128 个 unit 的全连接,使用 RELU
128 个 hidden state 的 LSTM
个数为 action dimension 的全连接
策略的细节
使用 Gaussian policy,其中 mean,diagonal covariance matrix 为网络的输出,采样后 clipped 到合理的 control range。
在 run-to-goal 和 you-shall-not-pass 中使用 MLP policy 与 value function,在 sumo 和 kick-and-defend 中使用 LSTM policy 与 value function(下面会提到)。
主要的原因是 MLP 在使用 LSTM 那两个任务不好。使用 LSTM 时,我们采用截断的 BPTT,在 10 个 timesteps 采取截断。
policy 与 value function 采用不同的参数,即不共享参数。
训练细节
1. PPO 使用 clipped objective, ϵ=0.2,γ=0.995,λ=0.95。
2. 每个 agent 并行做多个 rollout,各自优化,collect 409600 samples from the parallel rollouts.
3. PPO training in mini-batches consisting of 5120 samples.
4. For MLP policies we did 6 epochs of SGD per iteration and for LSTM policies we did 3 epochs.
5. don’t use any entropy bonus,使用 L2。
6. 每个 agent 采用 4 个 GPU 来训练。
5. 像 synchronous actor critic,在一整个 rollout 上计算 GAE,因为是在最后才给的 reward。
6. 优化器:Adam, lr 0.001
7. co-efficient αt in eq. 1 for the exploration reward is annealed to 0 in 500 iterations for all the environments except for kick-and-defend in which it is annealed in 1000 iterations.
Competitive Environments

agent 的 body 如下:
1. ant: 12 DoF,8 actuated joints
2. humanoid: 23 DoF,17 actuated joints 形状如上图
对于 ant body 的 observations:
all the joint angles of the agent its velocity of all its joints the contact forces acting on the body the relative position and all the joint angles for the opponent.
对于 humanoid body 的 observations:
在 ant body 的基础上,centre-of-mass based inertia, mass, velocity and the actuator forces for the body.
四个环境:
1. run to goal:感觉就是方形的相扑,但其目标是到达另外一边。先到达的 reward+1000,晚到达的 reward-1000,如果都没有达到,那么都 -1000。
2. you shall not pass:就是把 1 的内容稍作改动,目标是阻止对方到达对面。如果成功阻止了,而且最后成功阻止的 agent 还站着的话,阻止的 agent 的 reward+1000,如果阻止的 agent 没有站着的话,它的 rewerd 为 0,然后那个被阻止的 agent reward 为 -1000。如果 agent 过去了,他的 reward 为 1000,这个阻止失败的 agent reward 为 -1000。
3. sumo:就是相扑,圆形的场地,目标是让对方摔倒或者推出场地。赢的获得 +1000 的 reward,输的获得 -1000 的 reward。如果没有输赢,则都是 -1000。
4. kick and defend:射门。一个 agent 射门,一个 agent 防守。射门的地方有 6 个 unit 宽,成功的射门或者防守获得 +1000,失败的获得 -1000。防守的 agent 不能离开球太远,太远的话,给予 -1000 的惩罚,另外如果防守成功,而且碰到球,再给予 +500 的奖励,如果最后还站着,再给 +500。
对于相扑的环境,还有额外的 observations:
torso’s orientation vector the distance from the edge of the ring of all the agent the time remaining in the game.
对于点球的环境,还有额外的 observations:
the relative position of the ball from the agent the relative distance of the ball from goal the relative position of the ball from the two goal posts.
Experiments
使用 Exploration Curriculum 效果更好。
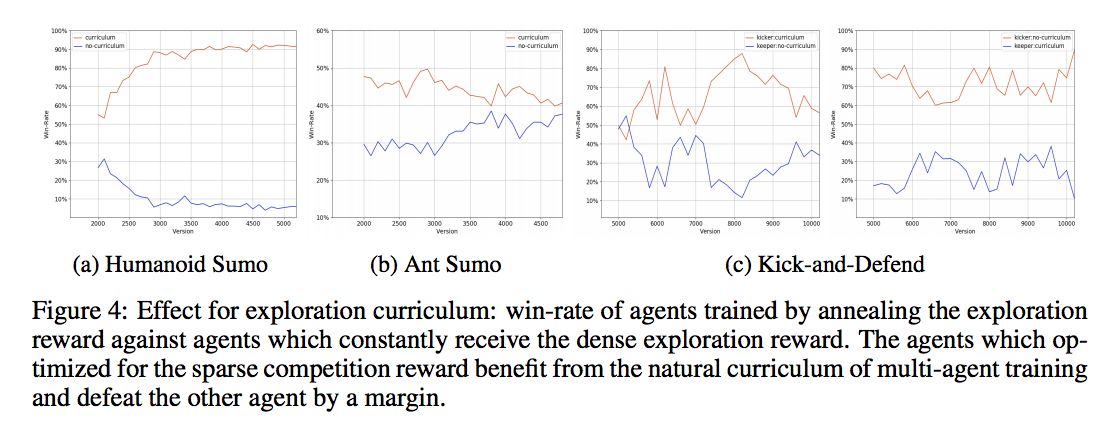
不同 opponent sampling 的影响,ant 一直都是均匀的好,因为 ant 简单,random 的防守其实也不错,但是 human 形状的从一半开始采样好,因为 human 更难,随机不好。
另外为了验证是否 over fitting 对手策略,这里做了一个实验就是踢球的环境,固定球训练,然后在测试的时候移动球,发现 agent 不能很好的泛化,只在球的一个位置好:
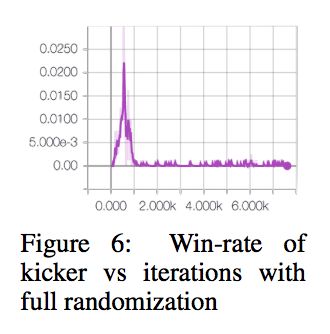
但是开始一直随机又学不好,因为空间太大,所以这里类似 exploration reward的做法,开始小小的随机,随着训练随机形增大。

△ 戳我领取新年礼物
参与方式
1. 长按识别下方二维码参与投票
2. 文末留言你喜欢某篇论文的原因
3. 分享本文到朋友圈并截图发至后台
截止时间
2018年1月24日0点0分
福利清单
PaperWeekly定制手机壳 x 3份
PaperWeekly定制笔记本 x 5份
PaperWeekly定制行李牌 x 10份

△ 我们长这样哦~
长按扫描二维码,参与投票!
▼

 # 高 能 提 醒 #
# 高 能 提 醒 #
1. 为了方便大家在投票过程中查看论文详情,请勿使用微信内置浏览器。点击页面右上角的“…”按钮,在手机浏览器中打开表单。
2. 本次评选包含自然语言处理和计算机视觉两大方向,请在你所选择的参与方向下勾选3-10篇论文。
3. 获奖名单将于1月25日公布,其中5位由小编根据文末留言选取,其他13位采用随机抽取,礼物随机发放。
长按扫描二维码,马上投票!
▼

关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。

▽ 点击 | 阅读原文 | 查看作者知乎主页
最后
以上就是调皮马里奥最近收集整理的关于三招武林绝学带你玩转「强化学习」以彼之道还施彼身小无相功左右互搏:self-play的全部内容,更多相关三招武林绝学带你玩转「强化学习」以彼之道还施彼身小无相功左右互搏内容请搜索靠谱客的其他文章。








发表评论 取消回复