目录
1 设计思路
1.1 AvlTree.h的私有部分
1.2 AvlTree.h的公有部分
1.3 测试程序
1.3.1 变量
1.3.2 测试过程
2 理论分析
3 数值结果分析
3.1 K与运行效率
3.1.1 数据
3.1.2 拟合曲线
3.1.3 终端输出
3.2 n与运行效率
3.2.1 数据
3.2.2 拟合曲线
3.2.3 终端输出

1 设计思路
1.1 AvlTree.h的私有部分
在AvlTree的私有部分中定义printelement函数,实现查找与打印功能。
该函数使用中序遍历算法。若当前节点值在[k1, k2]内,打印出该节点的值,且让计数变量count++;若当前节点值小于k1,则向左子树执行递归调用;若大于k2,则向右子树执行递归调用。
void printelement(Comparable& K1, Comparable& K2, AvlNode* t){
if(t != nullptr){
if(K1 <= t -> element){
printelement(K1, K2, t -> left);
}
if(K1 <= t -> element && t -> element <= K2){
cout << t -> element << endl;
count ++;
}
if(t -> element <= K2){
printelement(K1, K2, t -> right);
}
}
}
1.2 AvlTree.h的公有部分
在AvlTree的公有部分中定义printelement函数,方便测试程序调用。声明count,并定义numberofK函数,用于记录关键字被打印的个数。
double count = 0;
void printelement(Comparable& K1, Comparable& K2){
printelement(K1, K2, root);
}
double numberofK(){
return count;
}
1.3 测试程序
1.3.1 变量
double k1; //区间最小值 double k2; //区间最大值 double K; //所打印的关键字的个数 double wholetime; //函数总运行时间 double num; //元素总个数 double lower; //元素最小值 double upper; //元素最大值
1.3.2 测试过程
std::vector<double> a; //声明数组
AvlTree <double> AT; //创建AvlTree对象
for(double i = lower; i < upper; i++){
//将范围从lower到upper的元素存入输入
a.push_back(i);
}
for(double i = 0; i < num; i++){
//将数组中的元素插入到AvlTree
AT.insert(a[i]);
}
clock_t startTime = clock(); //函数执行前时刻
AT.printelement(k1, k2); //执行函数
clock_t endTime = clock(); //函数执行后时刻
//通过函数获取所打印的关键字的个数
K = AT.numberofK();
wholetime =
double(endTime - startTime) / CLOCKS_PER_SEC;
cout << "打印的关键字的个数K为" << K << "个" << endl;
cout << "总个数n为" << num << endl;
cout << "运行时间为" << wholetime << "s" << endl;
2 理论分析
如果当前节点的值在[k1, k2]之间,则该节点之后部分将执行中序遍历,由于有K个节点的值在此范围内,则总的中序遍历的时间复杂度为O(K)。而对于那些值不在[k1,k2]范围内的节点,将会一直进行递归查找,此时所用的时间与树的深度成正比。
令D(N)是具有N个节点的某棵树T的内部路径长,D(1)=0。一棵N节点树是由一棵i节点左子树和一棵(N-i-1)节点右子树以及深度0处的一个根节点组成的,其中0≤i<N,D(i)为根的左子树的内部路径长。但是在原树中,所有这些节点都要加深一层。同样的结论对于右子树也是成立的。
由此,我们得到递推关系:D(N)=D(i)+D(N-i-1)+N-1
由于所有子树的大小都是等可能地出现,那么D(i)和D(N-i-1)的平均值都是
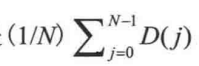
,于是得到
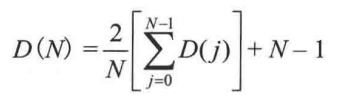
,得到的平均值D(N) = O(NlogN)。因此,任意节点的期望深度为O(logN)。因此,该算法的平均运行时间界为O(K+logN)。
3 数值结果分析
3.1 K与运行效率
3.1.1 数据
| 4001 | 0.017158 |
| 20001 | 0.156204 |
| 60001 | 0.460664 |
| 200001 | 0.784702 |
| 400001 | 1.97195 |
| 800001 | 3.51683 |
| 1800000 | 8.09652 |
| 3400000 | 14.1082 |
| 4000000 | 18.2855 |
| 5000000 | 24.1056 |
| 6000000 | 25.0521 |
| 8000000 | 34.6599 |
| 12000000 | 55.1643 |
| 14000000 | 62.8787 |
| 16000000 | 79.656 |
| 18000000 | 90.4076 |
3.1.2 拟合曲线
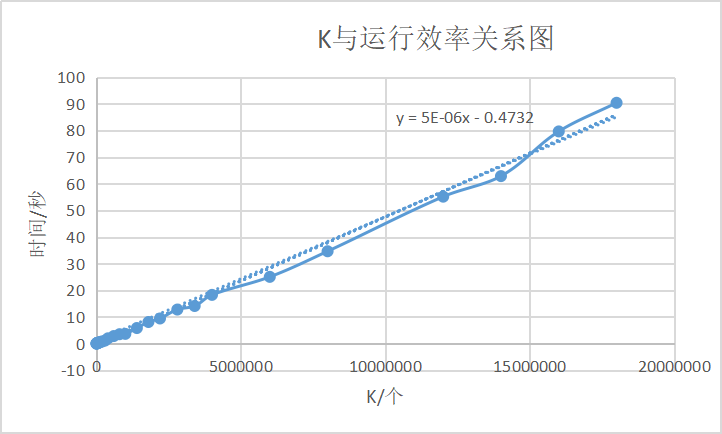
设定元素总数n = 20000000,且保持不变。改变打印出关键字的个数K。根据实验结果拟合出的曲线,可以发现此时K与运行效率为线性关系,符合理论值O(K)。
3.1.3 终端输出
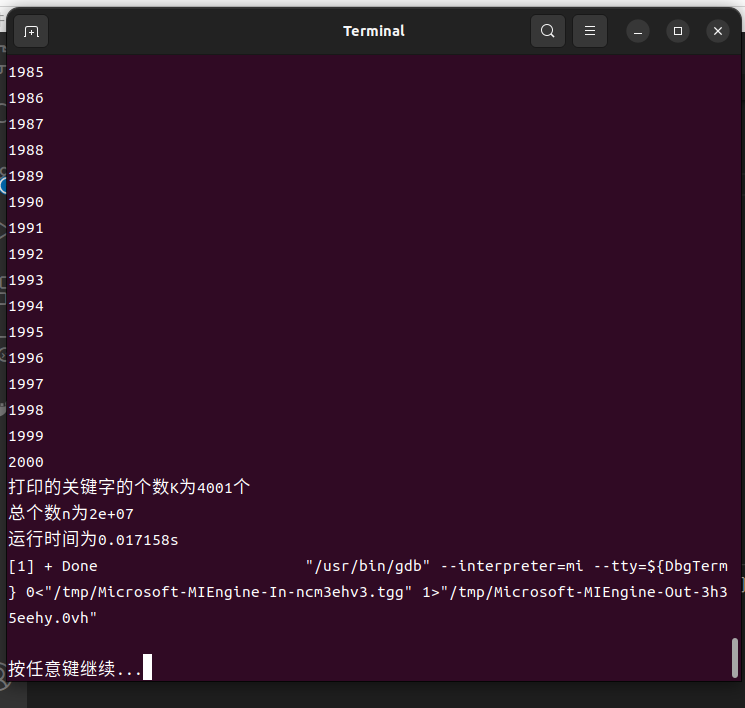
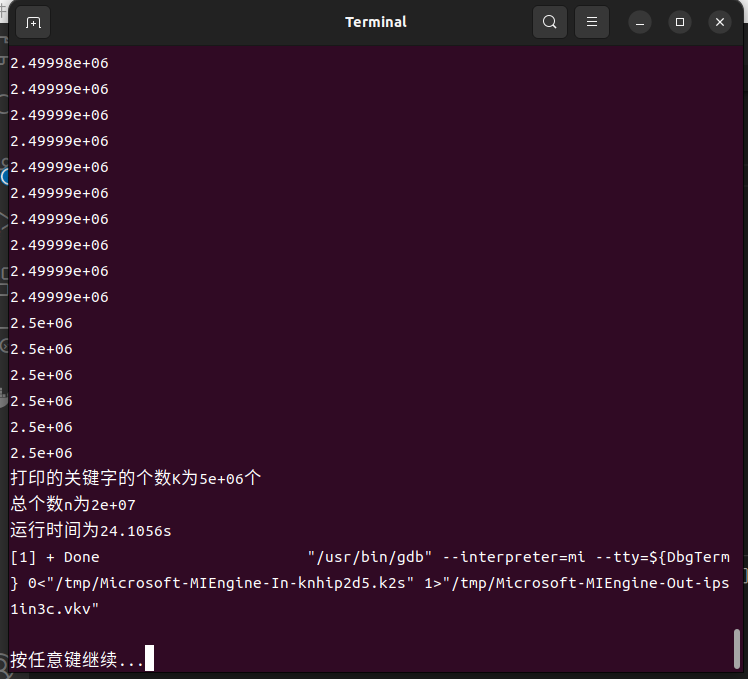
3.2 n与运行效率
3.2.1 数据
| 100000 | 0.000669 |
| 500000 | 0.001371 |
| 1500000 | 0.00262 |
| 3000000 | 0.0037 |
| 5000000 | 0.0042 |
| 10000000 | 0.005021 |
| 15000000 | 0.005269 |
| 20000000 | 0.005685 |
| 30000000 | 0.006133 |
3.2.2 拟合曲线
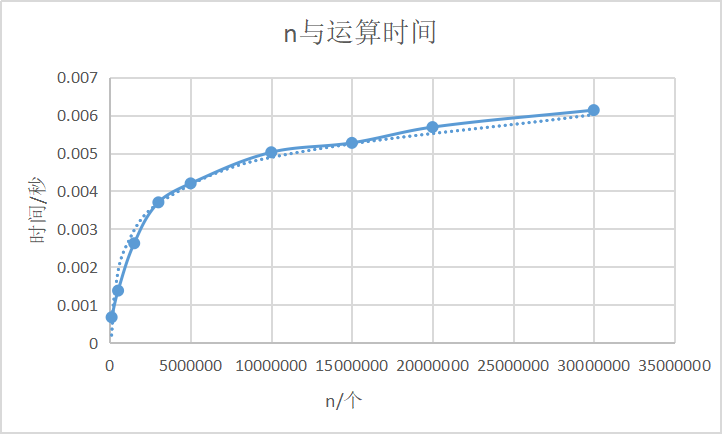
设定打印出的关键字个数K = 101,且保持不变。改变元素总数n,根据实验结果拟合出的曲线,发现n与运行时间基本符合对数关系,与理论值O(logn)较为接近。
3.2.3 终端输出
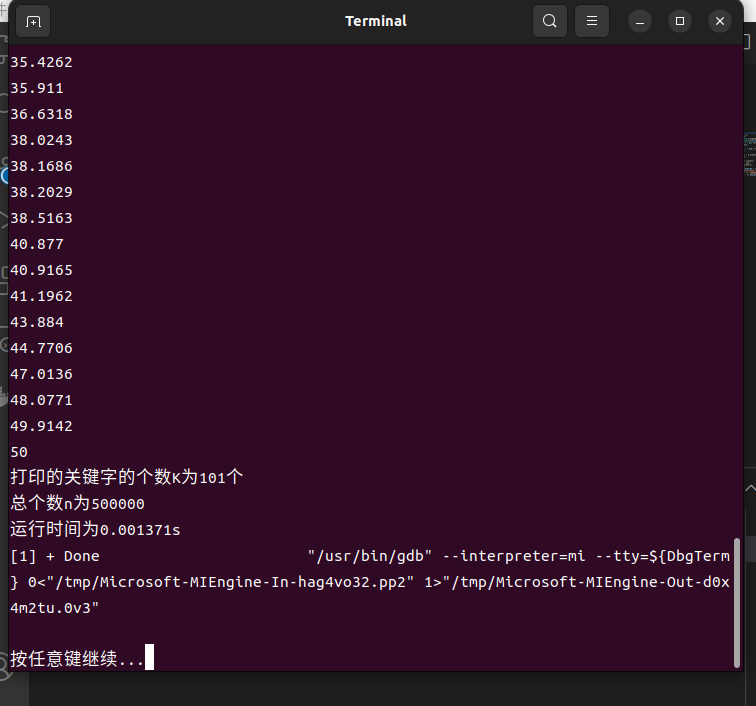
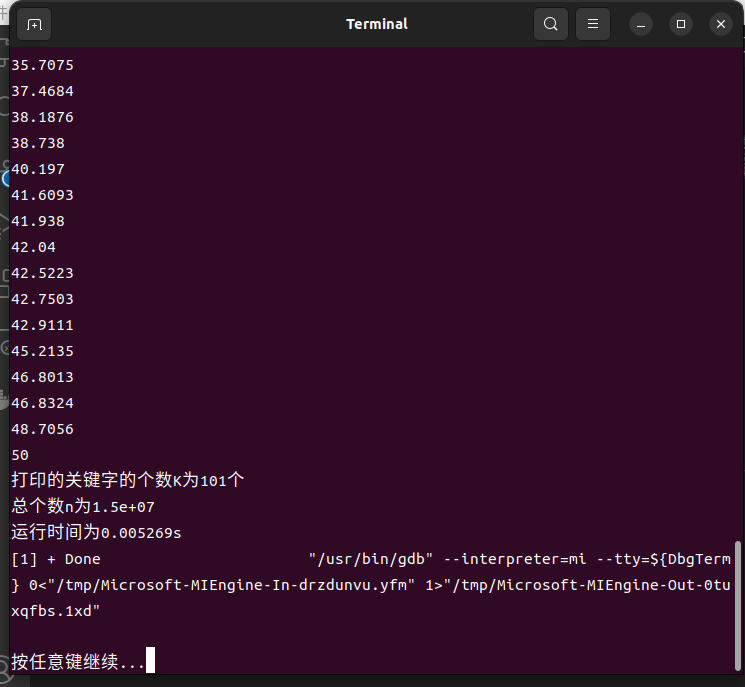
最后
以上就是时尚大白最近收集整理的关于二叉树习题1 设计思路2 理论分析3 数值结果分析的全部内容,更多相关二叉树习题1内容请搜索靠谱客的其他文章。








发表评论 取消回复