解法一

一、分析

采用二维数组的前缀和来算。

二、时间复杂度

O(n^4)

三、代码

#include <iostream>
using namespace std;

const int maxN = 800 + 5;
int n, m, k, sum[maxN][maxN];
char  a[maxN][maxN];

void input()
{
    cin >> n >> m >> k;
    for(int r=1; r<=n; r++)
    {
        for(int c=1; c<=m; c++)
        {
            cin >> a[r][c];
        }
    }
}

//求二维数组前缀和
void getPreSum()
{
	for(int r=1; r<=n; r++)
    {
        for(int c=1; c<=m; c++)
        {
            sum[r][c] = sum[r-1][c] + sum[r][c-1] - sum[r-1][c-1] + (a[r][c] == '.');
        }
    }
}

int getSum(int r1, int c1, int r2, int c2)
{
    return sum[r2][c2] - sum[r1-1][c2] - sum[r2][c1-1] + sum[r1-1][c1-1];
}

int main()
{
    //freopen("T5.in", "r", stdin);

    input();
    getPreSum();

    const int INF = 2100000000;
    int minArea = INF;

    for(int r1 = 1; r1 <= n; r1++)
    {
        for(int c1 = 1; c1 <= m; c1++)
        {
            for(int r2 = r1; r2 <= n; r2++)
            {
                for(int c2 = c1; c2 <= m; c2++)
                {
                    if(getSum(r1, c1, r2, c2) >= k && (r2 - r1 + 1) * (c2 - c1 + 1) < minArea)
                    {
                        minArea = (r2 - r1 + 1) * (c2 - c1 + 1);
                    }
                }
            }
        }
    }

    if(minArea == INF)
    {
        cout << "No Solution";
    }
    else
    {
        cout << minArea;
    }

    return 0;
}

解法二： 尺取法

一、分析

我们可以按照先列后行的顺序来枚举。列有15种情况：
从第1列到第1列（只有一列），从第1列到第2列，从第1列到第3列，从第1列到第4列，从第1列到第5列；
从第2列到第2列，从第2列到第3列，从第2列到第4列，从第2列到第5例；
从第3列到第3列，从第3列到第4列，从第3列到第5列；
从第4列到第4列，从第4列到第5列；
从第5列到第5列。
对于这15种枚举列的情况，再分别枚举行。

以样例2中的数据为例，枚举过程如下：

（一）从第1列到第1列，L = 1, R = 1
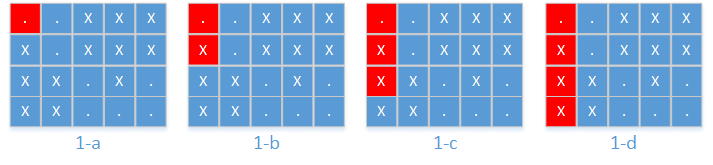
（1）从第1行到第1行，up = 1, down = 1，只有一个空座，不够k 个。如图1-a所示。
（2）从第1行到第2行，up = 1, down = 2，只有一个空座，不够k 个。如图1-b所示。
（3）从第1行到第3行，up = 1, down = 3，只有一个空座，不够k 个。如图1-c所示。
（4）从第1行到第4行，up = 1, down = 4，只有一个空座，不够k 个。如图1-d所示。
所以L = 1, R = 1，无论取几行，都没有答案。

（二）从第1列到第2列，L = 1, R = 2
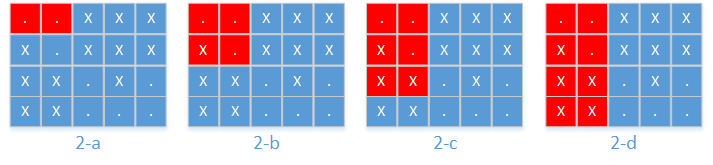
（1）从第1行到第1行，up = 1, down = 1，有两个空座，不够k个。如图2-a所示。
（2）从第1行到第2行，up = 1, down = 2，有三个空座，不够k个。如图2-b所示。
（3）从第1行到第3行，up = 1, down = 3，有三个空座，不够k个。如图2-c所示。
（4）从第1行到第4行，up = 1, down = 4，有三个空座，不够k个。如图2-d所示。

（三）从第1列到第3列，L = 1, R =3
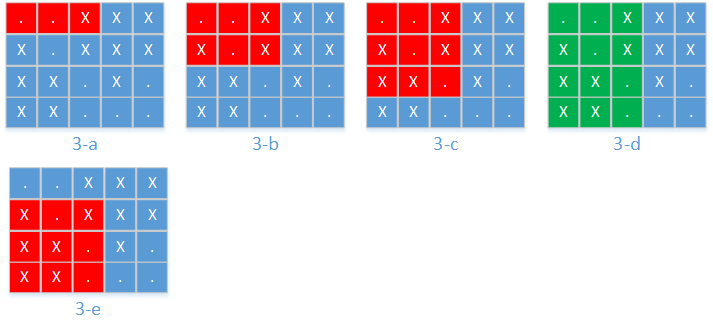
（1）从第1行到第1行，up = 1, down = 1，有两个空座，不够k个。如图3-a所示。
（2）从第1行到第2行，up = 1, down = 2，有三个空座，不够k个。如图3-b所示。
（3）从第1行到第3行，up = 1, down = 3，有四个空座，不够k个。如图3-c所示。
（4）从第1行到第4行，up = 1, down = 4，有五个空座，够k个。此时的面积为3 * 4 =12。要尝试减少行数来确定有没有更小的面积。如图3-d所示。
（5）从第2行到第4行，up = 2, down = 4，有三个空座，不够k个。因此，从第3行到第4行和从第4行到第4行，都不用再枚举。因为肯定不够k个。如图3-e所示。

（四）从第1列到第4列，L = 1, R = 4
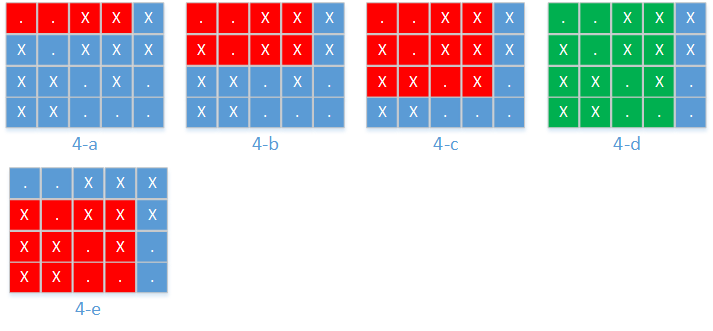
（1）从第1行到第1行，up = 1, down = 1，有两个空座，不够k个。如图4-a所示。
（2）从第1行到第2行，up = 1, down = 2，有三个空座，不够k个。如图4-b所示。
（3）从第1行到第3行，up = 1, down = 3，有四个空座，不够k个。如图4-c所示。
（4）从第1行到第4行，up = 1, down = 4，有六个空座，够k个。此时的面积为4 * 4 =16，与上面的12比较，最小的面积仍为12。要尝试减少行数来确定有没有更小的面积。如图4-d所示。
（5）从第2行到第4行，up = 2, down = 4，有四个空座，不够k个。因此，从第3行到第4行和从第4行到第4行，都不用再枚举。因为肯定不够k个。如图4-e所示。

（五）从第1列到第5列，L = 1, R = 5
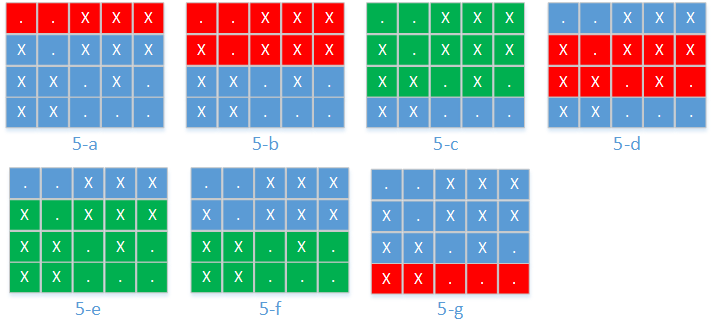
（1）从第1行到第1行，up = 1, down = 1，有两个空座，不够k个。如图5-a所示。
（2）从第1行到第2行，up = 1, down = 2，有三个空座，不够k个。如图5-b所示。
（3）从第1行到第3行，up = 1, down = 3，有五个空座，够k个。面积为3 * 5 = 15，与最小面积12比较，最小值仍为12。不需要继续枚举从第1行到第4行，因为座位肯定够且面积会更大。如图5-c所示。
（4）从第2行到第3行，up = 2, down = 3，有三个空座，不够k个。如图5-d所示。
（5）从第2行到第4行，up = 2, down = 4, 有六个空座，够k个。当前面积为15，最小面积仍为12。如图5-e所示。
（6）从第3行到第4行，up = 3, down = 4，有五个座位，够k个，当前面积为10，最小面积更新为10。如图5-f所示。
（7）从第4行到第4行，up = 4, down = 4，有三个座位，不够k个。如图5-g所示。

（六）从第2列到第2列，略

（七）从第2列到第3列，略

（八）从第2列到第4列，略

（九）从第2列到第5列，略

（十）从第3列到第3列，略

（十一）从第3列到第4列，略

（十二）从第3列到第5列，略

（十三）从第4列到第4列，略

（十四）从第4列到第5列，略

（十五）从第5列到第5列，略

二、时间复杂度

O(n^3)

三、代码

#include<bits/stdc++.h>
using namespace std;

char seat; //'X'表示已被预订，'.'表示空座
const int maxN = 800 + 10;
int n, m, k, totalEmpty, ans = 1e9, a[maxN][maxN];

void getSectionSum(int L, int R)
{
    int emptySeats = 0, up = 1, down = 1;
    for(; up <= n; up++)
    {
        for(; down <= n && emptySeats < k; down++)
        {
            emptySeats += a[down][R] - a[down][L - 1];
        }

        if(emptySeats < k)
        {
            break;
        }

        //down最后又自加了一次，所以down-up不用再+1
        ans = min(ans,(R - L + 1) * (down - up));
        emptySeats -= a[up][R] - a[up][L - 1];
    }
}

int main()
{
    //freopen("T5.in", "r", stdin);
    cin >> n >> m >> k;
    for(int i = 1; i <= m; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin>>seat;
            totalEmpty += (seat == '.'); //总共有多少个空座
            a[i][j] = a[i][j - 1] + (seat == '.');
        }
    }

    if(totalEmpty < k)
    {
        cout<<"No Solution"<<endl;
        return 0;
    }

    for(int L = 1; L <= n; L++)
    {
        for(int R = L; R <= m; R++)
        {
            getSectionSum(L, R);
        }
    }

    cout<<ans<<endl;

    return 0;
}

了解中小学信息学竞赛请加微信307591841（QQ同号）

最后

以上就是土豪高山为你收集整理的上海青少年算法竞赛6月月赛丙组T5题解报告解法一解法二： 尺取法的全部内容，希望文章能够帮你解决上海青少年算法竞赛6月月赛丙组T5题解报告解法一解法二： 尺取法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。