普通kd树的创建

算法逻辑

我们采用面向对象编程的方法。通过关键字class创建一个名为kdTree的类，在类kdTree中定义一些属性与方法（可以理解成c语言中的函数）。

#面向对象编程
class kdTree:
    def __init__(self, parent_code):
        """
        把我们认为对象self必须有的属性通过__init__方法绑定到self上
        """
        self.nodedata = None #当前结点的坐标值，二维数据
        self.split = None #分割平面的方向轴代号,0代表沿x轴,1代表沿y轴
        self.range = None #分割临界值
        self.left = None #左子树(kdTree实例)
        self.right = None #右子树(kdTree实例)
        self.parent = parent_code #当前结点的父结点
        self.left_tree_data = None #存储当前结点的左子树结点的坐标
        self.right_tree_data = None #存储当前结点的右子树结点的坐标
        self.if_invited = False #记录当前结点是否被访问过

    """
    def print(self):
        输出当前结点信息
        print(self.nodedata, self.split, self.range)
    """

    def get_split_axis(self, all_data):
        """
        根据每轴坐标值的方差决定分割轴
        """

    def get_range(self, split_axis, all_data):
        """
        获取对应分割轴的中位数据，把中位数据也叫分割临界值
        """

    def get_node_tree_data(self, all_data):
        """
        将当前数据划分为左、右子树及得到当前子树的根结点
        """

    def create_next_node(self, all_data):
        """
        迭代创建结点，生成kd树
        """

    def plot_kdTree(self):
        """
        在图上画出树形结构的递归迭代过程
        """

后面我们只需根据一定的逻辑在类kdTree中调用这些属性及方法。

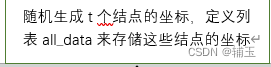
算法的逻辑框图如下（程序运行中存在递归调用）：

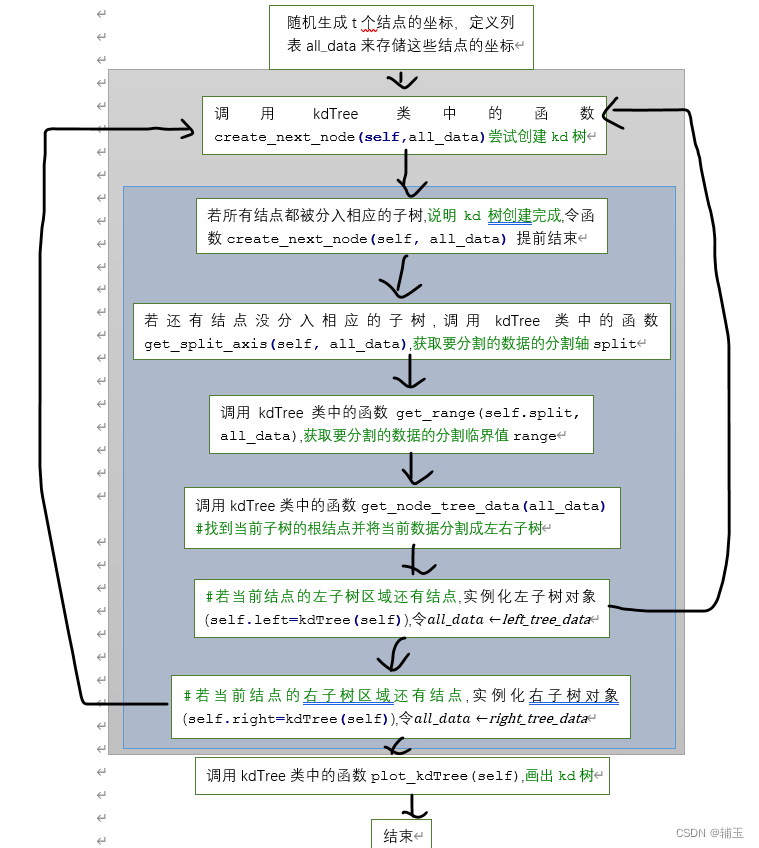
为什么说存在递归调用？程序框图中被浅蓝色框圈起来的6个板块事实上就是函数create_next_node(self, all_data)的一部分。从框图中可以看出，程序在还没有跳出函数create_next_node(self, all_data)时又要重新调用函数create_next_node，这就是函数的递归调用。

kd树是一种树形结构，因此它可以通过递归的方式来生成。

代码分块剖析

1、

test_array = 10 * np.random.random([30,2]) #先随机生成30个结点

2、

对函数create_next_node(self, all_data)的首次调用不属于递归调用。

my_kd_tree = kdTree(None) #实例化对象
my_kd_tree.create_next_node(test_array) #生成kd树

3、

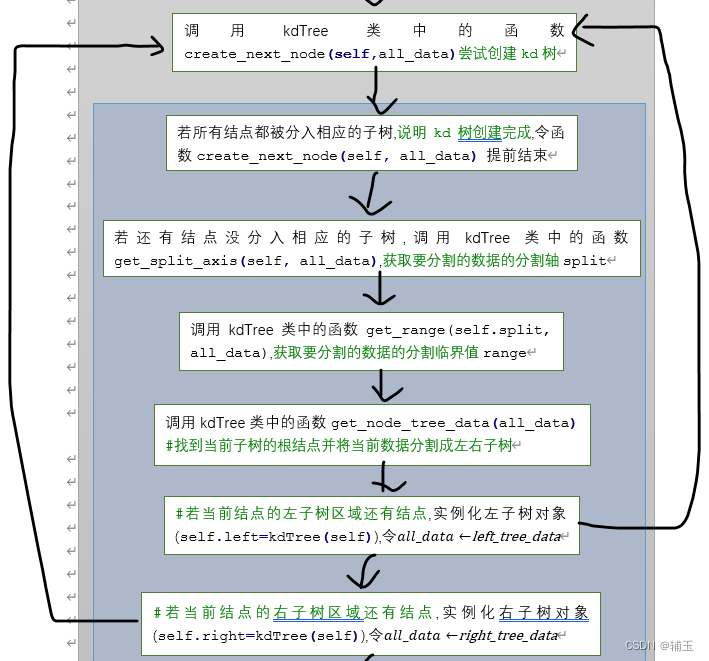
在程序还未跳出函数create_next_node(self, all_data)时再次调用函数create_next_node属于递归调用。

def create_next_node(self, all_data):
        """
        迭代创建结点，生成kd树
        """
        if all_data.shape[0] == 0: #若所有结点都被编入相应的子树
            print("The creation of kd tree is finished!") #说明kd树创建完成
            return None #提前结束函数运行
        #若还有结点没被编入相应的子树
        self.split = self.get_split_axis(all_data) #获取要分割的数据的分割轴
        self.range = self.get_range(self.split, all_data) #获取当前数据沿分割轴的临界值
        self.get_node_tree_data(all_data) #将当前数据分割并找到当前子树的根结点
        if self.left_tree_data.shape[0] != 0: #若当前结点的左子树区域还有结点(说明kd树还没建完)
            self.left = kdTree(self) #先实例化左子树对象
            self.left.create_next_node(self.left_tree_data) #在当前根结点的左子树区域继续建立子树
        if self.right_tree_data.shape[0] != 0: #若当前根结点的右子树区域还有结点(说明kd树还没建完)
            self.right = kdTree(self) #先实例化右子树对象
            self.right.create_next_node(self.right_tree_data) #在当前根结点的右子树区域继续建立子树

完整代码

#导入可能需要的计算库
import numpy as np
import matplotlib.pyplot as plt

#面向对象编程
class kdTree:
    def __init__(self, parent_code):
        """
        结点初始化。初始化后调用该对象时无需多次传递参数。
        若不进行结点初始化，class就相当于c语言中一个单纯的函数，调用时必须输入该有的参数
        """
        self.nodedata = None #当前结点的坐标值，二维数据
        self.split = None #分割平面的方向轴代号,0代表沿x轴,1代表沿y轴
        self.range = None #分割临界值
        self.left = None #左子树(kdTree实例)
        self.right = None #右子树(kdTree实例)
        self.parent = parent_code #当前结点的父结点
        self.left_tree_data = None #存储当前结点的左子树结点的坐标
        self.right_tree_data = None #存储当前结点的右子树结点的坐标
        self.if_invited = False #记录当前结点是否被访问过

    """
    def print(self):
        输出当前结点信息
        print(self.nodedata, self.split, self.range)
    """

    def get_split_axis(self, all_data):
        """
        根据每轴坐标值的方差决定分割轴
        """
        var_all_data = np.var(all_data, axis=0) #axis = 0表示沿列的方差，axis = 1表示沿行的方差
        if var_all_data[0] > var_all_data[1]: #若沿x轴方差大于沿y轴的方差
            return 0 #则选分割轴为x轴
        else:
            return 1 #否则选y轴为分割轴

    def get_range(self, split_axis, all_data):
        """
        获取对应分割轴的中位数据，把中位数据也叫分割临界值
        """
        split_all_data = all_data[:, split_axis] #x[:,n]表示取x[]中每个元素的第n个数据
        data_count = split_all_data.shape[0] #shape函数会读取矩阵指定维的长度
        middle_index = int(data_count/2) #获取分割轴中位数据的索引
        sort_split_all_data = np.sort(split_all_data) #将分割轴的坐标值排序
        range_data = sort_split_all_data[middle_index] #得到要分割的结点中沿分割轴方向的中位数据
        return range_data

    def get_node_tree_data(self, all_data):
        """
        将当前数据划分为左、右子树及得到当前子树的根结点
        """
        data_count = all_data.shape[0] #获取要划分的结点的个数
        ls_left_dat = [] #创建空列表来存储左子树的结点数据
        ls_right_dat = [] #创建空列表来存储右子树的结点数据
        for i in range(data_count): #通过循环将每个数据点分到对应的子树
            now_data = all_data[i] #先取得当前数据点的值
            if now_data[self.split] < self.range: #若当前结点沿分割轴的坐标值<分割临界值
                ls_left_dat.append(now_data) #则将结点编入左子树
            elif now_data[self.split] == self.range and self.nodedata == None: #若当前结点沿分割轴的坐标值=分割临界值
                #且当前子树尚没有根结点
                self.nodedata = now_data #将当前结点作为当前子树的根结点
            else:
                ls_right_dat.append(now_data) #上述两情况都不满足时,将当前结点编入右子树
                """
                刚开始我将第65行写成了 ls_right_dat = now_data(遂在第33行产生报错),
                这样就将ls_right_dat变成了元素为单值的列表，但实际上ls_right_dat本应是存储了
                若个个结点坐标的列表，即ls_right_dat的每个元素都应是代表结点坐标的列表
                """
        self.left_tree_data = np.array(ls_left_dat) #存储当前结点的左子树
        self.right_tree_data = np.array(ls_right_dat) #存储当前结点的右子树

    def create_next_node(self, all_data):
        """
        迭代创建结点，生成kd树
        """
        if all_data.shape[0] == 0: #若所有结点都被编入相应的子树
            print("The creation of kd tree is finished!") #说明kd树创建完成
            return None #提前结束函数运行
        #若还有结点没被编入相应的子树
        self.split = self.get_split_axis(all_data) #获取要分割的数据的分割轴
        self.range = self.get_range(self.split, all_data) #获取当前数据沿分割轴的临界值
        self.get_node_tree_data(all_data) #将当前数据分割并找到当前子树的根结点
        if self.left_tree_data.shape[0] != 0: #若当前结点的左子树区域还有结点(说明kd树还没建完)
            self.left = kdTree(self) #先实例化左子树对象
            self.left.create_next_node(self.left_tree_data) #在当前根结点的左子树区域继续建立子树
        if self.right_tree_data.shape[0] != 0: #若当前根结点的右子树区域还有结点(说明kd树还没建完)
            self.right = kdTree(self) #先实例化右子树对象
            self.right.create_next_node(self.right_tree_data) #在当前根结点的右子树区域继续建立子树

    def plot_kdTree(self):
        """
        在图上画出树形结构的递归迭代过程
        """
        if self.parent == None: #
            plt.figure(dpi=300)
            plt.xlim([0.0, 10.0])
            plt.ylim([0.0, 10.0])
        color = np.random.random(3) #
        if self.left != None: #画当前结点的左子树
            plt.plot([self.nodedata[0], self.left.nodedata[0]], [self.nodedata[1], self.left.nodedata[1]], '-o',
                     color=color)
            plt.arrow(x=self.nodedata[0], y=self.nodedata[1], dx=(self.left.nodedata[0] - self.nodedata[0]) / 2.0,
                      dy=(self.left.nodedata[1] - self.nodedata[1]) / 2.0, color=color, head_width=0.2)
            self.left.plot_kdTree()
        if self.right != None: #画当前结点的左子树
            plt.plot([self.nodedata[0], self.right.nodedata[0]], [self.nodedata[1], self.right.nodedata[1]], '-o',
                     color=color)
            plt.arrow(x=self.nodedata[0], y=self.nodedata[1], dx=(self.right.nodedata[0] - self.nodedata[0]) / 2.0,
                      dy=(self.right.nodedata[1] - self.nodedata[1]) / 2.0, color=color, head_width=0.2)
            self.right.plot_kdTree()

test_array = 10 * np.random.random([30,2]) #先随机生成30个结点
my_kd_tree = kdTree(None) #实例化对象
my_kd_tree.create_next_node(test_array) #生成kd树
my_kd_tree.plot_kdTree()
plt.show()

平衡kd树的创建与搜索

个人理解，平衡kd树与普通kd树的区别在于创建二叉树时，决定分割轴的方式不同。
普通kd树——每建完一个结点后，在剩余结点坐标的k个维度中选择方差最大的维度作为分割轴。
平衡kd树——根据所要创建的结点的深度(depth)来决定分割轴。对深度为j的结点，选择x(l),l=j(mod)k+1为分割轴。

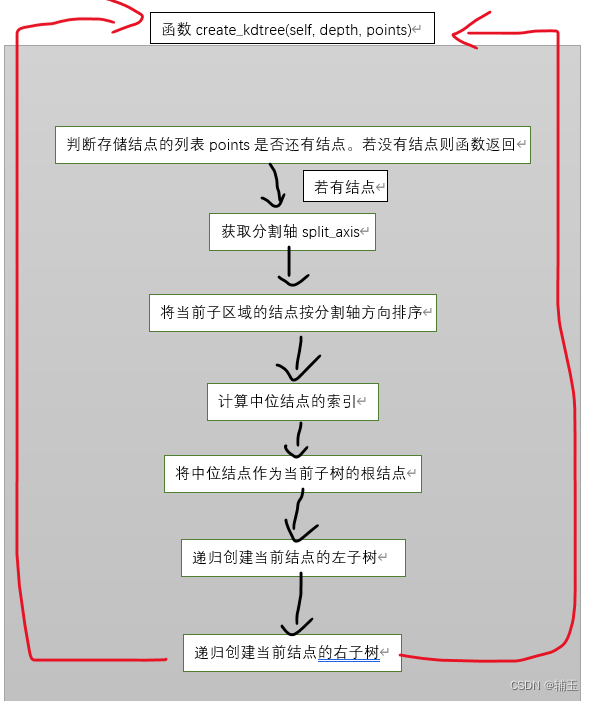
创建树

#导入计算库
import numpy as np
import matplotlib.pyplot as plt

#面向对象编程
class balanced_kdTree:
    def __init__(self, depth, data=None, left=None, right=None):
        """
        把我们认为对象self必须有的属性通过__init__方法绑定到self上
        """
        self.data = data #存储当前子树的所有结点
        """刚开始self.data这个属性是用来存储当前子树的所有结点"""
        self.depth = depth #当前结点的深度
        self.left = left #当前结点的左子树
        self.right = right #当前结点的右子树
        self.if_visited = False #记录当前结点是否被访问过

    def preorder_travel(self):
        """
        前序遍历该平衡kd树
        """
        if self.data == None:
            return #
        print(self.data, self.depth)
        self.left.preorder_travel() #遍历该结点的左子树
        self.right.preorder_travel() #遍历该结点的右子树

    def create_kdtree(self, depth, points):
        if not points: #若列表pints为空,即points中没有结点
            return #函数提前结束
        """
        刚开始我将第29行的if判断写为"if points is none",遂导致列表的越界访问
        因为"if points is none"是判断points是否声明并定义
        """
        k = len(points[0]) #获取结点坐标的维数
        split_axis = depth % k #对深度为j的结点，选择x(l),l=j(mod)k+1为分割轴
        points.sort(key=lambda x: x[split_axis]) #key=lambda x:x[n]表示将待排序对象按第n维度进行排序
        middle_index = len(points)//2 #获取数据中沿分割轴方向的中位数据的索引
        self.data = points[middle_index]
        """将落在分割轴上的结点用self.data来存储"""
        self.left = balanced_kdTree(depth+1, None) #实例化当前结点的左子树对象
        self.left.create_kdtree(depth+1, points[:middle_index]) #创建当前结点的左子树
        self.right = balanced_kdTree(depth+1, None) #实例化当前结点的右子树对象
        self.right.create_kdtree(depth+1, points[middle_index+1:]) #创建当前结点的右子树

tree_root = balanced_kdTree(0, None) #实例化根结点对象
points = 10.0*np.random.random([10,2]) #随机生成10个结点的坐标
#print(type(points)) #确认转化前points的数据类型
points = points.tolist() #将ndarray数组转化为List
#print(type(points)) #确认转化后points的数据类型
"""
numpy.random.random([m,n])产生的是一个ndarray数组,如果不将它转化为list而直接传入函数
crete_kdtree()时会产生报错"ValueError: The truth value of an array with more 
than one element is ambiguous. Use a.any() or a.all()"
"""
tree_root.create_kdtree(0, points) #从根结点tree_root开始生成kd树
tree_root.preorder_travel() #前序遍历整棵树

最近邻搜索

要搜索树，必须要先有树。所以直接在之前创建平衡kd树的代码里加上函数travel_tree就行。

def travel_tree(tree_node, target, k):
    """tree_node为当前结点,target为给定的目标点"""
    """基于平衡kd树的最近邻搜索，找出给定目标点的最近邻点"""

函数逻辑框图如下：

红色的线表示递归调用。

def travel_tree(tree_node, target, k):
    """tree_node为当前结点,target为给定的目标点"""
    """基于平衡kd树的最近邻搜索，找出给定目标点的最近邻点"""
    if not tree_node.data: #先检查当前地址里是否存有结点数据.因为在建立kd树时存在一些空结点
        return [0]*k, float("inf") #[0]*k表示创建长度为k的0数组
    split_axis = tree_node.depth % k #获取当前结点的分割轴
    if target[split_axis] <= tree_node.data[split_axis]: #如果目标点沿分割轴方向的值<当前结点沿分割轴的值(目标离当前结点的左子树更近)
        nearest_point, min_distance = travel_tree(tree_node.left, target, k)
        """向当前结点的左子树区域搜索"""
    else: #若目标点目标离右子树更近
        nearest_point, min_distance = travel_tree(tree_node.right, target, k) #下一个待访问结点为右子结点
        
    a = np.array(target)
    b = np.array(tree_node.data)
    now_distance = np.linalg.norm(a-b) #计算当前点与目标点的欧式距离
    if now_distance < min_distance: #若当前距离<之前记录的最短距离
        min_distance = now_distance #则更新最短距离
        nearest_point = tree_node.data #更新最近点.程序首次运行到此位置时,tree_node即为叶结点
        
    split_axis_dist = abs(target[split_axis]-tree_node.data[split_axis]) #计算目标点与当前点沿分割轴方向的距离
    if split_axis_dist > min_distance:#若以目标点为球心、以目标点与“当前最近点”间距离为半径的超球体与当前结点的父结点的另一子结点区域不相交
        return nearest_point, min_distance #不相交则向上回退
    else: #若相交则另一个子结点对应区域内可能存在距目标点更近的点,则移动到该区域内继续搜索
        if target[split_axis] <= tree_node.data[split_axis]:  #若之前是朝左子结点区域搜索
            next_tree_node = tree_node.right #实例化对象
            """现在就朝向当前结点的右子结点区域搜索"""
        else:  #若之前是朝右子结点区域搜索
            next_tree_node = tree_node.left #实例化对象
            """现在就朝向当前结点的左子结点区域搜索"""
        nearer_point, less_distance = travel_tree(next_tree_node, target, k)
        if less_distance < min_distance: #若在另一子结点区域内找到与目标点更近的结点
            nearest_point = nearer_point
            min_distance =less_distance
        return nearest_point, min_distance

创建平衡kd树与最邻近搜索的完整代码

#导入计算库
import numpy as np
import matplotlib.pyplot as plt

#面向对象编程
class balanced_kdTree:
    def __init__(self, depth, data=None, left=None, right=None):
        """
        把我们认为对象self必须有的属性通过__init__方法绑定到self上
        """
        self.data = data #存储当前子树的所有结点
        """刚开始self.data这个属性是用来存储当前子树的所有结点"""
        self.depth = depth #当前结点的深度
        self.left = left #当前结点的左子树
        self.right = right #当前结点的右子树
        self.if_visited = False #记录当前结点是否被访问过

    def preorder_travel(self):
        """
        前序遍历该平衡kd树
        """
        if self.data == None:
            return #
        print(self.data, self.depth)
        self.left.preorder_travel() #遍历该结点的左子树
        self.right.preorder_travel() #遍历该结点的右子树

    def create_kdtree(self, depth, points):
        if not points: #若列表pints为空,即points中没有结点
            return #函数提前结束
        """
        刚开始我将第29行的if判断写为"if points is none",遂导致列表的越界访问
        因为"if points is none"是判断points是否声明并定义
        """
        k = len(points[0]) #获取结点坐标的维数
        split_axis = depth % k #对深度为j的结点，选择x(l),l=j(mod)k+1为分割轴
        points.sort(key=lambda x: x[split_axis]) #key=lambda x:x[n]表示将待排序对象按第n维度进行排序
        middle_index = len(points)//2 #获取数据中沿分割轴方向的中位数据的索引
        self.data = points[middle_index]
        """将落在分割轴上的结点用self.data来存储"""
        self.left = balanced_kdTree(depth+1, None) #实例化当前结点的左子树对象
        self.left.create_kdtree(depth+1, points[:middle_index]) #创建当前结点的左子树
        self.right = balanced_kdTree(depth+1, None) #实例化当前结点的右子树对象
        self.right.create_kdtree(depth+1, points[middle_index+1:]) #创建当前结点的右子树


def travel_tree(tree_node, target, k):
    """tree_node为当前结点,target为给定的目标点"""
    """基于平衡kd树的最近邻搜索，找出给定目标点的最近邻点"""
    if not tree_node.data: #先检查当前地址里是否存有结点数据.因为在建立kd树存在一些空结点
        return [0]*k, float("inf") #[0]*k表示创建长度为k的0数组
    split_axis = tree_node.depth % k #获取当前结点的分割轴
    if target[split_axis] <= tree_node.data[split_axis]: #如果目标点沿分割轴方向的值<当前结点沿分割轴的值(目标离当前结点的左子树更近)
        nearest_point, min_distance = travel_tree(tree_node.left, target, k)
        """向当前结点的左子树区域搜索"""
    else: #若目标点目标离右子树更近
        nearest_point, min_distance = travel_tree(tree_node.right, target, k) #下一个待访问结点为右子结点
    a = np.array(target)
    b = np.array(tree_node.data)
    now_distance = np.linalg.norm(a-b) #计算当前点与目标点的欧式距离
    if now_distance < min_distance: #若当前距离<之前记录的最短距离
        min_distance = now_distance #则更新最短距离
        nearest_point = tree_node.data #更新最近点.程序首次运行到此位置时,tree_node即为叶结点
    split_axis_dist = abs(target[split_axis]-tree_node.data[split_axis]) #计算目标点与当前点沿分割轴方向的距离
    if split_axis_dist > min_distance:#若以目标点为球心、以目标点与“当前最近点”间距离为半径的超球体与当前结点的父结点的另一子结点区域相交
        return nearest_point, min_distance #不相交则向上回退
    else: #若相交则另一个子结点对应区域内可能存在距目标点更近的点,则移动到该区域内继续搜索
        if target[split_axis] <= tree_node.data[split_axis]:  #若之前是朝左子结点区域搜索
            next_tree_node = tree_node.right #实例化对象
            """现在就朝向当前结点的右子结点区域搜索"""
        else:  #若之前是朝右子结点区域搜索
            next_tree_node = tree_node.left #实例化对象
            """现在就朝向当前结点的左子结点区域搜索"""
        nearer_point, less_distance = travel_tree(next_tree_node, target, k)
        if less_distance < min_distance: #若在另一子结点区域内找到与目标点更近的结点
            nearest_point = nearer_point
            min_distance =less_distance
        return nearest_point, min_distance

tree_root = balanced_kdTree(0, None) #实例化根结点对象
points = 10.0*np.random.random([10,2]) #随机生成10个结点的坐标
#print(type(points)) #确认转化前points的数据类型
points = points.tolist() #将ndarray数组转化为List
#print(type(points)) #确认转化后points的数据类型
"""
numpy.random.random([m,n])产生的是一个ndarray数组,如果不将它转化为list而直接传入函数
crete_kdtree()时会产生报错"ValueError: The truth value of an array with more 
than one element is ambiguous. Use a.any() or a.all()"
"""
tree_root.create_kdtree(0, points) #从根结点tree_root开始生成kd树
tree_root.preorder_travel() #前序遍历整棵树
#print(tree_root.data[0])
#给定目标点,最邻近搜索
target = [7.5, 7.5] #也可调用random函数随机生成目标点
nearest_point, min_distance = travel_tree(tree_root, target, 2)
print(nearest_point,min_distance)

最后

以上就是等待百合为你收集整理的（平衡）kd树的创建与搜索普通kd树的创建平衡kd树的创建与搜索的全部内容，希望文章能够帮你解决（平衡）kd树的创建与搜索普通kd树的创建平衡kd树的创建与搜索所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。