概述
A. The Third Three Number Problem
给出一个数n，找到三个数a，b，c，使得这三个数相互异或得到三个数的和等于n。
思路：其实我的思路是看到第一个样例解释来的，，
然后就想到可以是两个数相同，这样三个数的和就可以转化为两个数的和，而对于偶数，直接用n/2和0异或即可；对于奇数，样例中的1不满足，然后我就直接猜测奇数不可以满足条件，事实证明这个是可以证明的：假设二进制最后一位有k个1和3-k个0，那n的二进制最后一位的奇偶性与k*(3-k)相同，那么n的二进制最后一位应该恒为0。
AC Code：
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=55;
int t,n;
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
if(n&1){
std::cout<<-1<<'n';
continue;
}
std::cout<<n/2<<' '<<n/2<<' '<<0<<'n';
}
return 0;
}B. Almost Ternary Matrix
给出两个偶数，构造一个01矩阵，使得每个方块周围与它不同的方块数是2。
思路：自己画一下试试，会发现我们可以找到一个4*4的单元矩阵，根据这个单位矩阵循环输出即可，单位矩阵如下：
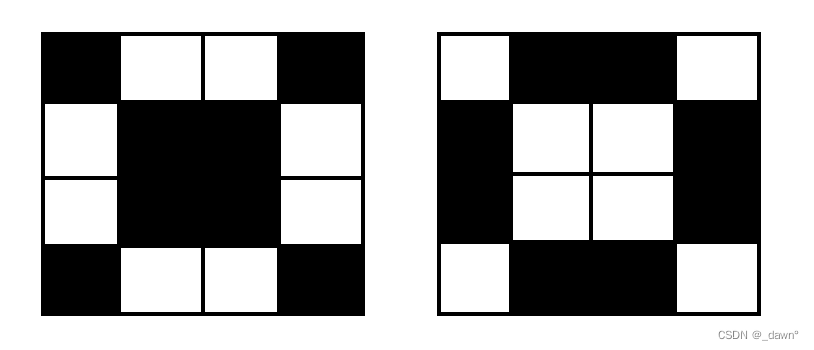
当然，01可以互换，这样代码就很简单了。
AC Code：
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=55;
int t,n,m;
int ans[4][4]={1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1};
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
std::cout<<ans[i%4][j%4]<<" n"[j==m-1];
}
}
}
return 0;
}os：一开始因为怎么写代码想了半天hhhhh
C. The Third Problem
给出一个permutation，不过是从0~n-1，问有多少种重新排列这些数的方法，使得重新排序后的数组对于每个区间的MEX值相等。
思路：看到这个题，大概就是一个排列组合类似的题。根据观察我们可以发现，对于每一个数，只要这个数向前向后都有比该数小的元素存在，那这个数就可以在这个范围内移动，比如样例4：
1 3 7 2 5 0 6 4
比2小的只有0和1，那2就可以在第2到第五个位置移动；3也只能在这个范围内移动，因为比3小的数最向外只能到0和1的位置；而对于在比自己小的数字外围的数字，他们的位置是不能动的，比如4，比它小的0，1，2，3都在前面，很容易理解它的位置如果变化，那一定存在区间的MEX值变化了。根据这个性质，我们可以根据数字大小排序，从小到大枚举，不断更新比当前数小的数的最大范围区间，计算每个数有几种选择位置的方法，相乘即可。当然，0和1作为初始的区间范围，0和1的位置一定不能动。
AC Code：
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n;
int a[N];
struct node{
int id,num;
bool operator<(const node &a) const{
return num<a.num;
}
} e[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
for(int i=1;i<=n;i++){
std::cin>>a[i];
e[i].id=i;
e[i].num=a[i];
}
std::sort(e+1,e+1+n);
int r=-1,l=1e9;
ll ans=1;
for(int i=1;i<=n;i++){
r=std::max(r,e[i].id);
l=std::min(l,e[i].id);
if(i>2&&e[i].id>l&&e[i].id<r){
ans*=(r-l-1-i+3);
ans%=mod;
}
}
std::cout<<ans<<'n';
}
return 0;
}os：二十多分钟搞定前两个题，后面一直在想C，最后五分钟交的hhhh
D. Almost Triple Deletions
给出一个数组，若相邻两个数不同，那可以删去这两个数。最终操作完成后数组中剩余的数都相等，问最多可以保留几个数。
思路：学习大佬的思路，太顶了
我们可以认为操作的最后结果是删除部分连续区间，而对于一个区间[l,r]来说，当且仅当满足下列条件时，可以删除：区间长是偶数；区间中出现最频繁的元素的个数最大为(r-l+1)/2。
必要性一定，证明充分性：
对于出现最频繁的数，一定可以找到一种方法，删去一个和另外一个数，那么还剩下的出现次数t<=(r-l+1)/2-1；如果删除后，这个数还是出现次数最多的，那它还是满足初始条件，依旧可以删除一个该数和另一个数；如果删除后它不是出现次数最多的数了，那一定有另外一个数满足出现次数最多的初始条件，可以删除一个该数和另外一个数，这样就是这个区间内元素之间的相互转化，最后到达平衡时就是两个元素出现次数相等，都等于l/2，这样一定是可以删去的，使得该区间长为0，证毕。
所以我们可以先处理区间可以删除的子区间，cel[l][r]=1，我们定义DP数组f[i]表示从第一个到第i个数，删去部分数达到所有数都等于a[i]后，剩余的个数最大值，f[i]到f[j]的转化方程可以表示为删除区间[j,i]，使得f[i]=f[j]+1。
最后的答案不一定是f[n]，因为最后剩下的数不一定都等于a[n]，所以需要扫一遍取最大值。
数据范围n<=5000，O(n^2)能过。
AC Code：
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=5e3+5;
int t,n;
int a[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
for(int i=1;i<=n;i++){
std::cin>>a[i];
}
int cel[n+1][n+1]={0};
for(int l=1;l<=n;l++){
int cnt[n+1]={0},max=0;
for(int r=l;r<=n;r++){
cnt[a[r]]++;
max=std::max(max,cnt[a[r]]);
if((r-l+1)%2==0&&max*2<=r-l+1)
cel[l][r]=1;
}
}
int f[n+1]={0};
int ans=0;
for(int i=1;i<n;i++){
if(cel[1][i])
f[i+1]=1;
}
f[1]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
if((j+1>i-1||cel[j+1][i-1]==1)&&a[j]==a[i]&&f[j]>0)
f[i]=std::max(f[i],f[j]+1);
}
if(i==n||cel[i+1][n]) ans=std::max(ans,f[i]);
}
std::cout<<ans<<'n';
}
return 0;
}
os：怪，这个题卡memset
嘿嘿嘿，青啦青啦！
若有错误请指教，谢谢！
最后
以上就是认真冷风为你收集整理的Codeforces Round #804 (Div. 2)（A~D）的全部内容，希望文章能够帮你解决Codeforces Round #804 (Div. 2)（A~D）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复