文章目录
- 序言
- 题目一:古生物血缘远近判定
- 题目二:迷宫I
- 题目三:迷宫II
- 题目四:出界的路径数
- 题目五:最长公共字串
- 题目六:最长递增子序列
- 题目七:递增的三元子序列
- 题目八:最长回文字串
- 题目九:LT238. 除自身以外数组的乘积
- 题目十:分割数组
序言
汇总动态规划的题目 这部分可多了。
题目一:古生物血缘远近判定
DNA 是由 ACGT 四种核苷酸组成,例如 AAAGTCTGAC,假定自然环境下 DNA 发生异变的情况有:
基因缺失一个核苷酸
基因新增一个核苷酸
基因替换一个核苷酸
且发生概率相同
输入:ACT,AGCT
输出:1
思路是 组成一个矩阵,里面的数字都是0
| A | G | C | T | ||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| A | 0 | ||||
| C | 0 | ||||
| T | 0 |
如果上方字符和左边字符不一致的话,则可以做三种操作 即上面说的那三种情况。
那么我们将
左边格子+1 --> 代表一种情况 – 缺失一个核苷酸
上边格子 + 1 -->代表一种情况 – 新增一个核苷酸
左上方格子 + 1 -->代表 替换一个核苷酸
那如果上方字符和左边字符一致的话,则不需要替换 三个方位都不需要+1 ;不做任何改变。
最后当前格子是 这三个方位的最小值 。
所以,开始填满数字。
| A | G | C | T | ||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||
| A | 0 | 0 | 1 | 2 | 3 |
| C | 1 | 1 | 1 | 1 | 2 |
| T | 2 | 2 | 2 | 2 | 1 |
所以取最后一个格子就是1 就是答案。
import sys
str_lis = sys.stdin.readline().strip().split(',') #生成字符串列表
str1 = list(str_lis[0])
str1 = [str(_) for _ in str1]
str2 = list(str_lis[1])
str2 = [str(_) for _ in str2]
N1 = len(str1) #作为row 数
N2 = len(str2) #最为 col数
#创建一个dp网格
dp = [[0]*(N2+1) for _ in range(N1+1)]
for i in range(m+1):dp[i][0] = i
for j in range(n+1):dp[0][j] = j
#在表格填数字
for i in range(1,N1+1):
for j in range(1,N2+1):
if str1[i-1] == str2[j-1]:
p1 = dp[i-1][j-1]
else: p1 = dp[i-1][j-1] + 1
dp[i][j] = min(p1, dp[i-1][j], dp[i][j-1])
print(dp[N1][N2])
题目二:迷宫I
由空地(用 0 表示)和墙(用 1 表示)组成的迷宫 maze 中有一个球。球可以途经空地向 上、下、左、右 四个方向滚动,且在遇到墙壁前不会停止滚动。当球停下时,可以选择向下一个方向滚动。
给你一个大小为 m x n 的迷宫 maze ,以及球的初始位置 start 和目的地 destination ,其中 start = [startrow, startcol] 且 destination = [destinationrow, destinationcol] 。请你判断球能否在目的地停下:如果可以,返回 true ;否则,返回 false
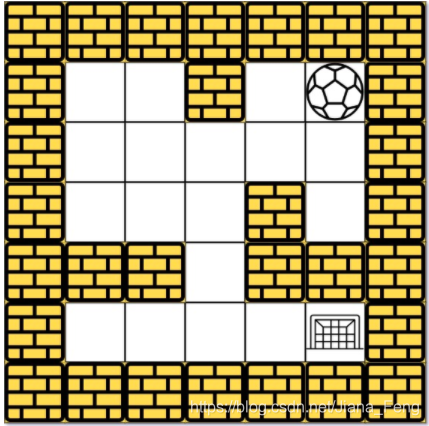
输入:maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
输出:true
输入:maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
输出:false
思路是:
先往前一步 看看是不是可以走的【即不超过长和宽 and maze[][]=0】
如果能走,继续往前探路,直到碰壁了 就要回到原来的位置 即退回原来的位置。
【同时要记得碰壁的时候,要记录下来这个位置 为true 表示曾经停留过】
def hasPath(maze, start, destination):
row = len(maze)
col = len(maze[0])
dire = ((1,0),(-1,0),(0,1),(0,-1))
stack = []
stack.append(start)
#创建dp记录停留过的痕迹
dp = [[False]*col for _ in range(row)]
dp[start[0]][start[1]]=True
while stack:
i,j = stack.pop(0)
if i,j==destination[0],destination[1]:return True
for di,dj in dire:
ni = i + di
nj = j + dj
while 0<= ni <row and 0<= nj <col and maze[ni][nj]==0:
ni += di
nj += dj
ni -= di
nj -= dj
if dp[ni][nj]:continue
else:
dp[ni][nj] =True
stack.append((ni,nj))
return False
题目三:迷宫II
题目505-迷宫:
由空地和墙组成的迷宫中有一个球。球可以向上下左右四个方向滚动,但在遇到墙壁前不会停止滚动。当球停下时,可以选择下一个方向。
给定球的起始位置,目的地和迷宫,找出让球停在目的地的最短距离。距离的定义是球从起始位置(不包括)到目的地(包括)经过的空地个数。如果球无法停在目的地,返回 -1。
这里迷宫的设定跟第一题差不多,但是这里要求返回的是找出让球停在目的地的最短距离。所以我们这次需要记录步数。
思路是: 怎么找到最短距离 如果有多条路线,如何定义哪条路是最短的。
这个时候dp网格记录是最短距离,如果两条路相撞 那么就要采用最短的步更新网格
首先是设置网格格子都是最大化 inf 这样好更新 不能设置为0,因为设置为就无法更新最短的步长。
def shortestDistance( maze, start, destination):
row,col = len(maze),len(maze[0])
stack = [start]
dp = [[float('inf')]*col for _ in range(row)]
dp[start[0]][start[1]] = 0
dire = ((1,0),(-1,0),(0,1),(0,-1))
while stack:
i,j = stack.pop(0)
for di,dj in dire:
ni = i + di
nj = j + dj
step = 1
while 0<= ni < row and 0 <= nj < col and maze[ni][nj]==0:
ni += di
nj += dj
step += 1
ni -= di
nj -= dj
step -= 1
if dp[i][j] + step < dp[ni][nj]:
dp[ni][nj] = dp[i][j] + step
stack.append((ni,nj))
if dp[destination[0]][destination[1]]==float('inf'):return -1
else: return dp[destination[0]][destination[1]]
题目四:出界的路径数
Leetcode题目–576:出界的路径数
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ,你可以将球移到相邻的单元格内,或者往上、下、左、右四个方向上移动使球穿过网格边界。但是,你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大,返回 结果 mod 109 + 7 的值
输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
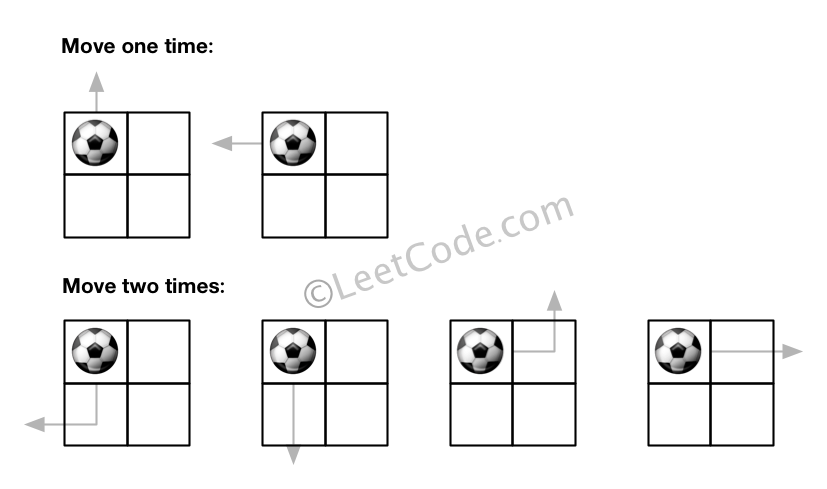
思路:肯定是动态规划,那么动态规划的核心是要找出状态与状态的关联性。
状态一:只移动一次就能出界,dp1每一个格子记录的是只移动一次能出界的走法
状态二:最多移动两次就能出界,那么dp2 = dp(只走一步) + dp(只走两步)
dp(只走两步) 可以看成 这个格子的上下左右的格子的dp(只走一步)
即
def findPaths( m, n, maxMove, startRow, startColumn):
dp = [[0]*col for _ in range(row)]
dire = ((0,-1),(0,1),(-1,0),(1,0))
for _ in range(maxMove):
cur = [[0]*col for _ in range(row)]
for di,dj in dire:
ni = startRow+di
nj = startColumn+dj
if 0>ni or ni >=row or 0>nj or nj >= col:
cur[ni][nj] += 1
else:
cur[ni][nj] = cur[ni][nj] + dp[ni][nj]
dp = cur
return dp[startRow][startColumn]
题目五:最长公共字串
给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。
输入:"1AB2345CD","12345EF"
输出:"2345"
思路是创建dp 来填数字,因为是字串 而不是子序列,所以需要按循序来。
即只有当两字符串字符相同的时候,才会有 dp[i][j] = dp[i-1][j-1] + 1
因为要输出 相应的字符,所以要定义 maxEnd 和maxLen,来记录
def LCS(str1 , str2 ):
m,n = len(str1),len(str2)
#创建表格dp
dp = [[0]*(n+1) for _ in range(m+1)]
maxLen , maxEnd = 0,0
for i in range(m):
for j in range(n):
if str1[i]==str2[j]:
dp[m+1][n+1] = dp[m][n] + 1
if dp[m+1][n+1]>maxLen:
maxLen = dp[m+1][n+1]
maxEnd = i
return str1[maxEnd-maxLen+1:maxEnd+1]
题目六:最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
这道题是一个维度的动态dp
首先要找到状态,定义状态,然后找到状态与状态的联系
假设例子为[10,9,2,5,3,7,101,18]
状态一:以10结尾的最长严格递增子序列长度是本身 1 ,因为前面没有元素
状态二:以9结尾的最长严格递增子序列长度是本身1,因为前面只有10,并不是递增
状态三:以2结尾的最长严格递增子序列长度是本身1,因为前面只有10,9,并不是递增
状态四:以5结尾的最长严格递增子序列长度是2,因为前面有比5小的数,是2
那么回去以2结尾的最长严格递增子序列长度是1,所以dp[5] = dp[2] + 1 =2
状态五:以3结尾的最长严格递增子序列长度是2,因为前面有比3小的数是2
那么回去以2结尾的最长严格递增子序列长度是1,所以dp[3] = dp[2] + 1 =2
状态六:以7结尾的最长严格递增子序列长度是3,因为前面有2,3,5
所以dp[7] = max(dp[2]+1, dp[3]+1, dp[5]+1) = max(2,3,3) = 3
状态七:以101结尾的最长严格递增子序列长度是4,因为前面有2,3,7
所以dp[101] = max(dp[2]+1, dp[3]+1, dp[7]+1,) = max(2, 3,4) = 4
状态八:以18结尾的最长严格递增子序列长度是4,因为前面有2,3,7
所以dp[18] = max(dp[2]+1, dp[3]+1, dp[7]+1,) = max(2, 3,4) = 4
所以我们现在找到状态与状态的联系了/
def lengthOfLIS(nums):
n = len(nums)
dp = [1]*n
for j in range(n):
for i in range(j):
if nums[j] > nums[i]:
dp[j] = max(dp[j], dp[i]+1)
return max(dp)
题目七:递增的三元子序列
给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。
如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则,返回 false 。
输入:nums = [1,2,3,4,5]
输出:true
解释:任何 i < j < k 的三元组都满足题意
输入:nums = [5,4,3,2,1]
输出:false
解释:不存在满足题意的三元组
输入:nums = [2,1,5,0,4,6]
输出:true
解释:三元组 (3, 4, 5) 满足题意,因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6
def lengthOfLIS(nums):
n = len(nums)
dp = [1]*n
for j in range(n):
for i in range(j):
if nums[j] > nums[i]:
dp[j] = max(dp[j], dp[i]+1)
return max(dp)>=3
题目八:最长回文字串
给你一个字符串 s,找到 s 中最长的回文子串。
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
输入:s = "cbbd"
输出:"bb"
输入:s = "a"
输出:"a"
思路是: 将s倒转,寻找公共的最长字串,但是我们还需要判断该字符串倒置前的下标和当前的字符串下标是不是匹配.
def longestPalindrome(self, s: str) -> str:
#创建一个矩阵
n = len(s)
dp = [[0]*(n+1) for _ in range(n+1)]
#两个数组rev_string = string[::-1]
s_rev = s[::-1]
maxLen = 0
maxEnd = 0
for i in range(n):
for j in range(n):
if s_rev[i] == s[j]:
dp[i+1][j+1] = dp[i][j] + 1
if dp[i+1][j+1] > maxLen and (n - 1 -i + dp[i+1][j+1]-1)== j:
maxLen = dp[i+1][j+1]
maxEnd = j
return s[maxEnd - maxLen + 1:maxEnd+1]
题目九:LT238. 除自身以外数组的乘积
输入: [1,2,3,4]
输出: [24,12,8,6]
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left = [0]*len(nums)
left[0]=1
for i in range(1,len(nums)):
left[i] = nums[i-1]*left[i-1]
right = [0]*len(nums)
right[len(nums)-1] = 1
for j in range(len(nums)-2,-1,-1):
right[j] = right[j+1]*nums[j+1]
ans = [0]*len(nums)
for i in range(len(nums)):
ans[i] = left[i] *right[i]
return ans
但这里的时间复杂度和空间复杂度是O(N)
题目十:分割数组
给定一个数组 A,将其划分为两个连续子数组 left 和 right, 使得:
left 中的每个元素都小于或等于 right 中的每个元素。
left 和 right 都是非空的。
left 的长度要尽可能小。
在完成这样的分组后返回 left 的长度。可以保证存在这样的划分方法
输入:[5,0,3,8,6]
输出:3
解释:left = [5,0,3],right = [8,6]
输入:[1,1,1,0,6,12]
输出:4
解释:left = [1,1,1,0],right = [6,12]
思路是:
左边区间的最大值要比右边区间的最小值都要小
所以
左边列表记录的是 在位置i切割的话,左边的最大值是多少
右边列表记录是 在位置i切割的话,右边的最小值是多少
举一例子是[5,0,3,8,6]
left : 5 5 5 8 8
right:0 0 3 6 6
有点错位,所以比较的时候要注意
得到left和right比较简单
那么决断点在哪呢?
当i=0的时候 比较 left[i] 和 right[i+1] 代表 在5那里切割 之后 比较左边的最大值和右边的最小值
所以切割点 是 当 left[i] <= right[i+1] 的时候,代表了 左边的最大值小于或等于 右边的最小值
def partitionDisjoint(self, nums: List[int]) -> int:
max_left,max_ = [],0
for num in nums:
max_ = max(max_, num)
max_left.append(max_)
min_right , min_ = [], float('inf')
for num in reversed(nums):
min_ = min(min_, num)
min_right = [min_] + min_right
for i in range(len(nums)-1):
if max_left[i] <= min_right[i+1]:
return i +1
最后
以上就是活力热狗最近收集整理的关于动态规划题目汇总的全部内容,更多相关动态规划题目汇总内容请搜索靠谱客的其他文章。
![[置顶] 【DP_背包专辑】【8、1最新更新】](https://www.shuijiaxian.com/files_image/reation/bcimg11.png)







发表评论 取消回复