微分流形基础点备注

【参考资料】
【1】《拓扑学的基础和方法》
【2】《物理学家用微分几何》
【3】《微分几何入门与广义相对论》

一、连续性

在拓扑空间中因为没有度量的概念，因此用开集的逆像仍然是开集来定义连续性，如下举例:

备注：拓扑里的开集、闭集可以理解是实数轴开区间、闭区间的推广。

二、流形

流形定义:可分的度量空间，并且它的任意点x都有领域同胚于n维开球
O B n = { x ∣ ρ ( 0 , x ) &lt; 1 } OB^n={x | rho(0, x) &lt; 1 } OBn={x∣ρ(0,x)<1}的拓扑空间，记作$M^n$

举例：

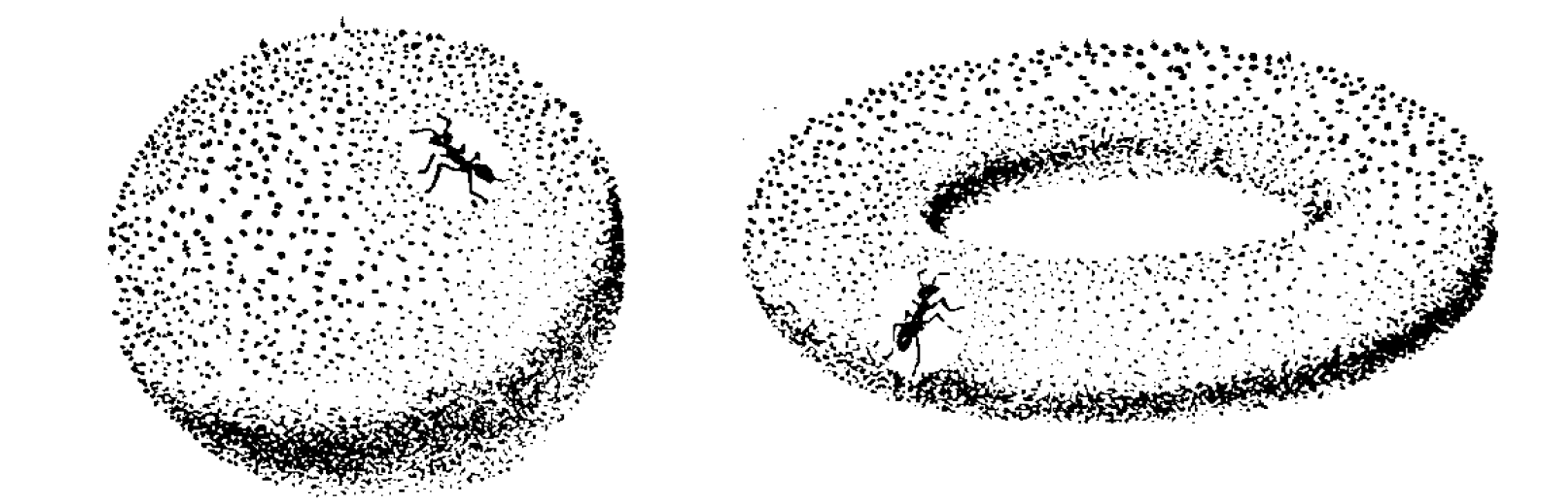
这里对于这只小蚂蚁而言，从它的视角看两者都是一个以当前点为圆心，半径为1的开圆的同胚

*另一种定义: 实（复）n维流形是一个豪斯道夫空间，它的每个点有开领域$R^n(C^n)$同胚。

注意:这里同胚的n值和n维流形的n值是一样的，比如一维直线是一维流形，但两条一维直线交叉就不是，因为交叉点明显不是一维的；二维的圆盘是二维流形，但三维的圆锥表面就不是，因为在圆锥的顶点是三维的，抛开这点的其他区域可以认为二维流形。可以将流形理解成一种高维空间的连续性。

三、微分流形

2.1 对微分的定义

有函数$y=f(x)$看做$f:R\to R$。做数列 { ( f ( x + h n ) − f ( x ) ) / h n } {(f(x + h_n) - f(x)) / h_n } {(f(x+hn​)−f(x))/hn​}，这里$h_n$是收敛于0的任意数列。因此当 { ( f ( x + h n ) − f ( x ) ) / h n } {(f(x + h_n) - f(x)) / h_n } {(f(x+hn​)−f(x))/hn​}与$h_n$无关的收敛到一个常数时，称f在x可微。
如果f在集合A上各个点可微，则称f在A上可微。

2.2 对坐标卡的定义

上图表示这样一个意思，在n维流形里有两个开集$U_{\alpha }$和$U_{\beta }$，它们分别存在到R^n的映射${\varphi }_{\alpha }$和${\varphi }_{\beta }$。

当流形M由若干个开集覆盖${\cup }_{\alpha }{U}_{\alpha }$，并且有对应的到$R^n$的映射，则我们有流形M的坐标卡集$A=(U_{\alpha },{\varphi }_{\alpha })$

2.3 对流形的微分结构定义

微分几何是研究微分流形在微分同胚变换下的不变性质。

备注：重申一下，可微（导）必然连续，但连续不一定可微（导）

前置定义1:考虑$f:R^n\to R$的情况，我们有偏导数$\frac{\partial f}{\partial x_i}$的定义。同时也可以对其他变量求导，因此有n阶偏导数的定义$\frac{{\partial }^{n}f}{\partial x_1\partial x_2...\partial x_n}$。当第n阶偏导数连续时，我们称f为$C^n$类函数。如果对于任意n都是成立的，则成为$C^{\infty }$类函数。

前置定义2: 回到"对坐标卡的定义"章节，我们还要求$(U_{\alpha },{\varphi }_{\alpha })$和$(U_{\beta },{\varphi }_{\beta })$满足相容条件:

$f={\varphi }_{\alpha }.{\varphi }_{\beta }^{\prime }:{\varphi }_{\alpha }(U_{\alpha }\cap U_{\beta })\to {\varphi }_{\beta }(U_{\alpha }\cap U_{\beta })$

备注：意味着定义了一个映射，从上图中$\alpha$对应的$R^n$（左边的阴影）映射到上图中$\beta$对应的$R^n$（右边的阴影）

这里的相容性要求这个映射f`$C^k$类函数，称两个坐标卡$C^k$相容

定义： 当流形M上的坐标卡集$A=(U_{\alpha },{\varphi }_{\alpha })$，满足如下三个条件，则称其为流形M的$C^k$微分结构:
(1) $U_{\alpha }$是流形M的开覆盖
(2) A中任意两个坐标卡都是$C^k$相容
(3) A为具备上述两个特性的最大的坐标卡集

当其相容为$C^{\infty }$时成为光滑流形。

举例(重要):

我们已知球面是一个二维流形，定义如下:
S 2 = { ( x , y , z ) ∈ R ∣ x 2 + y 2 + z 2 = 1 } S^2={(x,y,z)in R|x^2 + y^2 + z^2 = 1} S2={(x,y,z)∈R∣x2+y2+z2=1}
可以取两个开集
U + = { ( x , y , z ) ∈ S 2 ; z ≠ − 1 } U_{+}={(x,y,z) in S^2 ; z ne -1} U+​={(x,y,z)∈S2;z̸​=−1}，即整个球面去掉-1定点
U − = { ( x , y , z ) ∈ S 2 ; z ≠ 1 } U_{-}={(x,y,z) in S^2 ; z ne 1} U−​={(x,y,z)∈S2;z̸​=1}，即整个球面去掉+1定点

分别定义两个微分结构:
备注: 其实就是定义一个从M到$R^2$的映射
${\varphi }_{+}:(x,y,z)\to (\frac{x}{1+z},\frac{y}{1+z})$
${\varphi }_{-}:(x,y,z)\to (\frac{x}{1-z},\frac{y}{1-z})$
这个映射在几何上就是从定点z=1或-1做(x,y)的投影映射，映射到z=0的平面上。 可以证明他们是$C^{\infty }$相容的，因此$S^2$是二维光滑流形。

最后

以上就是友好硬币为你收集整理的微分流形基础点备注的全部内容，希望文章能够帮你解决微分流形基础点备注所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。