【蓝桥杯】 2018年国赛 矩阵求和

题目

题目：

经过重重笔试面试的考验，小明成功进入 Macrohard 公司工作。
今天小明的任务是填满这么一张表：
表有 n 行 n 列，行和列的编号都从1算起。
其中第 i 行第 j 个元素的值是 gcd(i, j)的平方，
gcd 表示最大公约数，以下是这个表的前四行的前四列：
1 1 1 1
1 4 1 4
1 1 9 1
1 4 1 16

小明突然冒出一个奇怪的想法，他想知道这张表中所有元素的和。
由于表过于庞大，他希望借助计算机的力量。

题解：

已知可以用欧拉函数和莫比乌斯反演来做
题目其实就是问

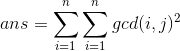
欧拉函数：

莫比乌斯反演：

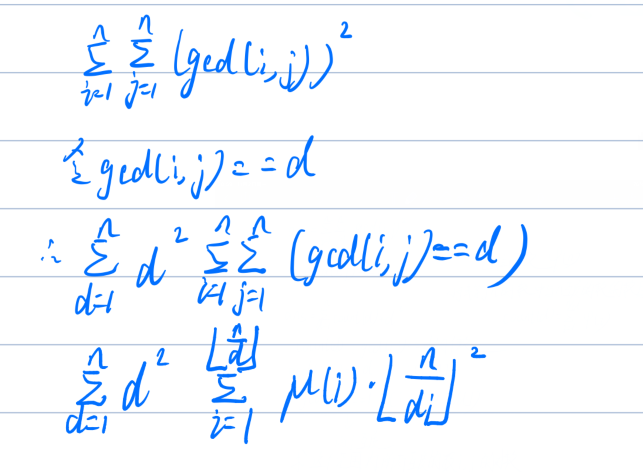
代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+9;
typedef long long ll;
bool vis[maxn];
ll prime[maxn];
ll phi[maxn];
ll s[maxn];

const int mod=1e9+7;
void Euler(int n)
{
	phi[1]=1;
	int cnt=0;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			prime[cnt++]=i;
			phi[i]=i-1;
		}
		for(int j=0;j<cnt&&i*prime[j]<=n;j++)
		{
			vis[prime[j]*i]=1;
			if(i%prime[j])
			{
				phi[i*prime[j]]=phi[i]*(prime[j]-1);
			}
			else 
			{
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
		 } 
	}
	s[1]=phi[1];
	for(int i=2;i<n;i++)
	{
		s[i]=s[i-1]+2*phi[i];
	}
}
int main()
{
	int n;
	Euler(maxn);
	ll sum=0;
	while(cin>>n)
	{
		sum=0;
		for(ll i=1;i<=n;i++)
		sum=(sum+s[n/i]%mod*i%mod*i%mod)%mod;
		cout<<sum<<endl;
	}
}

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int mod=1e9+7;
const int maxn = 10000000 + 10;
ll mu[maxn], vis[maxn], prim[maxn];
ll cnt = 0;		//素数的个数
ll d[maxn];
ll sum(int n)
{
	ll ans=0;
	for(int l=1,r;l<=n;l=r+1)		//整除分块 
	{
		r=n/(n/l);
		ans=(ans+(mu[r]-mu[l-1]+mod)%mod*((ll)n/l)%mod*((ll)n/l)%mod)%mod;
	}
	return ans;
}
void get_mu(int n)
{
	mu[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		if (!vis[i]) { prim[++cnt] = i; mu[i] = -1; }
		for (int j = 1; j <= cnt && prim[j] * i <= n; j++)
		{
			vis[prim[j] * i] = 1;
			if (i%prim[j] == 0)break;
			else mu[i*prim[j]] = -mu[i];
		}
	}
	for(int i=1;i<=n;i++)
	{
		d[i]=((ll)i*i)%mod;
	}
	for(int i=2;i<=n;i++)
	{
		d[i]=(d[i-1]+d[i])%mod;			//d的前缀和 
		mu[i]=(mu[i-1]+mu[i]+mod)%mod;	//mu的前缀和 
	}
	ll ans=0;
	for(int l=1,r;l<=n;l=r+1)			//整除分块 
	{
		r=n/(n/l);
		ans=(ans+(ll)(d[r]-d[l-1]+mod)%mod*(ll)sum(n/l)%mod)%mod;
	}
	cout<<ans<<endl;
}
int main()
{
	int n;
	cin>>n;
	get_mu(n);
	return 0;
}

最后

以上就是含蓄香水为你收集整理的【蓝桥杯】 2018年国赛 矩阵求和的全部内容，希望文章能够帮你解决【蓝桥杯】 2018年国赛 矩阵求和所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。