因果效应,典型模型及wasserstein距离, BNN,CFR,SITE,NetDeconfCFR_netwasserstein 距离参考

CFR_net

网络结构

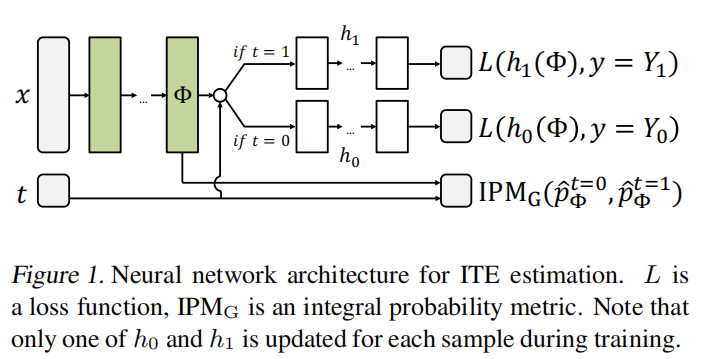
目标函数

设计思想

$$Loss={ϵ}_F+reg\_Loss+{ϵ}_{CF}\text{\hspace{1em}(1)}$$
由如下推导可知其$IMP(\Phi (x))$ 决定了 counterfactual loss 的上界, 即 upper error bound.

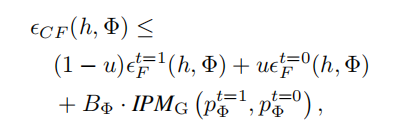
于是, 可得整体的目标函数为:

balanced learning

由于混淆变量导致的样本分布不均是因果效应预估的重大挑战. 那么该任务的关键就是在特征的表示空间上学到一个均衡的分布.

wasserstein 距离

用于衡量两个分布之间的差异, 具体地, 它描述了由一个分布转变为另一个分布所需要的最小代价.

离散直观举例

该问题来源于 optimal transport 最优传输问题, 一个直观的例子见下.
有一批石子分布在n个发货地址, 需要运送到m个有需求的收货地址. 令运输代价=运输数量 * 运输距离.

• 发货地址的石子分布为$p(1),...,p(n)$; 收货地址的石子分布为$q(1),...,q(m)$, 总的供需平衡;
• $dist(i,j)$表示两个地址之间的距离;
• $num(i,j)$ 表示某种运输方案T下, 从i地到j地运输的石子数量.
  那么该方案下的代价 为
  $$cost(p,q,t)=\sum _j^m\sum _i^{n}dist(i,j)\times num(i,j)$$.
  不同的方案有不同的代价, wasserstein 距离就是其中最小的代价.
  $$wass(p,q)=min\sum _j^m\sum _i^{n}dist(i,j)\times num(i,j)$$

连续数学抽象

该定义来自参考[5]
$\Omega$ 是一个任意空间, D 是该空间的一个距离度量, $\mu (x),\nu (x)$是点x在该空间的两个概率密度函数.
wasserstein distance定义为:
$$wass(\mu ,\nu )=\underset{\pi \in \prod (\mu ,\nu )}{\inf }{\int }_{{\Omega }^2}D(x,y)d\pi (\mu ,\nu )$$
where $\prod (\mu ,\nu )$ 是联合概率分布. 其两个边缘概率分布可表示为
${\int }_{\nu }\pi (\mu ,\nu )=\mu$, ${\int }_{\mu }\pi (\mu ,\nu )=\nu$.
符号 inf 为infimum, 表示下确界, 可简单理解为 min.

距离求解的代码实现

由 wasserstein 距离 的定义可知, 它不像向量距离这样是一个现成的闭式解表达式, 而是一个最优化问题. 求解涉及到 dual 对偶转换, 且有较大的计算复杂度.
在 python中, tensorflow 中怎么近似快速计算 wasserstein 距离, 参考[2,4]的附录代码中均给出了同样的实现, 它的实现又是来自参考[5].

与KL散度的关系

通常机器学习的多分类任务中会涉及到 交叉熵, 它等于KL散度减去一个固定的值. 但KL散度不满足距离的定义.

参考

1. BNN, ICML2016
2. CFR_net,ICML 2017, paper, code
3. SITE,NeuralIPS 2018
4. NetDeconf,WSDM2020, paper, code
5. ICML2014,Fast Computation of Wasserstein Barycenters

最后

以上就是粗暴发夹为你收集整理的因果效应,典型模型及wasserstein距离, BNN,CFR,SITE,NetDeconfCFR_netwasserstein 距离参考的全部内容，希望文章能够帮你解决因果效应,典型模型及wasserstein距离, BNN,CFR,SITE,NetDeconfCFR_netwasserstein 距离参考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。