0 参考资料
[1] 智能优化算法及其MATLAB实例(第2版),包子阳等.
链接: https://pan.baidu.com/s/1hXGvsEJfP4nBFpkaQ-zxIA 提取码: j9qb
[2] 计算智能,张军等.
链接: https://pan.baidu.com/s/1ahstyLP-vP7Y_r0gbbQx0A 提取码: nf3t
[3] python用禁忌搜索算法实现TSP旅行商问题_小白-CSDN博客
[4] 禁忌搜索算法的实现_Python_ttphoon的博客-CSDN博客_禁忌搜索算法python
1 禁忌搜索算法简介
禁忌搜索算法(Tabu Search Algotithm, TSA)的思想最早由美国工程院院士Glover教授于1986年提出,并在1989年和1990年对该方法做出了进一步的定义和发展。
所谓禁忌,就是禁止重复前面的操作。为了改进局部邻域搜索容易陷入局部最优点的不足,禁忌搜索算法引入一个禁忌表,记录下已经搜索过潜在最优解,在下一次搜索中,对禁忌表中的信息不再搜索或有选择地搜索,以此来跳出局部最优点,从而最终实现全局优化。禁忌搜索算法是对局部邻域搜索的一种扩展,是一种全局邻域搜索、逐步寻优的算法。
禁忌搜索算法是一种迭代搜索算法,它区别于其他现代启发式算法的显著特点是利用记忆来引导算法的搜索过程;它是对人类智力过程的一种模拟,是人工智能的一种体现。禁忌搜索算法涉及邻域、禁忌表、禁忌长度、候选解、藐视准则等概念,在邻域搜索的基础上,通过禁忌准则来避免重复搜索,并通过藐视准则来赦免一些被禁忌的优良状态,进而保证多样化的有效搜索来最终实现全局优化。
在自然计算的研究领域中,禁忌搜索算法以其灵活的存储结构和相应的禁忌准则来避免迂回搜索,在智能算法中独树一帜,成为一个研究热点,受到了国内外学者的广泛关注。迄今为止,禁忌搜索算法在组合优化、生产调度、机器学习、电路设计和神经网络等领域取得了很大的成功,近年来又在函数全局优化方面得到较多的研究,并有迅速发展的趋势。
2 禁忌搜索算法理论
禁忌搜索算法是模拟人的思维的一种智能搜索算法,即人们对已搜索的地方不会再立即去搜索,而是先去对其他地方进行搜索,若没有找到,可再搜索已去过的地方。
禁忌搜索算法从一个初始可行解出发,以特定的方法选择领域后,在领域内寻求最优解(局部最优解)。为了避免陷入局部最优解,禁忌搜索中采用了一种灵活的“记忆”技术,即对已经进行的优化过程进行记录,指导下一步的搜索方向,这就是禁忌表的建立方式。禁忌表中保存了最近若干次迭代过程中领域内的局部最优解,凡是处于禁忌表中的解,在当前迭代过程中都是禁忌进行的,这样可以避免算法重新访问在最近若干次迭代过程中已经访问过的解,从而防止了循环,帮助算法摆脱局部最优解。另外,为了尽可能不错过产生最优解的“移动”,禁忌搜索还采用藐视准则的策略,以特定的规则释放禁忌表中某些能改善当前最优解的禁忌解。
3 禁忌搜索算法的特点
禁忌搜索算法是在邻域搜索的基础上,通过设置禁忌表来禁忌一些已经进行过的操作,并利用藐视准则来特赦一些优良状态。
与传统的优化算法相比,禁忌搜索算法的主要特点是:
- 禁忌搜索算法的初始解的选择:可能不是在当前解的邻域中随机产生,它要么是但禁忌表和可行解都不为空时造成最优目标值的解(禁忌解);要么是当所有可行解都被禁忌后,禁忌表中的最佳解;要么是禁忌表为空时,可行解中的最佳解。因此选取优良解的概率远远大于其他劣质解的概率。
- 禁忌搜索算法最佳状态选择的选择:并不是每一轮迭代都会更新当前最佳状态,只有当禁忌表中的禁忌解或者可行解导致的状态优于当前最优解时才会导致当前最优解的更新。
由于禁忌搜索算法具有灵活的记忆功能和藐视准则,并且在搜索过程中可以接受劣质解,所以具有较强的“爬山”能力,搜索时能够跳出局部最优解,转向解空间的其他区域,从而增大获得更好的全局最优解的概率。因此,禁忌搜索算法是一种局部搜索能力很强的全局迭代寻优算法。
4 禁忌搜索算法的改进
禁忌搜索是著名的启发式搜索算法,但是禁忌搜索也有明显的不足,即在以下方面需要改进:
- 对初始解有较强的依赖性,好的初始解可使禁忌搜索算法在解空间中搜索到好的解,而较差的初始解则会降低禁忌搜索的收敛速度。因此可以与遗传算法、模拟退火算法等优化算法结合,先产生较好的初始解,再用禁忌搜索算法进行搜索优化。
- 迭代搜索过程是串行的,仅是单一状态的移动,而非并行搜索。为了进一步改善禁忌搜索的性能,一方面可以对禁忌搜索算法本身的操作和参数选取进行改进,对算法的初始化、参数设置等方面实施并行策略,得到各种不同类型的并行禁忌搜索算法;另一方面则可以与遗传算法、神经网络算法以及基于问题信息的局部搜索相结合。
- 在集中性与多样性搜索并重的情况下,多样性不足。集中性搜索策略用于加强对当前搜索的优良解的邻域做进一步更为充分的搜索,以期找到全局最优解。多样性搜索策略则用于拓宽搜索区域,尤其是未知区域,当搜索陷入局部最优时,多样性搜索可改变搜索方向,跳出局部最优,从而实现全局最优。增加多样性策略的简单处理手段是对算法的重新随机初始化,或者根据频率信息对一些已知对象进行惩罚。
5 禁忌搜索的算法流程
禁忌搜索算法的基本思想是:对一个以某种方法获得的初始解,在一种邻域范围内对其进行一系列变化,从而得到许多候选解;从这些候选解中选出最优候选解,再将此最优解导致的最优状态与被禁忌的解导致的最优状态比较,以选出最优解,并将该解作为新的初始解,最后将其加入禁忌表(如果是禁忌解则更新禁忌期限);然后将此最优解对应的状态与当前最优解状态进行比较,若其优于当前最优状态,就选择该状态作为新的当前最优状态;如果所有的解都被禁忌,则直接选择禁忌解中的最佳值作为新的初始解,选定新的初始解后再更新禁忌表,并判断是否更新最优状态;如果禁忌表为空时直接取可行解中的最优值作为新的初始解,选定新的初始解后再更新禁忌表,并判定是否更新最优状态。重复上述过程,直到满足停止准则。其算法步骤如下:
- 给定禁忌搜索算法参数,随机产生初始解x,置禁忌表为空;
- 利用初始解(新的初始解)的邻域函数产生其所有(或若干)邻域解,并从中确定若干候选解,在禁忌表中的;
- 从这些候选解中选出最优候选解,再将此最优解导致的最优状态与被禁忌的解导致的最优状态比较以选出最优解,并将该解作为新的初始解,最后将其加入禁忌表(如果是禁忌解则更新禁忌期限)
- 如果所有的解都被禁忌,则直接选择禁忌解中的最佳值作为新的初始解,选定新的初始解后再更新禁忌表;
- 如果禁忌表为空时直接取可行解中的最优值作为新的初始解,选定新的初始解后再更新禁忌表;
- 将此最优解对应的状态与当前最优解状态进行比较,若其优于当前最优状态,就选择该状态作为新的当前最优状态;
- 判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则,转步骤(2)。
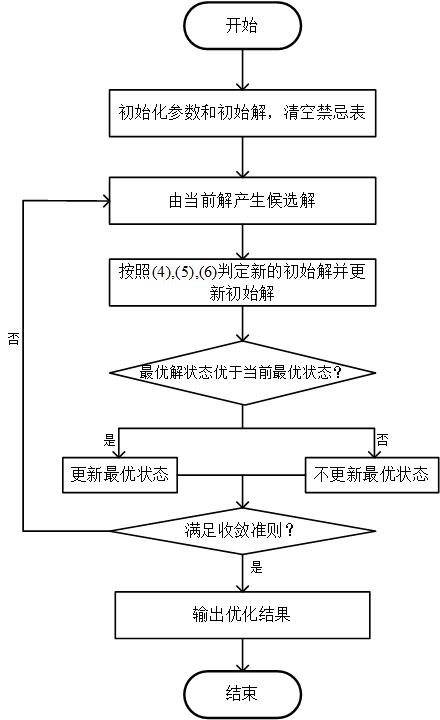
禁忌搜索算法的运算流程如图5.1所示。
|
|
| 图5.1 禁忌搜索算法流程图 |
6 禁忌搜索算法基本要素说明
初始解、适配值函数、邻域结构、候选解的选择、禁忌期限、禁忌对象、藐视准则、终止准则等是影响禁忌搜索算法性能的关键。邻域函数沿用局部邻域搜索的思想,用于实现邻域搜索;禁忌表和禁忌对象的设置,体现了算法避免迂回搜索的特点;藐视准则,则是对优良状态的奖励,它是对禁忌策略的一种放松。
6.1基本参数说明
(1)初始解
禁忌搜索算法可以随机给出初始解,也可以事先使用其他算法或者启发式算法等给出一个较好的初始解。
由于禁忌搜索算法主要是基于邻域搜索的,初始解的好坏对搜索的性能影响很大。尤其是一些带有很复杂约束的优化问题,如果随机给出的初始解很差,甚至通过多步搜索也很难找到一个可行解,这时应该针对特定的复杂约束,采用启发式方法或其他方法找出一个可行解作为初始解;再用禁忌搜索算法求解,以提高搜索的质量和效率。
(2)禁忌对象
所谓禁忌对象,就是被置入禁忌表中的那些变化元素。禁忌的目的则是为了尽量避免迂回搜索而多搜索一些解空间中的其他地方。归纳而言,禁忌对象通常可选取状态本身或状态分量等。
(3)禁忌表
不允许恢复(即被禁止)的性质称作禁忌(Tabu)。禁忌表的主要目的是阻止搜索过程中出现循环和避免陷入局部最优,它通常记录前若干次的移动,禁止这些移动在近期内返回。在迭代固定次数后,禁忌表释放这些移动,重新参加运算,因此它是一个循环表,每迭代一次,就将最近的一次移动放在禁忌表的末端,而它的最早的一个移动就从禁忌表中释放出来。
(4)禁忌期限
所谓禁忌长度,或禁忌期限,是指禁忌对象在不考虑特赦准则的情况下不允许被选取的最大次数。通俗地讲,禁忌长度可视为禁忌对象在禁忌表中的任期。禁忌对象只有当其任期为0时才能被解禁。在算法的设计和构造过程中,一般要求计算量和存储量尽量小,这就要求禁忌长度尽量小。但是,禁忌长度过小将造成搜索的循环。禁忌长度的选取与问题特征相关,它在很大程度上决定了算法的计算复杂性。
一方面,禁忌长度可以是一个固定常数,或者固定为与问题规模相关的一个量;另一方面,禁忌长度也可以是动态变化的,如根据搜索性能和问题特征设定禁忌长度的变化区间,而禁忌长度则可按某种规则或公式在这个区间内变化。
6.2基本准则说明
(1)适配值函数
禁忌搜索的适配值函数用于对搜索进行评价,进而结合禁忌准则和藐视准则来选取新的当前状态。
目标函数值和它的任何变形都可以作为适配值函数。若目标函数的计算比较困难或耗时较长,此时可采用反映问题目标的某些特征值来作为适配值,进而改善算法的时间性能。选取何种特征值要视具体问题而定,但必须保证特征值的最佳性与目标函数的最优性一致。适配值函数的选择主要考虑提高算法的效率、便于搜索的进行等因素。
(2)邻域搜索准则
所谓邻域结构,是指从一个解(当前解)通过“移动”产生另一个解(新解)的途径,它是保证搜索产生优良解和影响算法搜索速度的重要因素之一。
通过移动,目标函数值将产生变化,移动前后的目标函数值之差,称之为移动值。如果移动值是非负的,则称此移动为改进移动;否则称之为非改进移动。最好的移动不一定是改进移动,也可能是非改进移动,这一点能保证在搜索陷入局部最优时,禁忌搜索算法能自动把它跳出局部最优。邻域结构的设计通常与问题相关。邻域结构的设计方法很多,对不同的问题应采用不同的设计方法,常用设计方法包括互换、插值、逆序等。不同的“移动”方式将导致邻域解个数及其变化情况的不同,对搜索质量和效率有一定影响。
(3)藐视准则
在禁忌搜索算法中,可能会出现候选解全部被禁忌,或者存在一个优于当前最优状态的禁忌候选解,此时藐视准则将某些状态解禁,以实现更高效的优化性能。特赦准则的常用方式有:
- 基于适配值的原则:某个禁忌候选解的适配值优于当前最优状态,则解禁此候选解为当前状态和新的初始解。
- 基于搜索方向的准则:若禁忌对象上次被禁忌时使得适配值有所改善,并且目前该禁忌对象对应的候选解的适配值优于当前解,则对该禁忌对象解禁。
(4)搜索策略
搜索分为集中性搜索策略和多样性搜索策略。集中性搜索策略用于加强对优良解的邻域的进一步搜索。其简单的处理手段可以是在一定步数的迭代后基于最佳状态重新进行初始化,并对其邻域进行再次搜索。在大多数情况下,重新初始化后的邻域空间与上一次的邻域空间是不一样的,当然也就有一部分邻域空间可能是重叠的。
多样性搜索策略则用于拓宽搜索区域,尤其是未知区域。其简单的处理手段可以是对算法的重新随机初始化,或者根据频率信息对一些己知对象进行惩罚。
(5)候选解选择
候选解通常在当前状态的邻域中择优选取,若选取过多将造成较大的计算量,而选取较少则容易“早熟”收敛,但要做到整个邻域的择优往往需要大量的计算,因此可以确定性地或随机性地在部分邻域中选取候选解,具体数据大小则可视问题特征和对算法的要求而定。
(6)终止准则
禁忌搜索算法需要一个终止准则来结束算法的搜索进程,而严格理论意义上的收敛条件,即在禁忌长度充分大的条件下实现状态空间的遍历,这显然是不可能实现的。因此,在实际设计算法时通常采用近似的收敛准则。
常用的方法有:
- 给定最大迭代步数。当禁忌搜索算法运行到指定的迭代步数之后,则终止搜索;
- 设定某个对象的最大禁忌频率。若某个状态、适配值或对换等对象的禁忌频率超过某一阈值,或最佳适配值连续若干步保持不变,则终止算法;
- 设定适配值的偏离阈值。首先估计问题的下界,一旦算法中最佳适配值与下界的偏离值小于某规定阈值,则终止搜索。
7 禁忌搜索算法解决TSP问题的Python代码实现
本代码提供了两种初始化方法:随机产生初始解以及贪心算法产生初始解。代码主要是在'python用禁忌搜索算法实现TSP旅行商问题_小白-CSDN博客'的基础上进行修改的,在原代码使用贪心算法获取初始解的基础上增加了随机得到一组初始解的方法;对更新当前最优值的方法以及获取新初始解的方法做了一些改进,改进方法即为本文第五节所示;然后对结果可视化部分做了改进,增加了迭代曲线以及动图展示部分;对一些关键参数,比如禁忌期限,领域结构做了调整;最后还添加了详尽的注释,希望能节约大家阅读代码的时间。
此外,本文使用的数据来源于'禁忌搜索算法的实现_Python_ttphoon的博客-CSDN博客_禁忌搜索算法python',没有使用‘python用禁忌搜索算法实现TSP旅行商问题_小白-CSDN博客’的数据。
import random
import matplotlib.pyplot as plt
import sys
import copy
import numpy as np
import matplotlib.animation as animation
'''
TSA的核心在于藐视规则的设置,禁忌表的更新
'''
# 初始三十个城市坐标
city_x = [
1150, 630, 40, 750, 750, 1030, 1650, 1490, 790, 710, 840, 1170, 970, 510,
750, 1280, 230, 460, 1040, 590, 830, 490, 1840, 1260, 1280, 490, 1460,
1260, 360
]
city_y = [
1760, 1660, 2090, 1100, 2030, 2070, 650, 1630, 2260, 1310, 550, 2300, 1340,
700, 900, 1200, 590, 860, 950, 1390, 1770, 500, 1240, 1500, 790, 2130,
1420, 1910, 1980
]
# 城市数量
n = 29
# [ [ 5 for col in range(3)] for raw in range(4)] 生成3*4阶矩阵的方法,矩阵中所有元素均为5
distance = [[0 for col in range(n)]
for raw in range(n)] # 生成一个29*29的全0矩阵,存放distance
# 禁忌表
tabu_list = []
tabu_time_count = []
# 领域容量(领域的选择个数)
neighbor_capacity = 50 # 不能太大,否则陷入死循环;也不能太小,不然全局搜索能力太差
# 当前禁忌对象数量
current_tabu_num = 0
# 禁忌期限(元素在禁忌表中待的时间)
tabu_tenure = 50
# 候选集
candidate = [[0 for col in range(n)]
for raw in range(neighbor_capacity)] # 50*29阶矩阵
candidate_distance = [sys.maxsize for subset in range(neighbor_capacity)
] # 生成50个元素的一维矩阵存放候选距离
tabu_candidate_distance = copy.copy(candidate_distance) # 存储禁忌表中路径的距离,以使用藐视规则
# 最佳路径以及最佳距离
best_route = []
best_distance = sys.maxsize # sys.maxsize返回系统能存储的最大整数值(9223372036854775807)
current_route = []
current_distance = 0.0
# 构建初始参考距离矩阵,矩阵的每一行都是一个城市到其余城市的距离
def getdistance():
for i in range(n):
for j in range(n):
x = pow(city_x[i] - city_x[j], 2)
y = pow(city_y[i] - city_y[j], 2)
distance[i][j] = pow(x + y, 0.5)
for i in range(n):
for j in range(n):
if distance[i][j] == 0:
distance[i][j] = sys.maxsize # 设置出发点到自身的距离为无穷大
def initial_solution_greedy(): # 初始解求解函数1——贪婪算法
# 通过贪婪算法确定初始解,初始解并不是随机获取的,而是选择第一个城市的最近的城市,依次类推
sum = 0.0
# 必须实例化一个一个赋值,或者使用deepcopy赋值不然只是把地址赋值
dis = copy.deepcopy(distance)
visited = [] # 记录走过的城市
# 进行贪婪选择——每次都选择距离最近的城市
id = 0 # 出发城市到其余城市的距离的编号
for i in range(n):
for j in range(n): # j为出发城市编号
dis[j][
id] = sys.maxsize # 从某个城市出发后便不能再回到该城市,所有行与该城市的距离设置为无穷大,假设从题目的第一个城市出发
minvalue = min(dis[id]) # 找到该城市最近的城市
if i != n - 1:
sum += minvalue
visited.append(id)
id = dis[id].index(
minvalue) # 转移到选择的第二个city,上个城市与其余城市最小距离的索引设置为id,再到第id行去找最小距离
return visited
def initial_solution_random(): # 初始解求解函数2——随机算法
id = [x for x in range(0, n)]
random.shuffle(id) # shuffle返回空,不要使用直接赋值
visited = copy.copy(id)
return visited
# 计算总距离(藐视准则函数,适配函数、目标函数)
def cacl_distance(rho): # rho是一个从第一个城市出发指向下一个城市(通过贪心算法或者随机选择的)的数组
sumdis = 0.0
for i in range(n - 1):
sumdis += distance[rho[i]][rho[i + 1]]
sumdis += distance[rho[0]][rho[-1]] # 回到最初的城市
return sumdis
# 初始设置(初始赋值,只执行一次)
def initial_set(method):
global best_route
global best_distance
global tabu_time_count
global current_tabu_num
global current_distance
global current_route
global tabu_list
# 得到初始解以及初始距离
if (method == 1):
current_route = initial_solution_greedy() # 返回初始路径
elif (method == 2):
current_route = initial_solution_random()
best_route = copy.copy(current_route) # 以当前路径作为最优路径
# =为赋值,原新列表通过append改变时同时影响新旧列表,地址一样,最好不要使用赋值语句来复制数组;
# 特别地,如果对原或新列表再次赋值,则会重新分配地址,互不影响;
# copy为浅拷贝,原新列表外层通过append改变时不影响copy列表,但影响=列表,新旧列表地址不同;
# deepcopy为深层拷贝,原新列表内层通过append改变时影响copy(地址不同但会影响)和=列表但不影响deepcopy列表,新旧列表地址不同。
current_distance = cacl_distance(current_route)
best_distance = current_distance # 以当前距离作为最优距离
# 置禁忌表为空
tabu_list.clear()
tabu_time_count.clear()
current_tabu_num = 0
# 交换数组两个元素,通过交换的方式获取邻域,返回交换两个元素后的新列表
def exchange(index1, index2, arr): # index为需要交换的两个元素,arr为需要交换的数组
current_list = copy.copy(arr)
current = current_list[index1]
current_list[index1] = current_list[index2]
current_list[index2] = current
return current_list
# 得到邻域 候选解
def candidate_best_path(): # 通过任意交换两个城市来获取领域
global best_route
global best_distance
global current_tabu_num
global current_distance
global current_route
global tabu_list
# 存储两个交换的位置
exchange_position = []
candidate = [[0 for col in range(n)]
for raw in range(neighbor_capacity)] # 50*29阶矩阵
candidate_distance = [sys.maxsize for subset in range(neighbor_capacity)
] # 生成50个元素的一维矩阵存放候选距离,邻域的容量为50
tabu_candidate_distance = copy.copy(
candidate_distance) # 存储禁忌表中路径的距离,以使用藐视规则
temp = 0
mark_candidate_distance = 0
mark_tabu_candidate_distance = 0
# 随机选取邻域
while True:
current = random.sample(range(0, n), 2) # 0到n-1中随机选择2个数存储在数组current中
if current not in exchange_position:
exchange_position.append(current)
candidate[temp] = exchange(
current[0], current[1], current_route
) # exchange函数返回交换两个元素之后的路径列表,current_route由贪心或者随机算法确定
if candidate[temp] not in tabu_list: # 排除被禁忌的邻域
candidate_distance[temp] = cacl_distance(
candidate[temp]) # 邻域的目标函数值
mark_candidate_distance = 1
else:
tabu_candidate_distance[temp] = cacl_distance(candidate[temp])
mark_tabu_candidate_distance = 1
temp += 1
if temp >= neighbor_capacity: # 50个邻域
break # 找齐200个邻域后退出while
# 按照以下规则选取最优路径
# 1.当禁忌表中的产生的最短距离、可行解的最短距离永远取最小者作为新的初始解;(此为藐视禁忌的规则)
# 2.最优距离在找到一个更小的距离后才会更新,哪怕是禁忌表中的解导致的最短距离;(此为最佳状态的确定规则)
# 特殊情况1: 禁忌表为空时直接选择可行解的最短距离作为初始解并按照2视情况决定是否更新当前最优解;
# 特殊情况2:可行解为空时直接选择禁忌表中的最小值作为新的可行解解并按照2视情况决定是否更新当前最优解
if (mark_candidate_distance == 1 and mark_tabu_candidate_distance
== 1): # 如果候选集合不为空集,取禁忌表中产生最短距离的禁忌解或者产生最短距离的可行解最小值作为新的初始解:
current_distance = min(candidate_distance)
tabu_best_candidate_distance = min(tabu_candidate_distance)
if (current_distance > tabu_best_candidate_distance):
may_best_distance = tabu_best_candidate_distance
best_index = tabu_candidate_distance.index(
tabu_best_candidate_distance)
else:
may_best_distance = current_distance
best_index = candidate_distance.index(current_distance)
if (best_distance >
may_best_distance): # 找到比当前最优小的距离就更新,哪怕是禁忌表中的解
best_distance = may_best_distance
best_route = candidate[best_index]
current_route = candidate[best_index]
elif (mark_tabu_candidate_distance == 0
): # 禁忌表中元素为空时不再考虑禁忌表,可行解最小距离小于当前最优则取可行解,否则不更新最优
best_index = candidate_distance.index(
min(candidate_distance)) # 不更新当前最优,但是需要更新初始解
if (min(candidate_distance) < best_distance):
best_distance = min(candidate_distance) # 候选最小作为最短路径距离
best_route = candidate[best_index]
current_route = candidate[best_index]
elif (mark_candidate_distance == 0
): # 如果所有候选解都被禁忌,寻求禁忌表中的最优解,不管是否大于当前最优并视情况决定是否更新当前最优解
tabu_best_candidate_distance = min(tabu_candidate_distance)
best_index = tabu_candidate_distance.index(best_distance)
current_route = candidate[best_index]
if (tabu_best_candidate_distance < best_distance):
best_distance = tabu_best_candidate_distance
best_route = candidate[best_index]
tabu_list.append(candidate[best_index]) # 将路径加入禁忌表
tabu_time_count.append(tabu_tenure)
current_tabu_num += 1 # 禁忌表中元素数量加1
# 更新禁忌表以及禁忌期限
def update_tabu():
global current_tabu_num
global tabu_time_count
global tabu_list
del_num = 0
temp = []
# 如果达到期限,释放
for i in range(current_tabu_num):
if tabu_time_count[i] == 0: # 判断是否有元素等于0
del_num += 1
temp = tabu_list[i] # 找到tabu_time_count中0在tabu.list对应的元素
current_tabu_num -= del_num # 删除元素后减少一个 current_tabu_num包含的元素数量
while 0 in tabu_time_count:
tabu_time_count.remove(0) # 移除计时器中的0
while temp in tabu_list:
tabu_list.remove(temp) # 移除禁忌表中计时器变为0的元素
# 更新步长
tabu_time_count = [x - 1 for x in tabu_time_count] # 所有元素都减去1
def draw():
global draw_best_distance
global bestx_every_t
global besty_every_t
global best_route
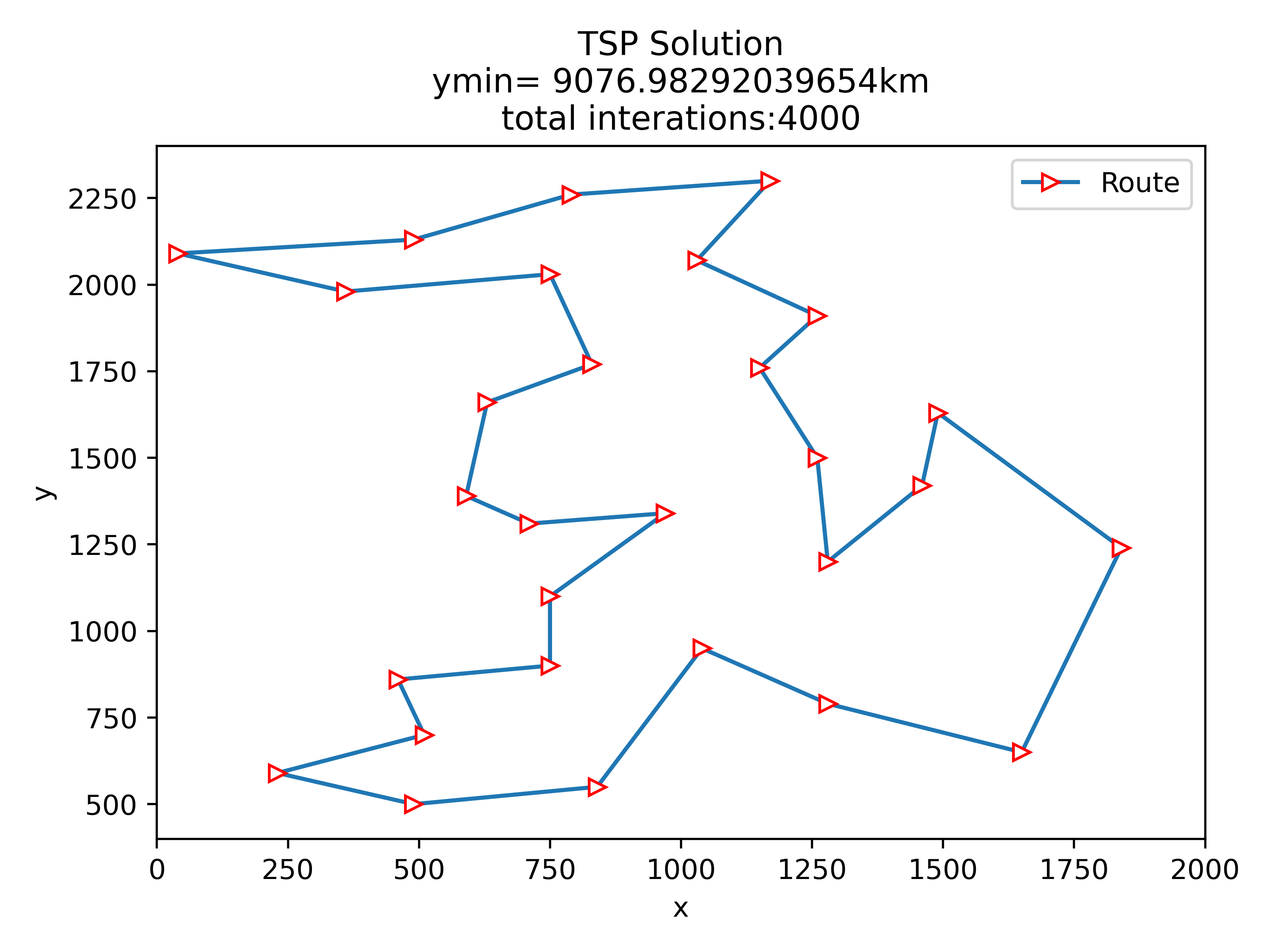
# 绘制最终结果图
result_x = [0 for col in range(n + 1)]
result_y = [0 for col in range(n + 1)]
best_distance = min(draw_best_distance)
index_final_best_distance = draw_best_distance.index(best_distance)
result_x = bestx_every_t[index_final_best_distance]
result_y = besty_every_t[index_final_best_distance]
plt.figure(tight_layout=True)
plt.xlim(0, 2000) # 限定横轴的范围
plt.ylim(400, 2400) # 限定纵轴的范围
plt.plot(result_x, result_y, marker='>', mec='r', mfc='w', label=u'Route')
plt.legend() # 让图例生效
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
plt.xlabel(u"x") # X轴标签
plt.ylabel(u"y") # Y轴标签
plt.title("TSP Solutionn" + 'ymin= {}'.format(best_distance) + 'km' +
'ntotal interations:' + str(len(bestx_every_t))) # 标题
plt.savefig('TS.1.png', dpi=500)
plt.pause(4)
plt.close()
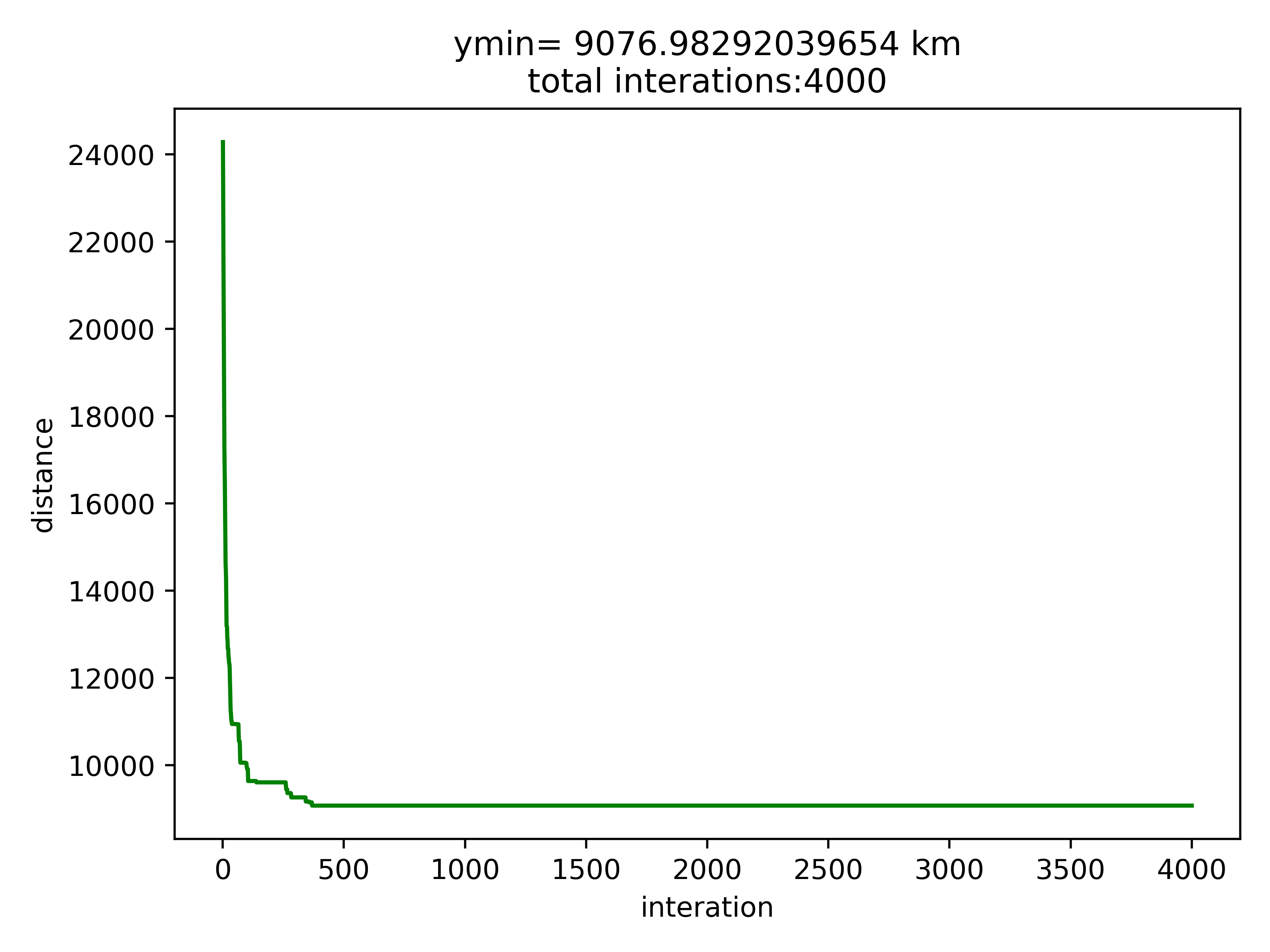
# 绘制迭代次数图
plt.figure(tight_layout=True)
x = range(1, len(draw_best_distance) + 1)
y = draw_best_distance
plt.plot(x, y, 'g-')
plt.title('ymin= {}'.format(best_distance) + ' km' +
'ntotal interations:' + str(len(bestx_every_t)))
plt.xlabel('interation')
plt.ylabel('distance')
plt.savefig('TS.2.png', dpi=500)
plt.pause(4)
plt.close()
# 绘制迭代动图
fig3 = plt.figure(tight_layout=True)
plt.xlim(0, 2000) # 限定横轴的范围
plt.ylim(400, 2400) # 限定纵轴的范围
line, = plt.plot(bestx_every_t[0],
besty_every_t[0],
marker='o',
mec='r',
mfc='w')
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
def update_scatter(num):
plt.title("TSP Solutionn" +
'ymin= {}'.format(draw_best_distance[num]) + ' km' +
'niter = ' + str((num + 1))) # 标题
line.set_data(bestx_every_t[num], besty_every_t[num])
return line,
ani = animation.FuncAnimation(
fig3,
update_scatter,
np.arange(0, len(bestx_every_t), int(0.02 * len(bestx_every_t))),
blit=True,
interval=100,
)
ani.save('TS.3.gif', writer='pillow')
draw_best_distance = []
bestx_every_t = [[0] * (len(city_y) + 1)]
besty_every_t = [[0] * (len(city_y) + 1)]
bestx_every_t = np.delete(bestx_every_t, 0, axis=0)
besty_every_t = np.delete(besty_every_t, 0, axis=0)
def solve():
global draw_best_distance
global bestx_every_t
global besty_every_t
global best_distance
getdistance()
runtime = int(input("迭代次数:"))
method = int(input('请输入初始化方法(1表示贪婪算法,2表示随机算法): '))
initial_set(method) # 获取初始解
for rt in range(runtime): # rt含义是在初始解基础上迭代次数
draw_result_x = []
draw_result_y = []
candidate_best_path() # 获取候选解等
for i in range(n):
draw_result_x.append(city_x[best_route[i]])
draw_result_y.append(city_y[best_route[i]])
draw_result_x.append(draw_result_x[0])
draw_result_y.append(draw_result_y[0])
bestx_every_t = np.vstack([bestx_every_t, draw_result_x])
besty_every_t = np.vstack([besty_every_t, draw_result_y])
draw_best_distance.append(best_distance)
update_tabu() # 更新禁忌表
print("最短距离:")
best_distance = str(min(draw_best_distance))
print(best_distance + ' km')
draw()
if __name__ == "__main__":
solve()
8 结果展示
这里只展示了使用贪心算法和随机算法初始化后的计算结果对比,如果希望对比代码修改前后的效果差异,请自行移步‘python用禁忌搜索算法实现TSP旅行商问题_小白-CSDN博客’获取源码。
8.1 随机初始化
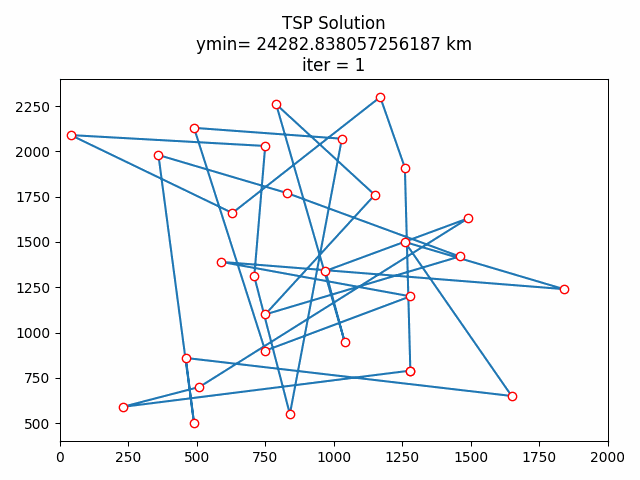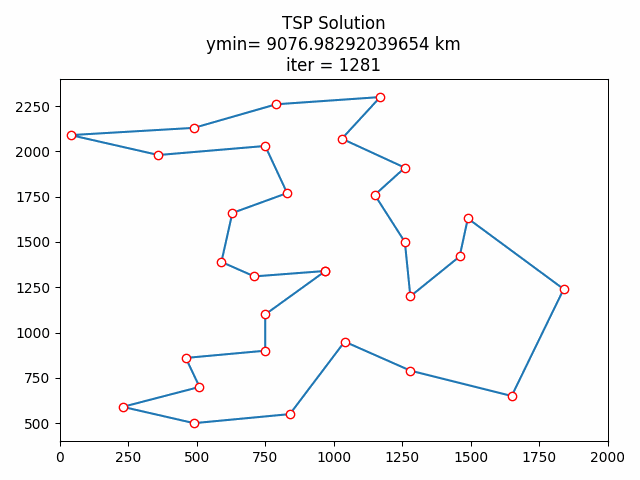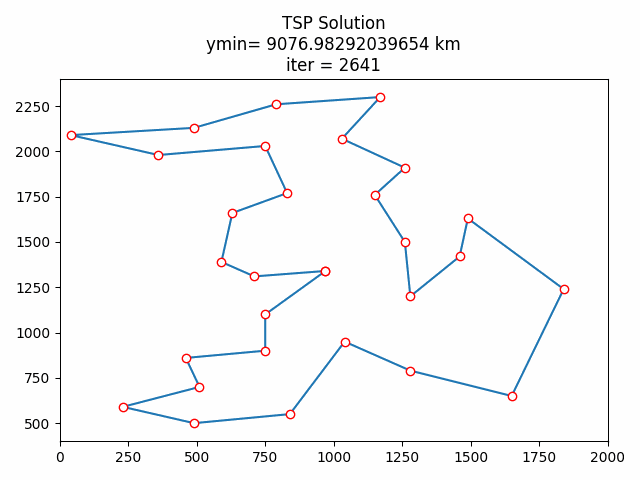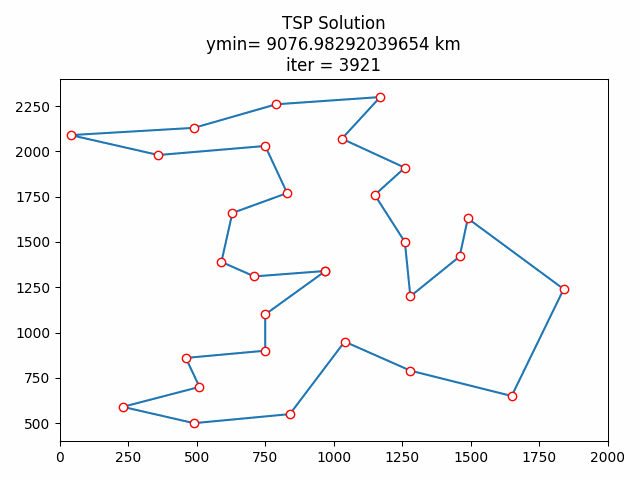
8.2 贪心算法初始化
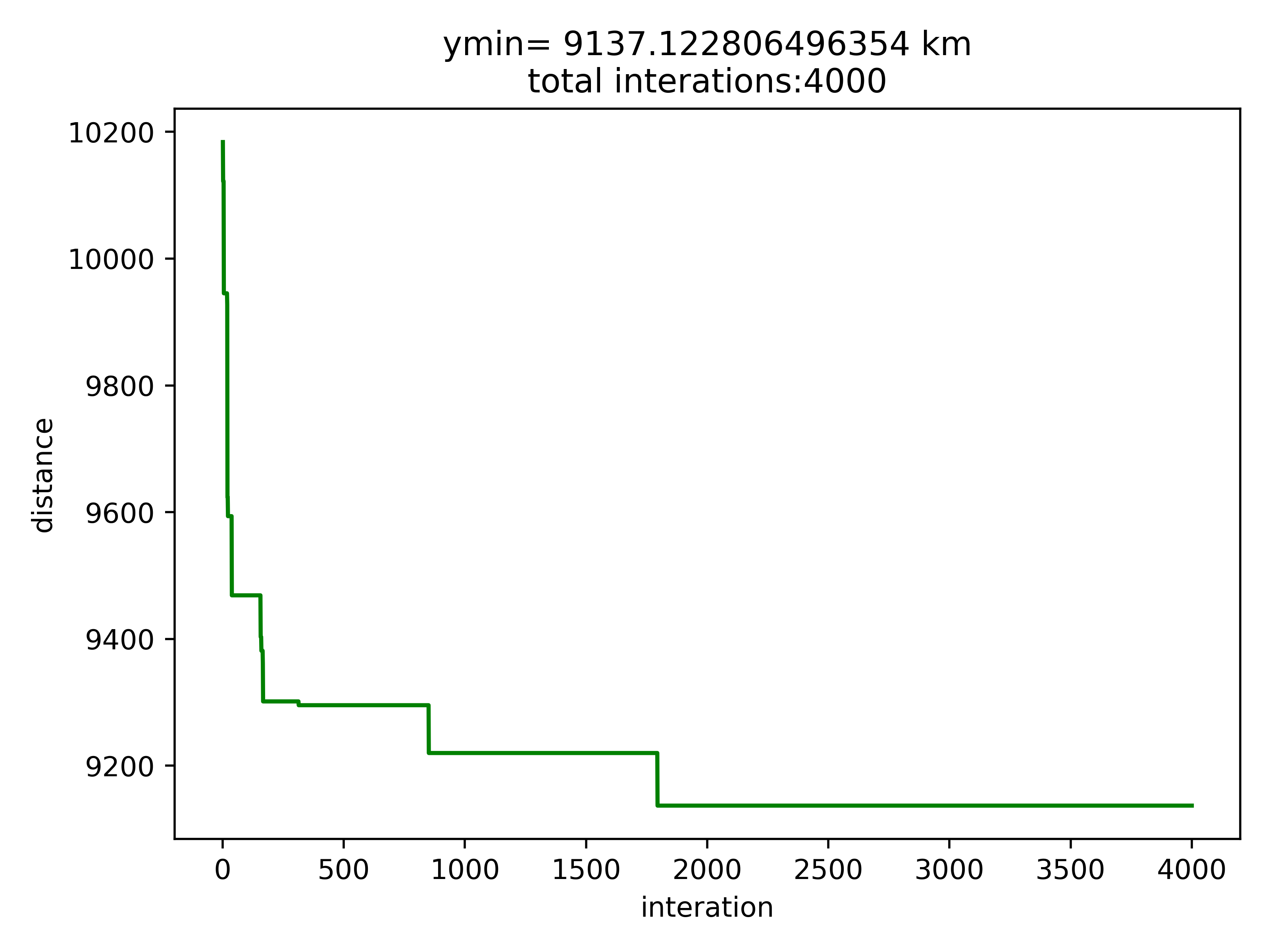
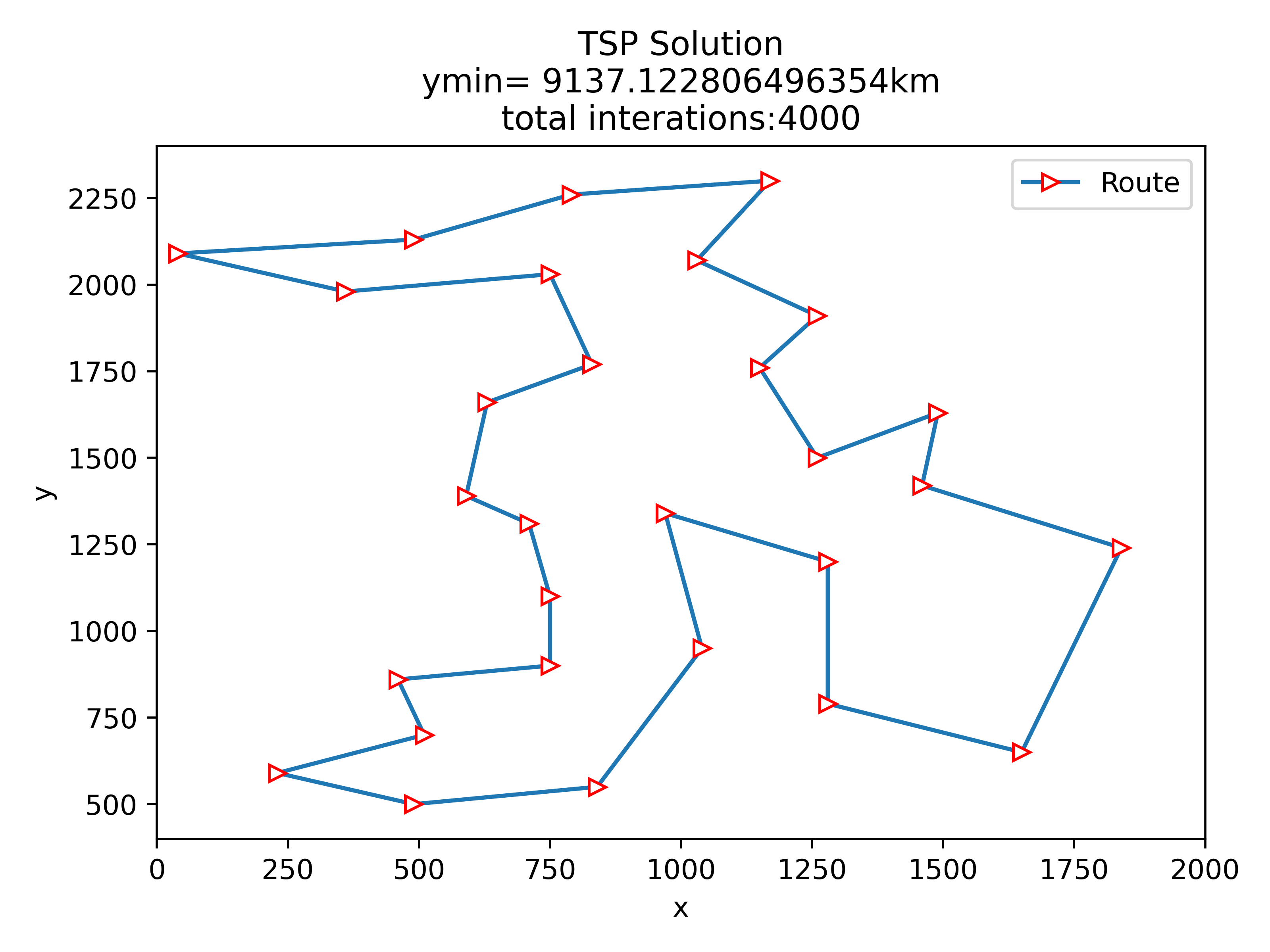
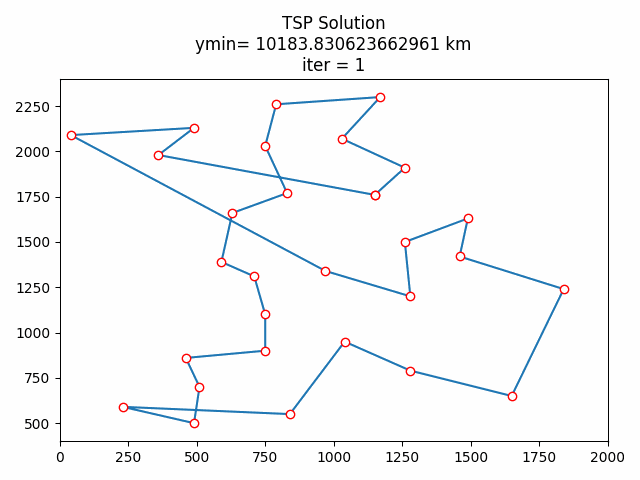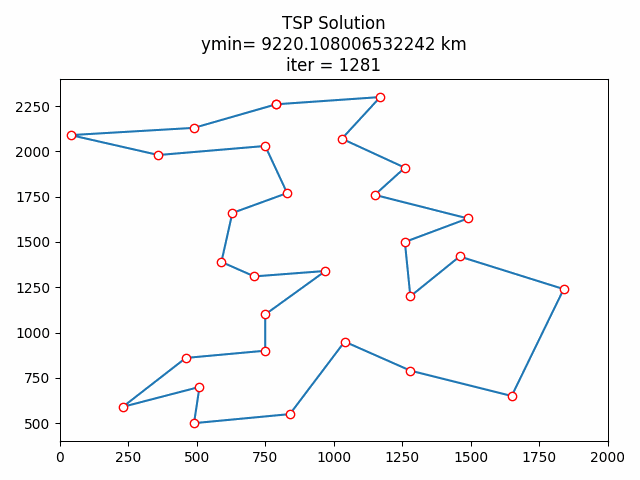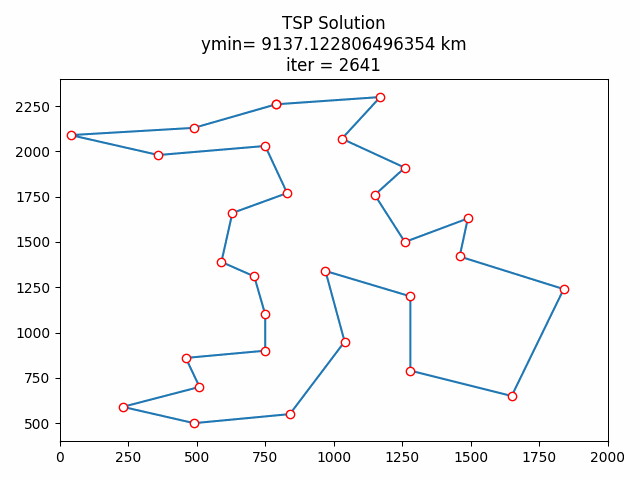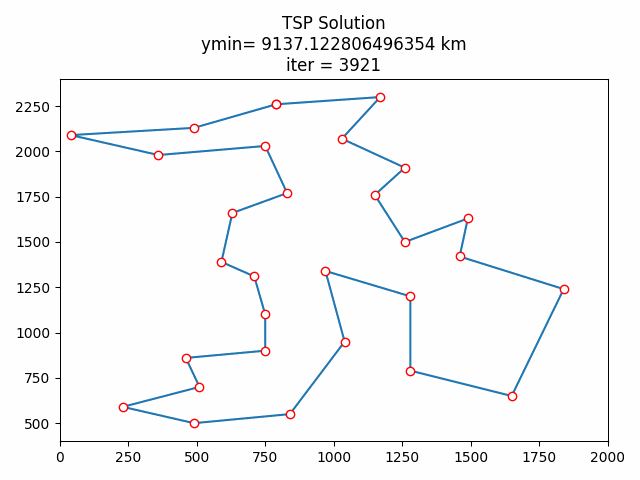
8.3 结果分析
按道理来说贪心算法初始化后的结果应该优于随机初始化的,算完我懵逼了,贪心了个寂寞。
最后
以上就是欢呼小甜瓜最近收集整理的关于禁忌搜索算法学习笔记的全部内容,更多相关禁忌搜索算法学习笔记内容请搜索靠谱客的其他文章。








发表评论 取消回复