一个AI小白如何理解近似匹配检索

在AI领域的相似性匹配中通常会接触很多新名词：ANN、KNN、HNSW、SQ8、Faiss、L2、L1、inner product...你可能会查了很多官方解释，但是：

--> 网上每个名词都告诉了是什么，我知道了他是什么，对，没错，我还是不知道它是什么

--> 根据用户手册，我Step by step成功完成了所有的实验，我依然不知道我在实验什么

--> 有业务场景讲解，与向量搜索/相似度匹配的关系是什么，没错，我也似乎连接不起来

今年有幸接触到“向量搜索”领域，从传统数据库/大数据到这个领域，我也是一个完全的小白，经历了一段时间自认有一点点小入门，觉得还是挺有意思，把一些没太吃透的理解用一些“大白话”分享一下，大家可以当闲聊文章来看。

从一个家庭小故事开始

上周家里小孩有幸参加了杭州某机构组织了小孩子军警技能培训，机构为了满足家长们的朋友圈心态所以给小孩子们拍摄了“非常多帅气的照片”发到某图库中心，图库中心包含了所有小孩的照片，那么如何找到自己小孩的照片就是一个问题，我老婆似乎发现了一个新技能忍不住跟我show一下：你看，我们上传一张咱们孩子的人脸，就可以从所有孩子中找到我们家孩子的帅气照了

-->  没错，这就是传说中的“相似性搜索”/“近似搜索”，在技术层面也可以叫“向量搜索”

--> 为什么是“相似性搜索”：因为每个人会有表情变化、服装变化、侧面角度变化、距离变化、光线变化等等，无法用传统意义上id=id的方式来匹配一个是否等于来确定唯一性（这里细节上我与家人探讨了为什么带着墨镜的小孩帅气照没识别出来，我理解人脸特征提取中比较重要信息会在眼角上）

--> 为什么技术上又是“向量搜索”：一张照片需要有一个体征提取过程，假设人脸上有100个特征，那么可以提取出来100个数据记录下来记录一个人脸（可先粗略理解为每个特征数据点一般用一个float来表达），我们把它叫100维向量数据，所以匹配的时候就叫向量匹配。更形象点理解：假设人脸只有2个特征数据，取出来的2个数据（2个float数据）相当于在x、y轴二维平面的上的1个point位置，相应的如果是3维就是在3维空间的一个point位置。

--> 如何理解特征提取过程（embedding）：特征提取方式与模型有关，不同的模型对同一张图片提取出来的特征维数和值都不一样，对于我们小白来讲，咱们可以业余一点去理解就是一些距离、角度、位置、比例的信息组合（进一步还需要一些神经网络知识对变化的综合理解学习，否则无法对表情的变化无法去识别匹配，我们暂时先不关注太多否则很难理解），总之无论是一张图片、一段音频、一段文本、一个化学分子式可以embedding提取出多个特征点。接下来的内容，我们假设已经存在这些特征数据了，分析下这些数据做近似匹配。

从最简单的“1维”开始理解“相似性匹配”

假设在传统数据库中，有1个表是学生成绩表，常见的业务是取出班级前三、前十、倒数前三、比谁成绩更好的人、平均分、最高分、最低分、成绩分布图、按照学生姓名精确或Like匹配取出学生成绩等。

有一个新的需求：取出与“小明”同学数学成绩最接近的20个同学的成绩。传统解法一定是先取出小明同学的成绩，(每个同学成绩 - 小明同学的成绩)，然后对差值的绝对值做ORDER BY ASC以得到结果：“TOP 20个最接近小明同学数学成绩的同学名单”，这就是一种最初级的相似度匹配。

学习过数据库的同学肯定会说，你这是全表扫描（暴搜），可以通过索引方式来优化，所以我们稍微补充一下在传统数据库B+ Tree Index如何处理这个问题：

1. 在“成绩列”上创建索引

2. 查询大于“小明成绩”的数据，并按照成绩排序的LIMIT 20，由于B+树叶子节点链表有序，所以问题比较好得到解决。

3. 同上，取出小于“小明成绩”的LIMIT 20

4. 在40个成绩差值中按照绝对值排序（这样数据量就比较小了）

不过大家应该看得出，即使B+树上玩一些小技巧也可以解决相关的问题，但是方法会显得十分笨拙不堪，且只能CASE BY CASE去解决具体问题。

为了更好地理解问题，我们举一个更加形象的例子，所有同学的成绩：在0-100的直线上分布，小明同学的成绩在直线的一个位置，假设有一个方法，可以从小明成绩的位置“向两端走”，“距离最近”的点就是最接近小明成绩的人。

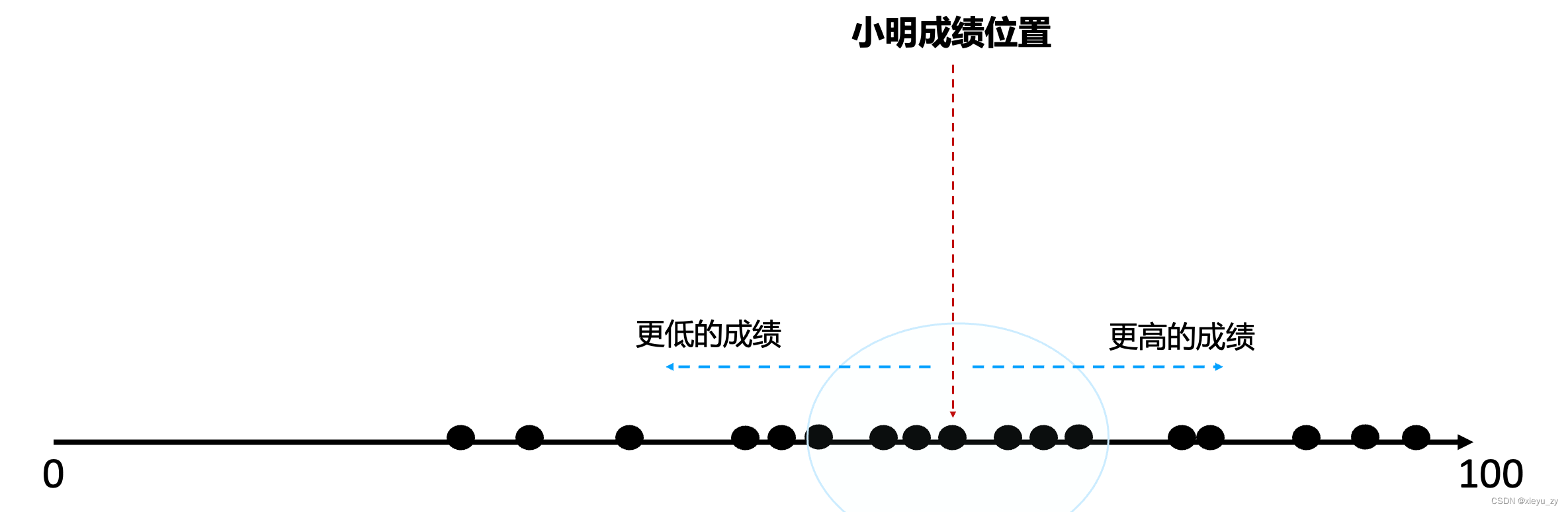
在真正工程落地的时候，1维的场景确实可以用B+树的方式来解决（充分利用B+树叶子节点的有序性来完成图上的工作），如果有更高维度就不行了，为了理解更高维更加容易，我们继续尝试在1维的场景下是否有别的方式来处理该问题。

从上图可以看出数据有“成堆”出现的现象，假设有一种办法可以将他们提前将顺序挨着的多个点组成小组，每个小组有个小组长（或者叫中心点），小明的成绩首先和每个小组长算距离，如果距离太长这个小组就直接淘汰，如果距离近就在小组内与小明判别成绩差，如下图所示：

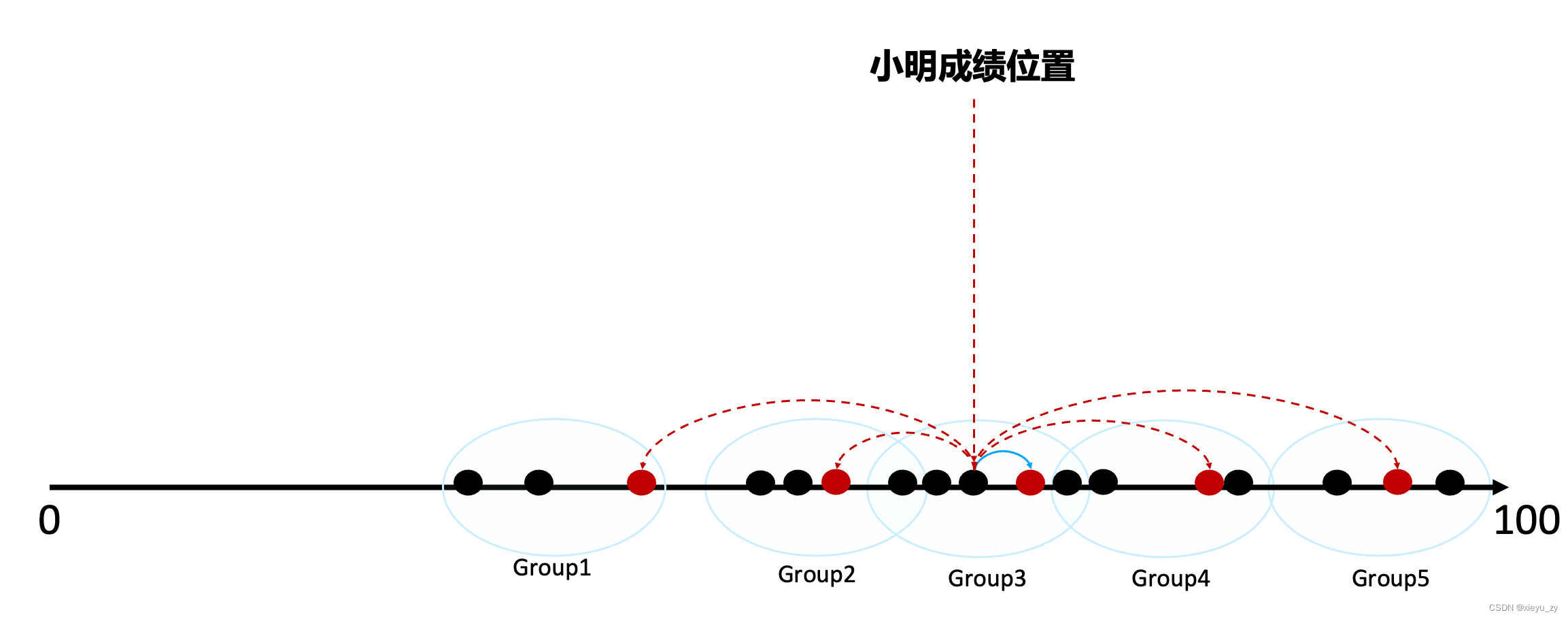
大量的数据可以分布为有限数量的中心点，经过首轮筛选就可以排除掉大量的距离排序“太远”的中心点的Group数据。

每一个数据点也可能被多个GROUP的中心点划分到自己的分组中（在1维中最多到2个Group中），在高纬GROUP交叉会更多。

分组的构建过程大概是：选中心点，计算与中心点的距离、不断调整中心点。至于其中细节技巧，这里由于本人知识所限无法进一步展开给大家讲透。

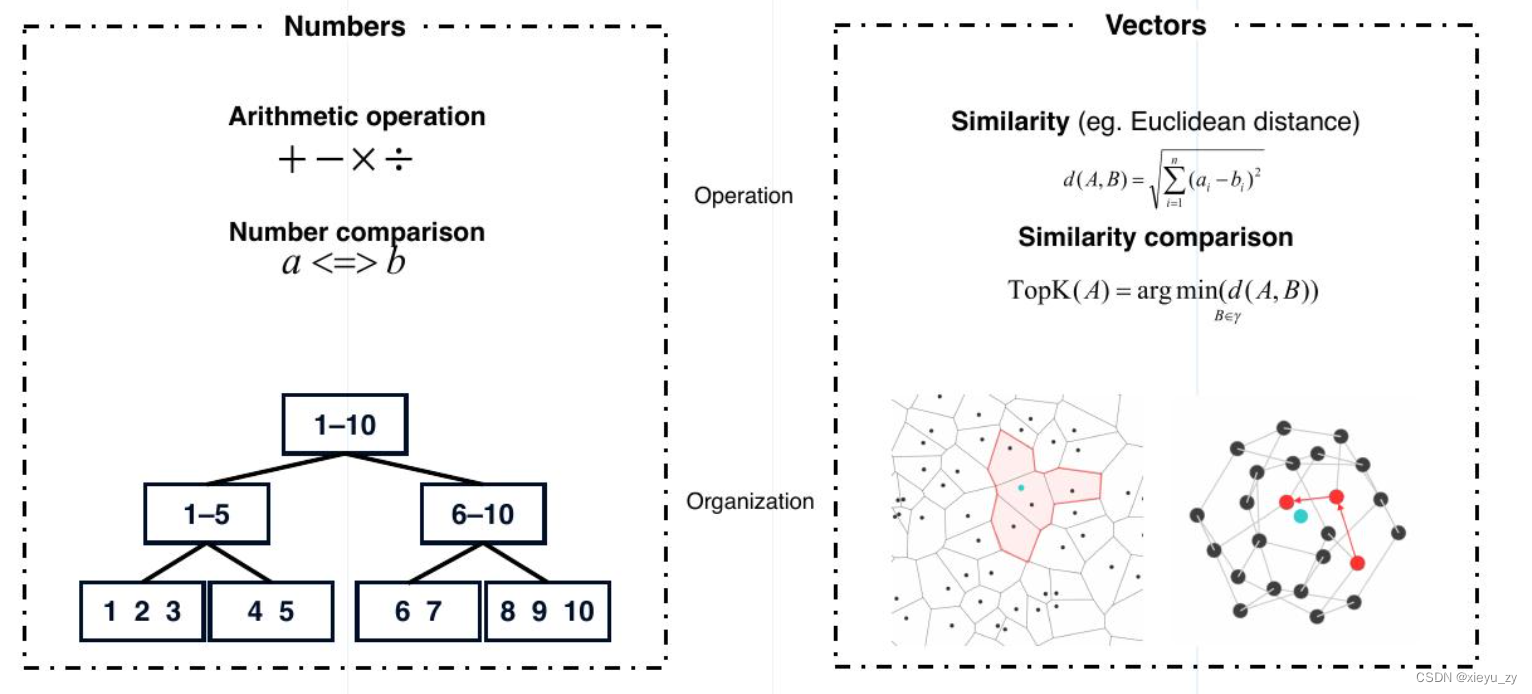
 所以，可以简单的认为近似匹配有点类似：计算空间中点与点之间的距离，真实意义上还有别的方式，我们可以先这样子简单理解。传统意义上的数据比对主要是：等于、大于、小于、不等于、IN、Like等行为，从数学公式上区别如下图所示（转载截图）：

维度提升：2维、更高维

--> 无极生太极、太极生两仪、两仪生四象、四象生八卦、八卦生万物，2进制就是这样子的，^_^

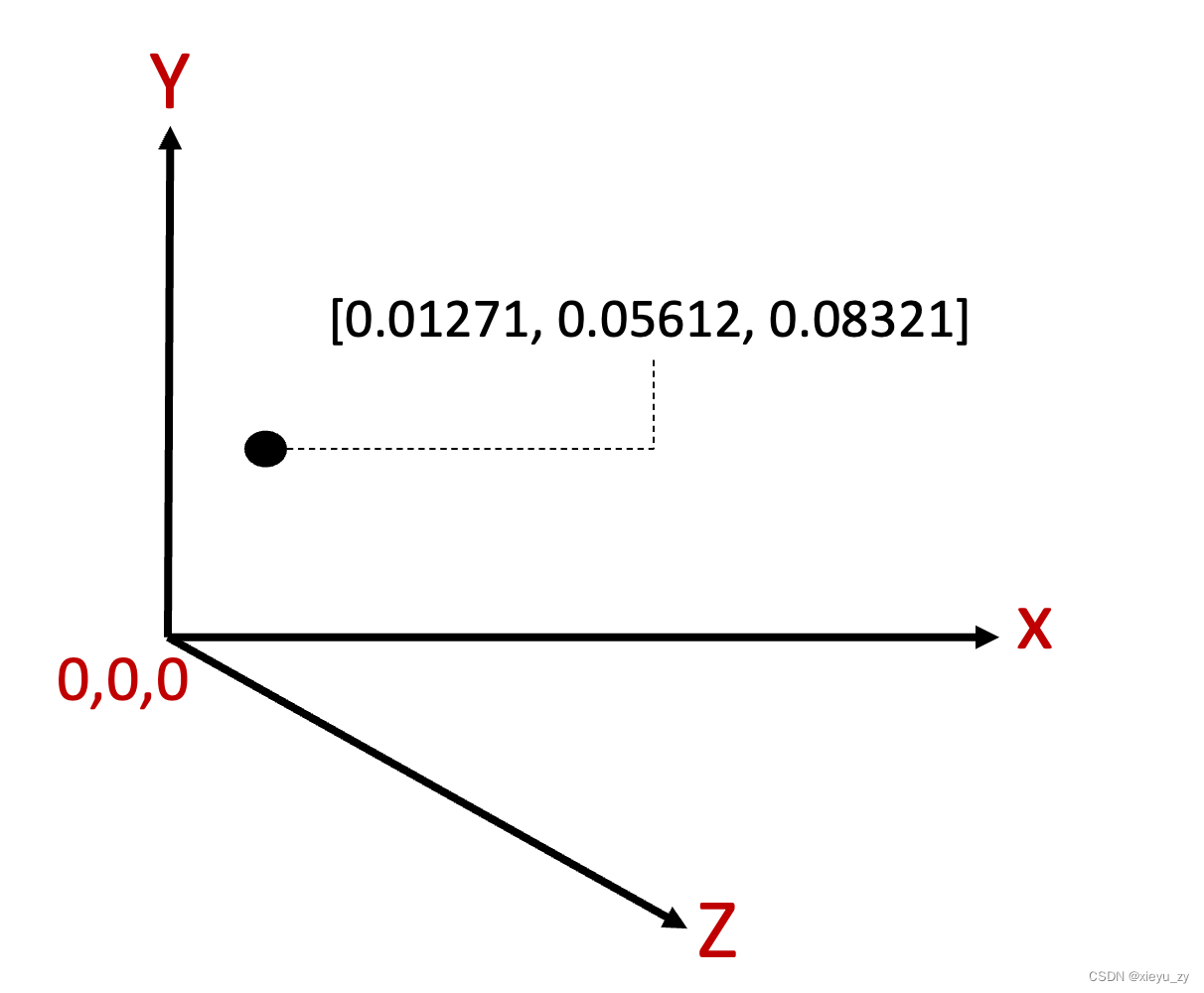
2维数据包含2个数据值，如：[0.01271, 0.05612] ，如果是3维：[0.01271, 0.05612, 0.08321] ，以此类推如果是128维，就是128个数据值。这样一组表达一个高纬空间位置的数据，我们统一可以把它叫做：向量（Vector），所以这些点之间的匹配也叫“向量匹配”，而在向量世界里面，原本数据库的1维数据把它叫做：标量。

如下图，任何一个2维数据始终能在“平面上”能找到一个合适的Point“位置”，如下图所示：

相应的，任何一个3维数据始终能在“三维空间上”能找到一个合适的Point“位置”，如下图所示（在下已尽力，不过很不幸此图依然很不形象，请脑补，^_^）：

至于4维及以上维度的数据，由于我们生活在3维空间，无法完整去理解和表述4维空间存在形态，所以我们只能用公式递推性继续向下探索一些事情。

--> 现实当中的维数一般是2的次方维：64、128、768、1024...

关于“距离”，在二维平面上计算2个点距离，中学数学有一个公式：“欧氏距离”，当然欧氏距离同样可以用于计算三维、四维空间点与点之间的距离，在AI领域简单叫：L2距离，当然除此之外，还有：L1（Hanming距离）、IP（内积）、Jaccard等算法，可参考文档：Introduction - Milvus vector database documentation

通过大量科学实验和工程实践的经验总结，不同的数学公式在不同的业务场景下更适合解决相应的问题，例如L2就比较适合于解决视觉相关的图片、视频等数据。我们先不要想太多，我们就围绕欧式距离来讲，它的计算公式大致如下：

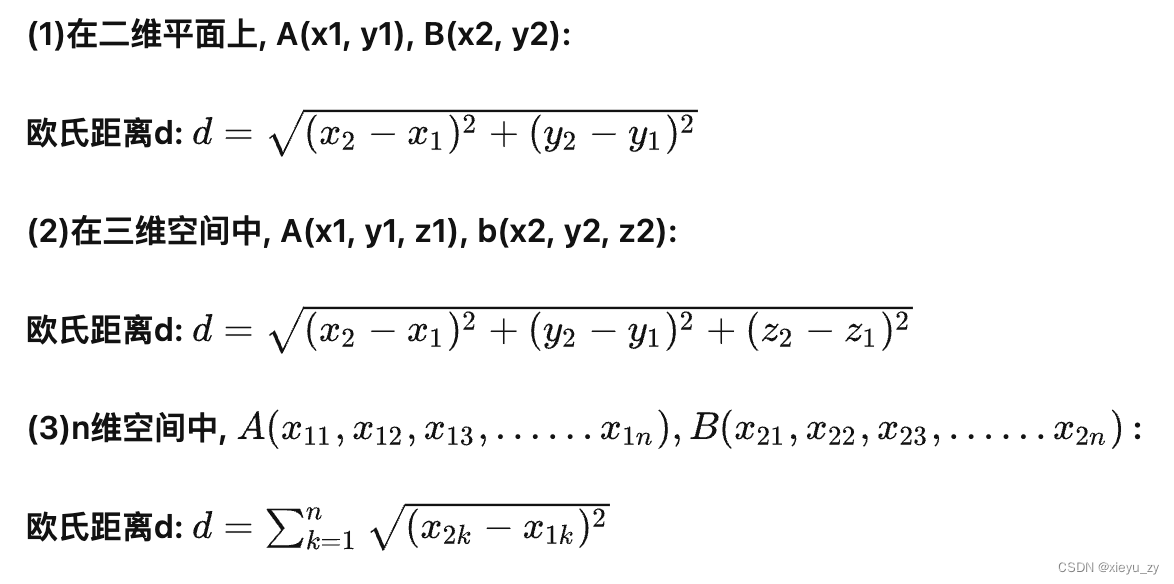
1维：就是平方再开放，相当于2个点的距离取绝对值

每增加1维：根据公式距离一定会在不断变大，因为在叠加下一个维度的距离平方值

以2维为例如下图所示：

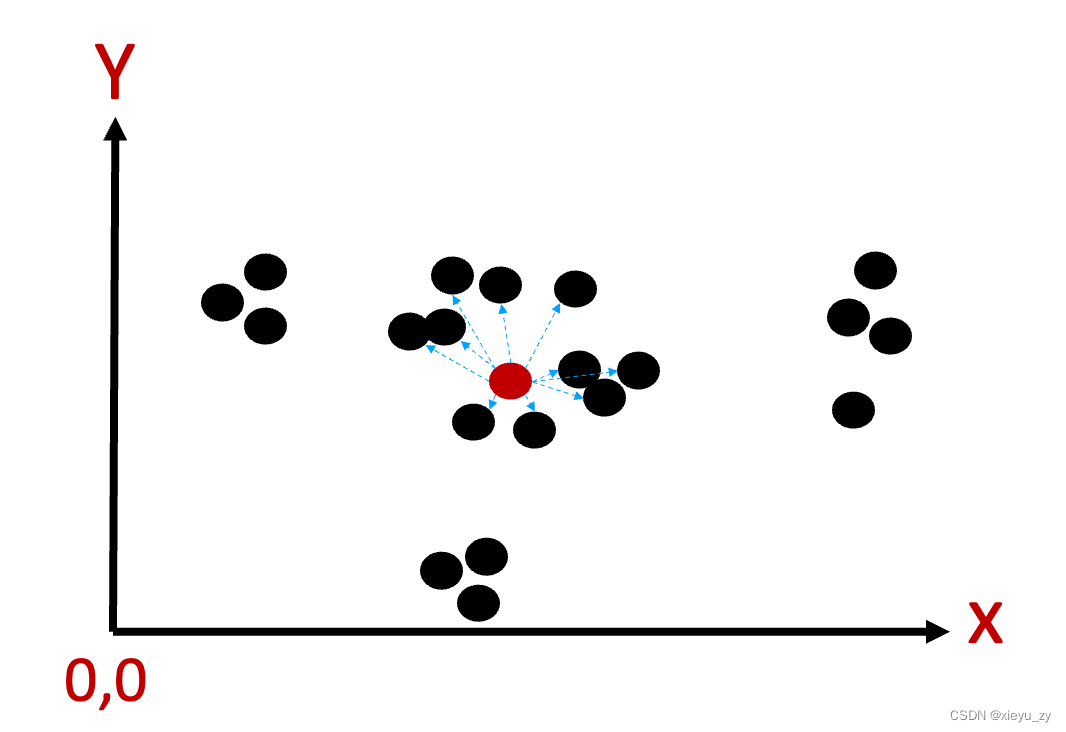
图中红色点代表要找的起始位置，与1维不同的是，1维可以沿着左边、右边两个方向线性去寻找就近的数据，很容易通过B+树叶子节点链表来解决，但2维数据点在其周围360度任何0.00001度旋转方向上都有可能会有接近的点，程序上无法去穷举这种旋转的角度，同时也能看得出来增加1个维其复杂度叠加并不是简单的加法。

因此要寻找接近的点，通过欧式距离提供一种数学公式用于计算点与点之间的距离，不过我们是否将所有的点与检索的点一一匹配呢，在传统的数据库中就是表扫描复杂度为：rows，在向量匹配的过程中如果抛开硬软件优化，按照上述公式得到的计算复杂性应该就是：rows * dim

举个极端点的例子，假设10亿数据普通数据库全表扫描复杂度是10亿，如果是1024d的向量匹配，复杂度应该是1024 * 2 * 10亿 = 20000亿，所以如果不在技术上寻求一些解法，传统的手法只能在少部分场景通过堆硬件来解决，应为你没有办法在同等数据量上去增加2000倍的硬件开销。

要寻找到相近的点就是一种“工程算法”，这里面就需要构建索引，而对照前文在1维空间中的分组，我们如果在2维也用类似的方式来做，会是什么样的呢？

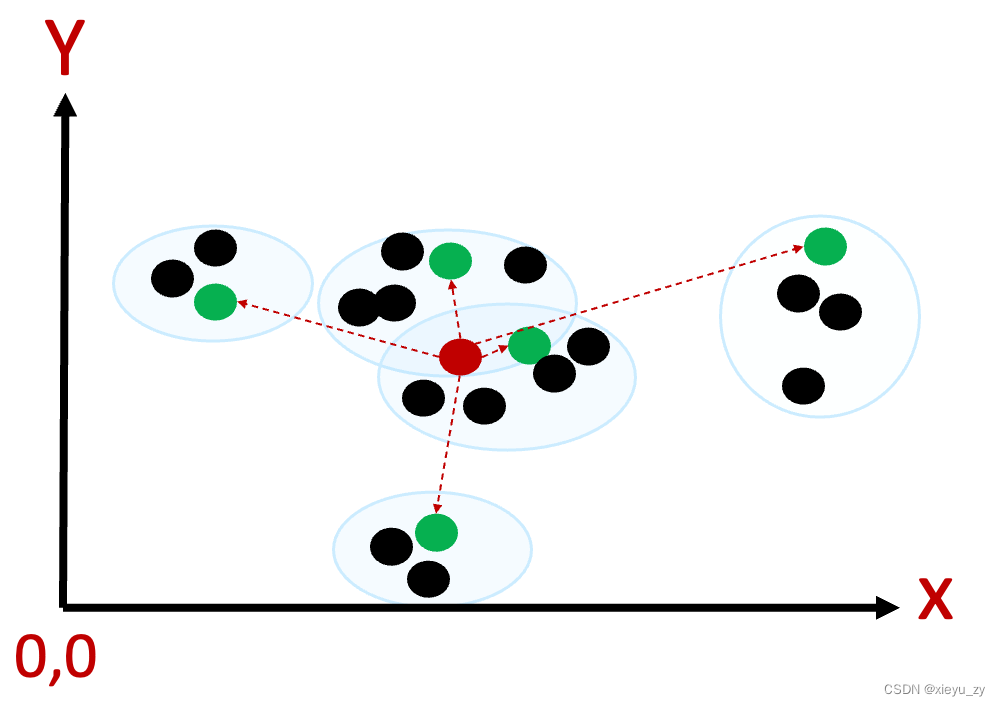
这种方式向量匹配索引中也叫：“Quantization-based”，在Quantization-based indexes实际运行中，中心点是通过所有点的算数平均值得到一个“逻辑点”，这样可以确保一个分组内所有点与这个逻辑点的距离距离较为接近。

此时假设有1000个中心点，每个中心点有1000个点（共计100万个向量），此时输入需要计算的点：q。

• 将q与1000个中心点计算距离并按照距离排序，这些距离可以先做1次排序，根据空间分组的规则，可以理解如果q与某分组中心点距离比较远，那么与其分组内元素的距离大概率也会比较远。
• 根据检索参数，从中心点中取出nprobe个元素，例如取出最近的10个中心点，然后再从这个10个中心点的GROUP中每个元素与q计算距离，并逐步进入红黑树，确保红黑树上只有业务需要的TOP K个元素，循环完成后即得到最终结果。

这种方式向量匹配次数为：1000 + 10 * 1000 = 11000次向量匹配，暴搜自然是100万次，那么这里向量匹配的次数理论上就降低了100倍，同时可以得到一个比较高召回率的结果。

关于“Quantization-based indexes”，实际的索引名包含：IVF_FLAT、IVF_SQ8、IV_PQ，而在真实的向量检索中“Quantization-based indexes”使用效果通常还不是最为理想的，“Graph-based index”（HNSW）的使用更为理想和广泛，除此之外还有：“Hash-based indexes”、“Tree-based indexes”，以及他们之间的组合。

关于几类索引更多理论理解可参考文档：Accelerating Similarity Search on Really Big Data with Vector Indexing (Part II) - Zilliz Vector database learn

关于向量数据库索引的具体使用和参数请参考：

Vector Index - Milvus vector database documentation

是否可逐维比较距离用以降低计算量？

计算A、B与目标C比较谁更近，如果第1维A更近，是不是第2维就不用比较了？如果是这样就可以大量节约计算量。

然而并不是，举个极端的例子，假设C正好是[0, 0], A和B分别是：[3, 1], [1, 4]，显然第1维B距离C会更近，但是整体距离，B距离C会更远。所以，在高纬空间比较，并不能用传统上通过逐维比较后降低运算规模来达到优化的目的。

尝试补齐算法与工程的GAP

本文虽然没有深入去讲解AI知识，不过大家应该可以从上文中可以看出，AI领域的计算玩法相对传统数据匹配的玩法更加抽象，需要更多的理论知识储备，不能直观去理解和推导他的逻辑关系，但实际运算过程中，又需要计算机理论的真实落地，才能让AI真正低门槛低成本地普惠大众，这两者之间有着不小的Gap通常让AI算法领域和计算领域的人在相互听天书一般，彼此之间的能力无法发挥到极致，这也许就是我们去努力完成的工作和机会，所以我们来看看行业中现在的玩法和未来可能更加理想的玩法。

烟囱模式，一家公司基于业务场景CASE BY CASE做，基于特定业务场景做特定的优化，例如：某公司知道向量的维度、数据量后，将所有的向量全部装入多台机器的多个GPU当中成为底库，然后充分利用GPU的并行计算能力计算多维数据，加上机器也可以并行，就是疯狂用硬件成本来对抗业务要求。如果你需要更大的QPS，可以提供更多的副本来完成。当然这肯定是一种玩法，还有更多基于具体场景的千百怪的玩法，从模型、embedding、存储、装载、检索计算都可以case by case做，即使在同领域内的可复用性也不高只能试。

--> 长久看，未来的世界不应该这样子的

半烟囱，使用一些三方成熟会半成熟的套件，用以组合用户的需求，已有套件如果能完成的直接使用，不能完成的尽可能适配，不能适配的看能不能改，不能改的就自己做，业务层依然是烟囱式CASE BY CASE做，只是会少一些。

分层模式，按照我自己的理解（还未有三方参考依据），层次大致会是这样子划分：

1. 基础研究性的工作，我理解是高校、科学家、大厂的科学研究组织去探索新的数学算法的可能性，我理解科学家也都不是神，几乎不是像爱因斯坦那样通过数学公式推导世界规律，或则说不是推演出“相似性匹配”一种新的数学公式，目前使用的公式大多也是以前数学教材中的公式，更多还是“尝试和不断实验”的方式得到的结论，另外，具体一些场景结论也有来自于工程界的实践经验反馈。

2. 基础设施产品，如果没有这一层，前文提到的诸多问题以及还有更多未提到的工程问题需要在每个业务自己去重复花费大量精力去解决，数学公式在计算机里面要么得不到充分的发挥、要么可能需要数倍的硬件成本，除非有一群数学领域和计算机领域两方面都很强的人，但大多也只是在某个公司基于场景解决问题，无法将其能力复制。如果有一群人专注在这个方面解耦技术和应用，将数学算法、工程算法的有效结合，将其做成像类似数据库、NoSQL、大数据一样的引擎，那么上层的AI应用型产品就变得更为简单直接。

当然要做到这一点很不容易，没错，写了这么久，实在是憋不住的广告终于要发出来了^_^，国产自研向量引擎Milvus是一个咱们的骄傲，在AI基础软件设施这个赛道上无论是开源热度、开源界AI赛代的影响力、用户的涉及面都是王者位置，具体请参考官网和开源代码地址：Vector database - Milvus   The Milvus Project · GitHub

3. 原子AI产品，如果有了基础设施这一层，这些原子服务的开发变得非常简单，可以少关注很多问题，更加关注于数学算法、数据本身的选择，构建一个原子应用的时间和维护成本就变得很低了，同时可以有单独的团队来维护和优化，在云上大部分可以交给云服务去完成（云服务的正式release尽情期待）。

4. 原子积木化的AI服务有了，距离真正的业务还差一步之遥了，帮助业务成功也还需要理解业务需要解决核心问题，积木化的服务除了稳定和性能外还需要有很强的灵活性，方便积木构建过程中去调整细节，同时需要有比较标准化的接口和规格参数，这样在构建真实的业务应用的时候就会变得“可复制性”很高，否则会非常难用（还不如自己搞）。

这样以来，即使是具体的业务的解法可复制性并不高（具体的业务种类可能会上百种），但如果每一种的解法的定制成本足够低（当然前提是：每一层下面一层的积木需要足够好用），再结合现代的流程编排工具进一步降低定制成本，这一层大家依然可以在投入产出比上获得更高的收益率。

也许这是一种比较理想的共赢局面，也许还有比较长的路需要去走，AI这个道路很多未知的区域需要我们大家一起去探索，这个文章很多内容是我一个小白的理解，内容可能有错误的地方请大家“照死里拍砖”，我应该会“选择性接受”  ^_^，后续如果有幸获得更多理解后续再补充。

最后

以上就是含糊板凳为你收集整理的一个AI小白如何理解近似匹配检索的全部内容，希望文章能够帮你解决一个AI小白如何理解近似匹配检索所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。