--NeoZng【neozng1@hnu.edu.cn】
-
IOU loss family
在之前训练bbox regression分支的时候,我们只利用了回归得到的角点与GT角点坐标差的模值(若是利用中心点和长宽也类似,用MAE、RMSE、Smooth L1等LF),仔细思考一下就会发现这存在一些问题:实际评价检测效果的时候使用的指标是IOU,但显然我们loss的设计目标和评价指标不等价,多个检测框可能有相同的Loss但IOU的差异可以特别大,为了解决这个问题IOU loss就自然而然诞生了。
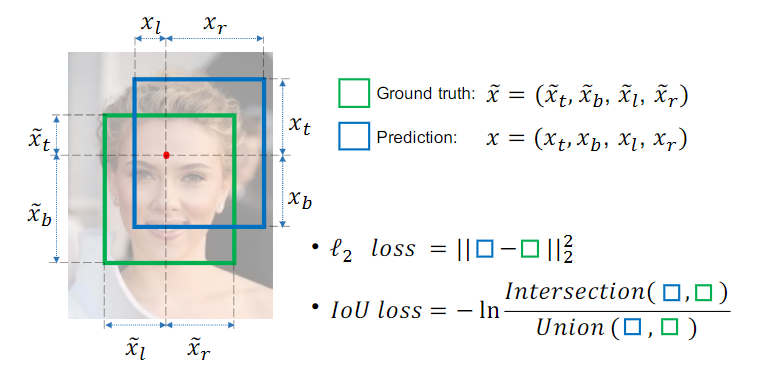
截取自论文原文,这里对比了L2 loss 和IoU loss
IOU loss用IOU来评价bbox回归的好坏,这样就统一了评价指标和训练指标,同时还让bbox regression拥有了尺度不变性(原来的距离loss对于不同大小的样本不具有这个特性!)。
欸那有人肯定又会说了,即使IOU相同,回归效果的好坏也会有差啊,不信你看这个:
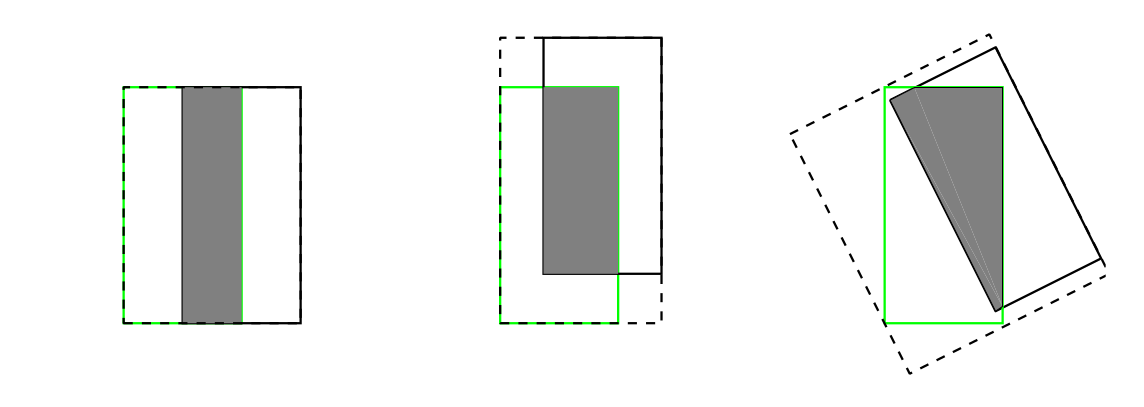
以上三种情况虽然predict和GT的IOU相同,但是他们的回归效果肯定不同
而且在刚开始训练的时候,万一预测的框离GT很远,根本没有产生交集那IOU不就一直是零吗?那么有没有什么办法可以改进IOU loss让他可以区分相同IOU情况下回归效果的好坏并解决预测bbox和GT交集为零时如何训练的问题?GIOU给出了答案。首先找到一个能够包住GT和预测框的最外界矩形C。然后计算C的面积减去(GT ∪ bbox) 的面积的差与C的面积的比值,再用GT和bbox的IoU值减去这个比值得到GIoU。
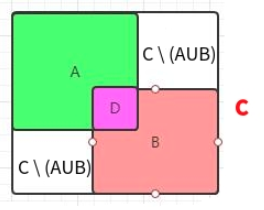
符号表示集合运算中的减法,定义为C(A∪B)定义为C中有而AB并集中没有的部分
略加思考你就会发现,GIOU loss会使得IOU尽量大,而C(A∪B)尽量的小,那么在bbox和GT尽量对齐的时候,GIOU值会更大,这就在很大程度上解决了前一张图片中出现的无法区分的问题。下面这张图展示了不同情况下L2 损失、IOU loss和GIOU loss的大小:
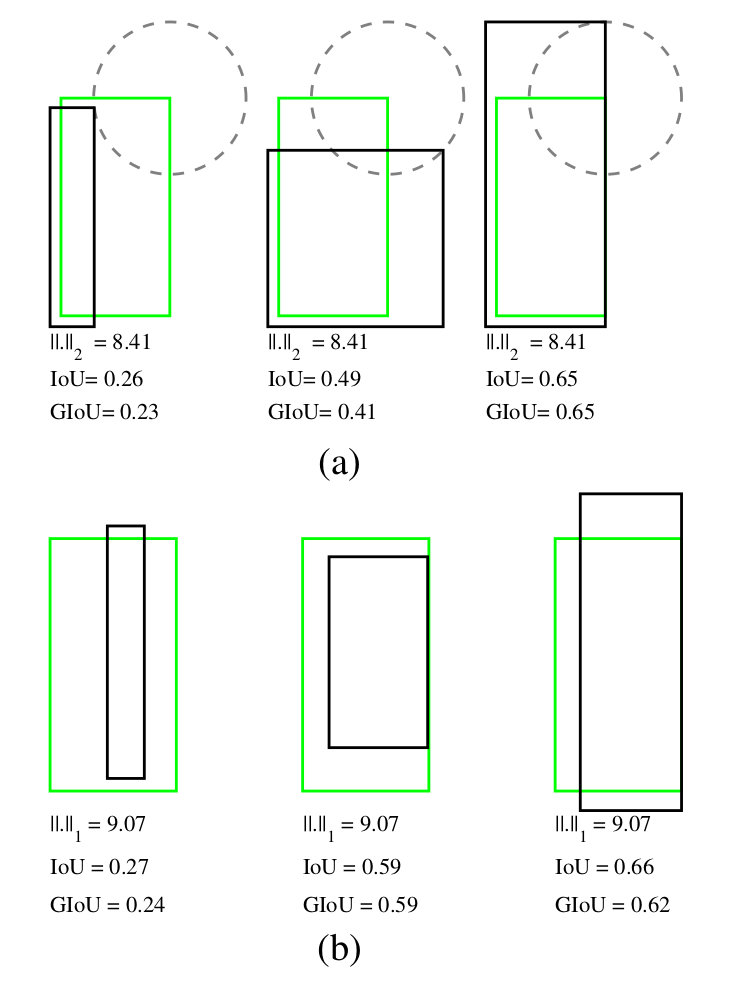
对比下来,GIOU拥有最好的评价效果
既然IOU loss已经在这里开了个大坑,大伙就都在想能不能再这些个loss的基础上再挑挑刺,进一步细化评价标准?还真有,CIOU这不就来了,而且这帮作者还直接一下提了俩,除了CIOU还搞了个DIOU,还给不给人活路了,分我也发俩篇撒。
论文作者着重考虑了bbox回顾的三个要素:重叠区域,中心点距离和长宽比。从这里入手首先提出DIOU:在IOU loss的基础上添加了一个bbox和GT中心距离的惩罚项,以此为目标进行训练将会逐渐把两个框拉在一起。但是能保证他们对齐程度一定提高吗?CIOU紧随其后,又在DIOU的基础上额外增加了一个bbox的长宽比的约束,让loss能够更快地收敛。对比GIOU,GIOU的损失函数似乎也在做类似的事情,不过它把这两个工作给糅合在了一起而没有在两个方向上分别发力,颇有些”不偏科也没强项“的感觉。CIOU则把中心点距离和长宽比分开考虑,认为他们的作用是正交的,并对两个因素进行专门的优化,从而获得了更好的效果和更快的训练速度。
这就像线性代数中的特征值分解/正交分解,把原本糅合在一起的特征或属性在不同的维度/基底上分开考虑,最后再叠加到一起。这也是信号处理的惯用”伎俩“了(fourier、laplace等等)。
同时作者指出在NMS的时候使用DIOU可以获得比简单的IOU更好效果,论文还对GIOU的drawbacks进行了鞭尸分析,通过实验指出了IOU family前任们的局限性,感兴趣可以戳 Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (arxiv.org)。
-
GFL
GFL的全称是generalized focal loss,看名字就知道,extend、generalize、complete啊这类的基本都是在原有论文的基础上得到启发进一步得到的结果(这说明多看论文就能发paper)。
观察IOU family的实现方法,我们发现IOU分支是和分类分支独立的两个分支,特别是使用解耦head的结构,训练的时候各玩各。而且前人的ablavation也已经证明定位框的准确性和分类准确度并没有很大的关联,因此在训练和预测的时候,两者输出的结果存在一个gap,一个分类置信度很低的bbox却很有可能在IOU分支中获得很高的分数,最后在计算得分的时候将两者相乘就会得到异常的结果。那GFL的解决方法就是,在训练的时候联合两者的表示(representation,定位质量表示框准不准,也就是前述iou family解决的问题,分类表示如one-hot或者softmax的输出,还有用分布来衡量的方法)。

这样,在训练的时候,把原来的one-hot label转换成分类与质量估计联合的连续label(即one-hot label乘上该预测框和GT的iou作为新的训练标记),将这个label作为分类和质量估计的指导,从而消除训练和推理时的gap(似乎显而易见!但是之前却没有人想到)。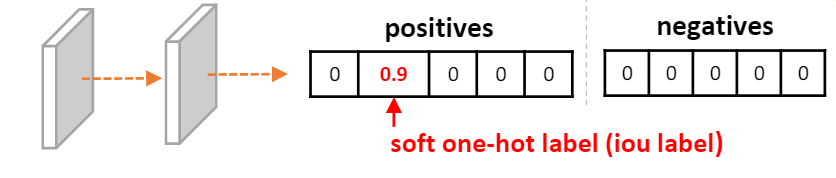
因此对于FL的第一步修改,得到了如下的表达式:
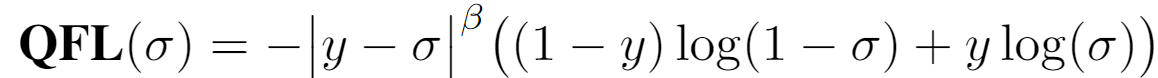
σ就是添加了框质量预测的分类估计值,y是乘上了iou的标签
第二个问题是框的表示,在以往的传统框回归中,实际上是让网络学习一个狄拉克分布(冲激函数),即对一个以图像长宽为横纵坐标,框位置为输出的一个函数;也有一些方法尝试为框的回归简历一个高斯分布,即训练目标是得到以训练label为中心的一个尽量集中的高斯分布。GFL的想法则是不去人为指定或设计一个框的分布,而是让网络自己学习这个任意分布(颇有一种粒子滤波器的感觉)。
想要得到预测输出,根据概率分布函数的定义,就对整个区间进行积分:
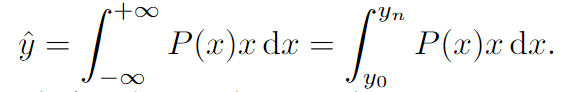
因为图像是一个二维离散平面每一个坐标轴是离散的,所以我们把区间划分成n个小区间,将其离散化:
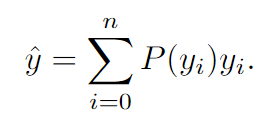
若要回归的更精确,就将区间间隔变得更小,反之增大,极限情况就是一个像素一个区间. 根据概率分布函数的特点,我们希望在积分区间内积分得到1,聪明的你肯定已经想到我们可以用softmax来输出整个离散分布!不过这里还存在一个问题,一个积分值可以对应无穷种分布函数,这就会大大降低学习的效率,使得框的分布不能很快地收敛(每个label都大概率会导向不同的分布,虽然他们的总体收敛方向相同,但是中间有很多个step都相互抵消了)。从直观上考虑,下图(3)是比(1)和(2)更好的分布,因此作者对损失函数稍加约束,提高离label最近的两个位置的权重使得分布能够更快的收敛,否则增加的权重可能被放在距离label处更远的地方,如下图(1)。
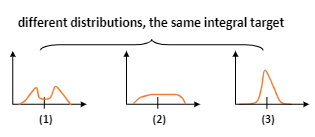
不同中分布积分得到相同值(横轴竖线)
最后得到的DFL(distance focal loss)就是如下的形式: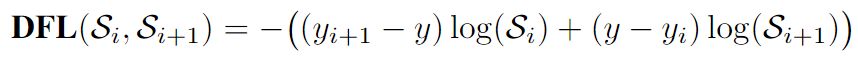
其中yi和yi+1是第i和i+1个位置(这两项看起来和cross entropy也有些相似,其实是在计算预测分布输出和标签的差异),y是标注的Dirac函数(即标注框的位置)Si和Si+1是分布函数在yi和yi+1处的值(也就是前文公式中的P(yi))。那么每次计算两个位置,若长宽都为100像素则需要计算99+99=198次。
不得不惊叹作者的loss function设计之巧妙,最后还将QFL和DFL进行统一,得到了一个GFL的表达式,有兴趣的同学可以自行参阅原文:https://arxiv.org/pdf/2006.04388.pdf 。作者在知乎上也有一篇讲解的文章,戳这里:大白话 Generalized Focal Loss - 知乎 (zhihu.com)
强烈推荐下载原文并且精读,它对于之前的预测框几种表示的洞察十分深刻,且这篇文章的数学方法并不算难而且对FL和IOU loss 提出的针对性的优化思路非常清晰明了,很适合入门后的进阶。随后作者还推出了GFLv2的版本,感兴趣自行搜索阅读。
如果觉得笔者写得还不错,点个赞加个关注吧!
flag:本专栏今天开始一星期两篇
最后
以上就是雪白衬衫最近收集整理的关于(五)比赛中的CV算法(下4)损失函数的改进(2)如果觉得笔者写得还不错,点个赞加个关注吧!的全部内容,更多相关(五)比赛中内容请搜索靠谱客的其他文章。








发表评论 取消回复