之前几篇有关HMM模型的文章（隐马尔可夫模型（一），隐马尔可夫模型（二））主要讨论了这个模型的理论部分，从这篇文章开始，我们从实际的应用场景入手，看看应该如何使用HMM模型以及它的代码实现。

与传统的机器学习模型分为界限明确的监督式学习和非监督式学习不同，HMM可以处理这两种场景的问题（这其实是所谓生成式模型的优点）。而这篇文章将先讨论监督式的场景，下一篇文章（隐马尔可夫模型（四））将讨论非监督式的场景

注：在Github上可以下载本文所使用的数据和模型代码。

一、中文分词：监督式学习

在对中文进行自然语言处理时，分词是其中很重要的一步，也是隐马尔可夫模型很典型的应用场景（监督式学习）。下面就来详细讨论中文分词的详细步骤。

所谓中文分词就是将句子里的一个或多个文字组合在一起构成中文里面的语义单元，也就是日常生活中词的概念。比如“我爱北京天安门”这句话就分为4个语义单元，分布是“我”“爱”“北京”和“天安门”。

为了能到达上面的分词效果，我们首先需要将其转换为模型能处理的分类问题。具体地，假设文字一共有4种状态，分别以字母B、M、E、S表示。

• 字母S表示当前文字单独成一个语义单元。比如上面例子里的“我”和“爱”字。
• 字母B表示当前文字是一个语义单元的开头，且该语义单元包含多个文字。比如上面例子里的“北”和“天”字。
• 字母M表示当前文字在一个语义单元的内部，比如上面例子里的“安”字。
• 字母E表示当前文字在一个语义单元的结尾，比如上面例子里的“京”和“门”字。

经过这样的定义后，任何一个中文句子都对应着一串字母序列，比如“我爱北京天安门”这句话就对应着序列SSBEBME。反过来，如果知道了一个句子所对应的字母序列，那么分词就是一件很简单的事情了，比如从字母序列SSBEBME可以很容易得到分词的结果：S/S/BE/BME。因此，只需搭建模型对每个文字进行分类即可。这样就把中文分词这件看似无从下手的问题转换为了熟悉的多元分类问题¹，如图1所示。

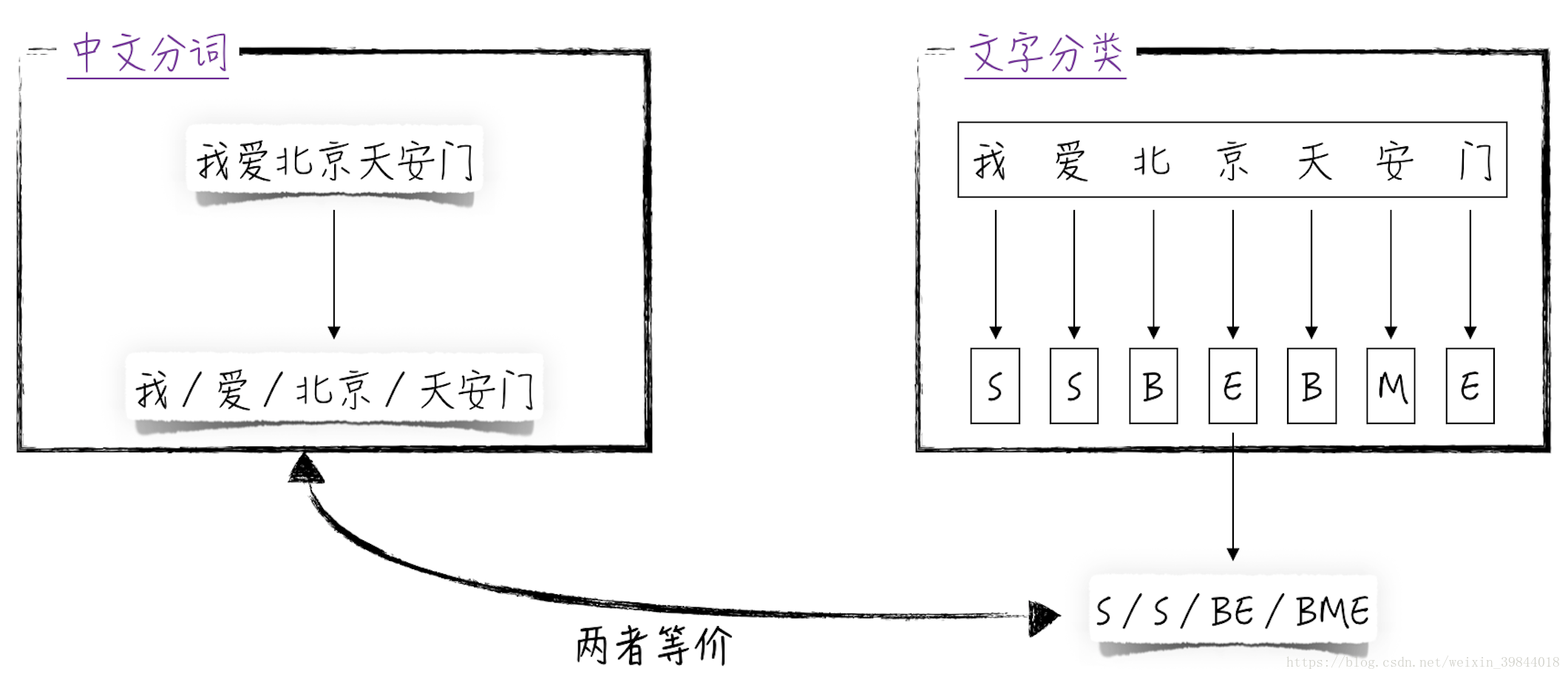图1

显然在这个问题中，文字之间不是相互独立的，比如如果一个字的状态是$B$，那么紧接着它的文字不可能是状态$S$，于是使用隐马尔可夫模型来解决这个分类问题。

具体地，用变量$y_i$表示第$i$个字的状态，根据上面的假设$y_i$可能的取值有4个；用变量$x_i$表示第个字具体是什么文字。根据隐马尔可夫模型（二）中的讨论，现搭建模型如下。

• 先验概率$P(x_i|y_i)$：在已知文字状态的情况下，每个汉字出现的概率。针对这部分概率，使用多项式模型，假设$P(x_i=k|y_i=l)=p_{k,l}$。
• 初始分布$P(y_0)$：表示每句话第一个字的状态分布，这个比较直接，假设$P(y_0=l)=a_l$。
• 转移矩阵$P(y_i|y_{i-1})$：表示4种状态间相互转移的可能性，这部分也比较直接，假设矩阵的元素为$P(y_i=l|y_{i-1}=t)=b_{l,t}$。

在中文分词这个问题中，我们能够观察到被预测量$y_i$（在实际应用里，字的状态来源于人工标注）。因此根据最大似然估计法的原则，容易得到上述参数估计值的解析表达式。

$$\begin{gathered} {\hat{p}}_{k,l}=\frac{C(x=k,y=l)}{C(y=l)} \\ {\hat{a}}_l=\frac{C(y_1=l)}{C(y_1)} \\ {\hat{b}}_{l,t}=\frac{{\sum }_{i}C(y_i=l,y_{i-1}=t)}{{\sum }_{i}C(y_{i-1}=t)}\text{\hspace{1em}(1)} \end{gathered}$$

公式（1）中$C$表示事件在训练数据中出现的次数，比如$C(y=B)$表示在训练文本中，状态$B$出现的次数（不管它的具体位置是什么）。由此可见，这个隐马尔可夫模型的参数估计值与多项式模型非常类似，都是具体事件在训练数据里的占比²，因此在学术上这个模型被称为用于监督式学习的multinomial HMM。

二、中文分词之代码实现

虽然用于中文分词的multinomial HMM模型比较简单，但遗憾的是并没有成熟的开源解决方案，大多数开源算法都是用于非监督式学习的multinomial HMM。不过如果理解了模型的原理，用Python实现这个模型并不困难。限于篇幅，代码的细节在此就不展开了（对工程实现比较感兴趣的读者请参考随书配套的代码yahmm/hmm³），仅讨论在模型的工程实现中比较重要的几点。

1．单元测试

就程序本身而来，模型的实现并不复杂。通常只需要几百或者几千行代码，但与普通的程序相比，模型本身包含了比较复杂的数学逻辑，很难保证编写的代码就是想要的模型逻辑。因此单元测试就显得极其重要了，否则很容易陷入这样的困境—“当模型效果不好时，不知道是因为自己的模型搭得不好，还是因为代码写错了”⁴。而且做单元测试时，不能只简单地测试功能是否实现，更需要用人工计算的模型结果去验证代码的逻辑是否有问题。

对代码做单元测试通常会用到一些自动化的辅助工具，在Python中，nosetests是一个不错的选择。

2．Cython

Python虽然很简单易学，但它最大的问题是运行速度太慢，用Python来做机器学习的模型运算几乎不可行。为了解决这个问题，比较成熟的第三方库通常用C语言实现具体的复杂运算，并将其封装好，供Python调用（之前章节一直使用的scikit-learn就是这样的实现架构，只是这些细节对用户是不可见的，所以容易造成是Python在计算模型的假象）。

正因为如此，自己实现算法时也需要用C语言来封装模型的核心算法，比如隐马尔可夫模型中的Viterbi算法。但问题是C语言比较复杂，实现起来难度较大，有没有比较简单的实现方法呢？答案是使用Cython，它能将大部分Python代码自动地“翻译”成C代码，并将后者封装好，供Python调用。

在随书配套的代码中，用Python和Cython分别实现了Viterbi算法，它们的代码路径分别是viterbipy.py和viterbi.pyx。如果比较两个脚本会发现，绝大部分代码都是一样的，但经过编译⁵后，Cython版的算法比Python版的快10～100倍。有关Cython的具体细节超出了这篇文章的范围，请读者参考其他相关资料。

回到隐马尔可夫模型，讨论上面多次提到的Viterbi算法⁵，该算法负责求解模型预测结果，公式（2）。

$$\hat{Y}=argma{x}_{Y}P(y_0,y_1,...,y_T|X_1,X_2,...,X_T)\text{\hspace{1em}(2)}$$

这个算法的思路是利用动态规划（dynamic programming），将最初的问题转换为相似的子问题来解决。具体地，记$S_T(y_T)=ma{x}_{y_0,...,y_T}P(y_0,...,y_T|X_1,...,X_T)$，也就是说$S_T(y_T)$表示针对自变量$X_1,...,X_T$，在已知第$T$个状态的情况下，所能达到的最大条件概率。数学上可以证明，这个问题可以按如图2所示的方式将其拆解为子问题，这就是Viterbi算法的核心。其中符号$\propto$表示正比于，这样书写是为了避免那些对结果没有影响但又极其繁琐的数学公式，在机器学习领域很常用。至于Viterbi算法实现的具体代码，限于篇幅，在此就不做讨论了。

图2

最后，使用实现好的multinomial HMM模型对中文进行分词，训练模型的文本来自GitHub中的liwenzhu/corpusZh。这份数据是词性标注数据，并没有标准的分词标记。因此在训练模型前，需要对其做数据转换，具体的可参考segmentation_example.py。模型的效果如图3所示，对中文分词的准确度在80%左右。

segmentation_example.py代码片段

def train_model(X, y, lengths):
    """
    训练模型
    """
    vect = CountVectorizer(token_pattern=r"(?u)bw+b")
    XX = vect.fit_transform(X)
    model = MultinomialHMM(alpha=0.01)
    model.fit(XX, y, lengths)
    return vect, model


def chinese_segmentation(data_path):
    """
    对中文分词，并评估模型效果
    """
    train_set, test_set = read_data(data_path, 0.2)
    train_X, train_Y, train_lengths = extract_feature(train_set)
    test_X, test_Y, test_lengths = extract_feature(test_set)
    vect, model = train_model(train_X, train_Y, train_lengths)
    pred = model.predict(vect.transform(test_X), test_lengths)
    print(classification_report([i[0] for i in test_Y], [i[0] for i in pred]))
    # 在Python3中，str不需要decode
    if sys.version_info[0] == 3:
        exampl_str = list("我爱北京天安门")
    else:
        exampl_str = list("我爱北京天安门".decode("utf-8"))
    print_segmentation(exampl_str, model.predict(vect.transform(exampl_str)))

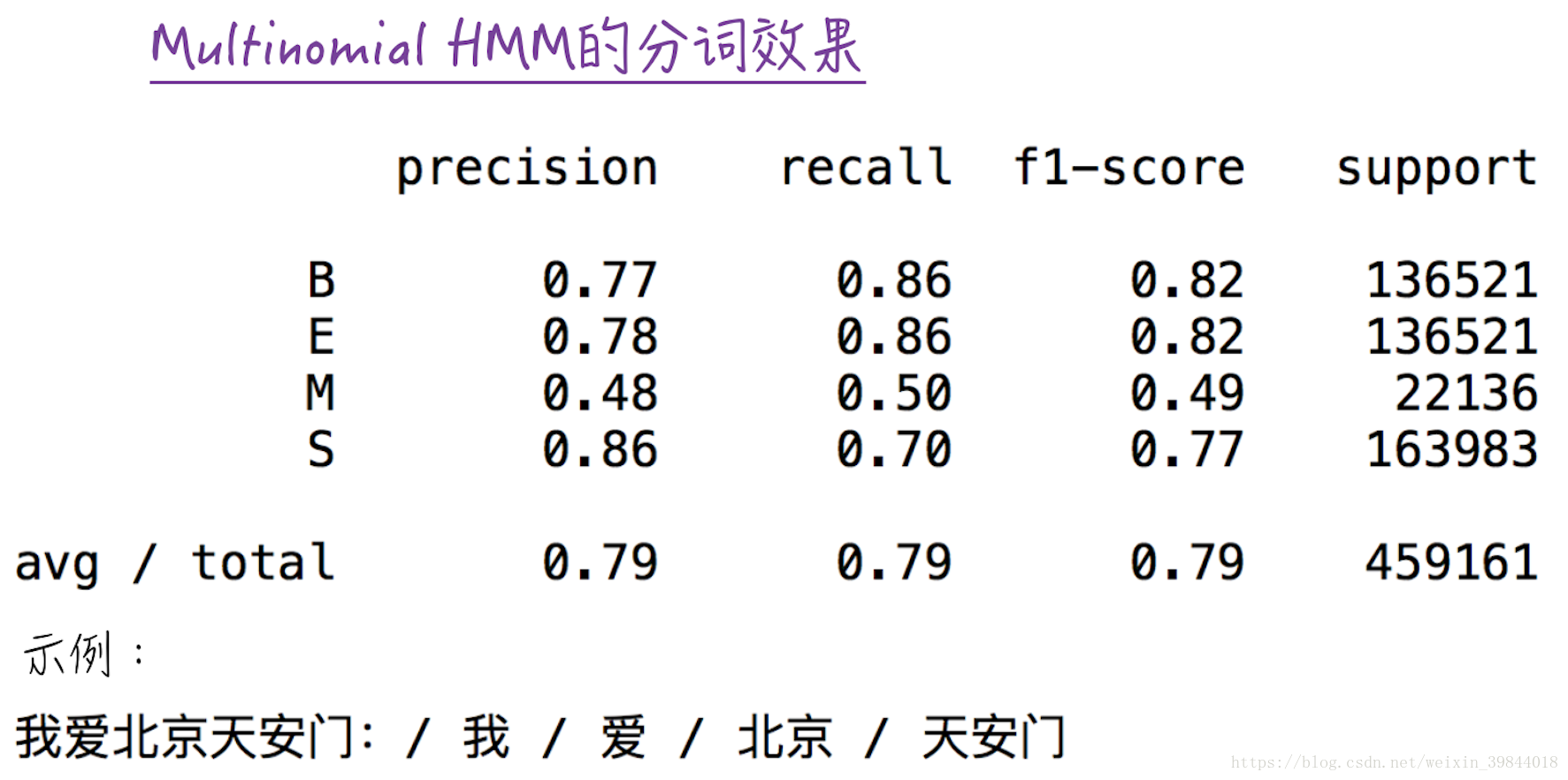图3

三、广告时间

这篇文章的大部分内容参考自我的新书《精通数据科学：从线性回归到深度学习》。

李国杰院士和韩家炜教授在读过此书后，亲自为其作序，欢迎大家购买。

另外，与之相关的免费视频课程请关注这个链接

最后

以上就是舒心枕头为你收集整理的量化投资的利器：隐马尔可夫模型（三）一、中文分词：监督式学习二、中文分词之代码实现三、广告时间的全部内容，希望文章能够帮你解决量化投资的利器：隐马尔可夫模型（三）一、中文分词：监督式学习二、中文分词之代码实现三、广告时间所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。