F - Radio Stations（2-SAT 线段树优化建图）

original link - http://codeforces.com/contest/1215/problem/F

题意：

有$n$个点，$m$个要求：$(x,y)$中至少选择一个点，$k$个冲突：$(x,y)$不能同时选择。

每个点有可行区间$[L_i,R_i]$，要求存在一个$f$，对于所有选择的点$i$，$L_i\le f\le R_i$。

解析：

$2-SAT$裸题。

至少选一个：$\neg x\to y,\neg y\to x$
不能同时选：$x\to \neg y,y\to \neg x$

考虑可行区间，对于$[L_i,R_i]$，显然选择了$i$，对于$j(L_j>R_{i}or{R}_j<L_i)$的不能选，那么分别按左端点和右端点排序后，线段树优化区间建图一下搞定。

空间卡的比较紧，所以很多次$MLE$了。数组写在结构体里面，越界后报的竟然是$TLE$。可能改了其他变量的地址吧。

看了其他人的做法，用类似前缀的思想，维护一条虚链。以右边为例，连向的区间的右端点一定是$n$，所以可以这么建图：

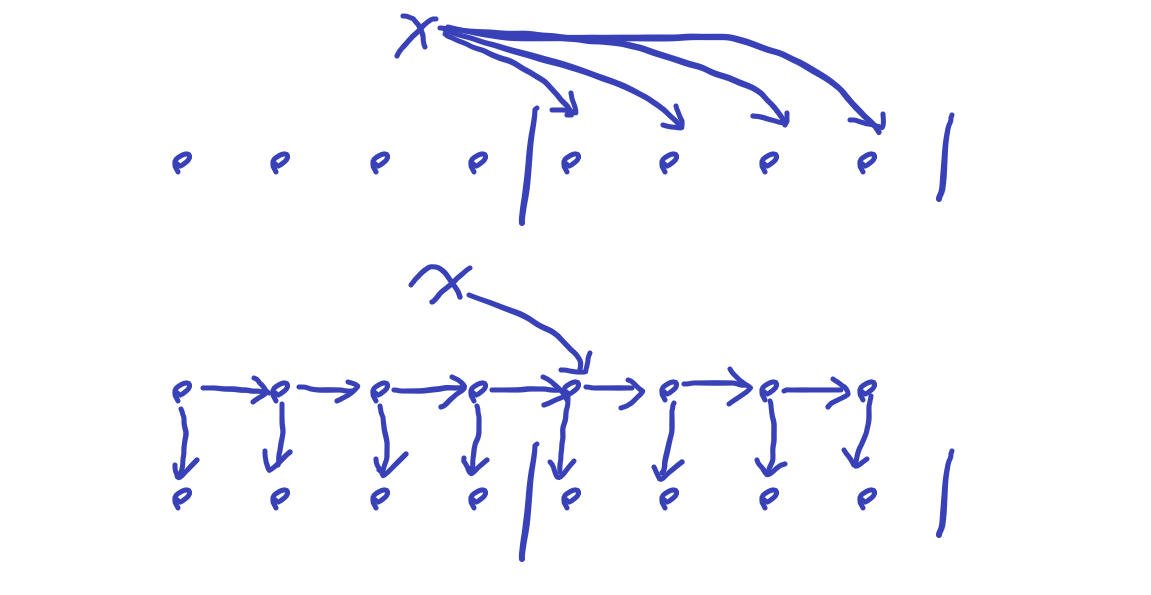
空间复杂度就很优秀了。

代码：

/*
 *  Author : Jk_Chen
 *    Date : 2019-09-18-18.54.43
 */
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define rep(i,a,b) for(int i=(int)(a);i<=(int)(b);i++)
#define per(i,a,b) for(int i=(int)(a);i>=(int)(b);i--)
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define pill pair<int, int>
#define fi first
#define se second
#define debug(x) cerr<<#x<<" = "<<x<<'n';
const LL mod=1e9+7;
const int maxn=4e5+9,maxm=1e7+9,N=2e6+9;
LL rd(){ LL ans=0; char last=' ',ch=getchar();
    while(!(ch>='0' && ch<='9'))last=ch,ch=getchar();
    while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans; return ans;
}
/*_________________________________________________________begin*/
int pid;
int c[maxn],nc[maxn];
 
struct SCC {
    SCC() {
        init();
    }
    int ct=0;
    // edge
    int head[maxm],to[maxm],nex[maxm],now;
    void add(int a,int b) {
        nex[++now]=head[a];
        head[a]=now;
        to[now]=b;
    }
    // scc
    int low[N],dfn[N],scc[N],Idfs,Iscc;
    stack<int>sta;
    bool in[N];
    // init
    void init() {
        memset(head,0,sizeof head);
        now=0;
        memset(dfn,0,sizeof dfn);
        memset(in,0,sizeof in);
        Idfs=Iscc=0;
        while(!sta.empty())
            sta.pop();
    }
    // deal
    void tarjan(int p) {
        low[p]=dfn[p]=++Idfs;
        sta.push(p);
        in[p]=1;
        for(int i=head[p]; i; i=nex[i]) {
            int q=to[i];
            if(!dfn[q])
                tarjan(q),low[p]=min(low[p],low[q]);
            else if(in[q])
                low[p]=min(low[p],dfn[q]);
        }
        if(low[p]==dfn[p]) {
            ++Iscc;
            while(1) {
                int q=sta.top();
                sta.pop();
                scc[q]=Iscc;
                in[q]=0;
                if(p==q)
                    break;
            }
        }
    }
} E;
 
struct node{
    int l,r,id;
    bool operator==(const node&A)const{return r==A.r; }
}e[maxn];
int l[maxn],r[maxn];
bool cmpl(node a,node b){return a.l<b.l;}
bool cmpr(node a,node b){return a.r<b.r;}
 
int trl[maxn<<2],trr[maxn<<2];
#define ls (rt<<1)
#define rs (rt<<1|1)
#define mid (l+r>>1)
void build(int *tr,int rt,int l,int r){
    if(l==r){
        tr[rt]=nc[e[l].id];
        return;
    }
    tr[rt]=++pid;
    build(tr,ls,l,mid);
    build(tr,rs,mid+1,r);
    E.add(tr[rt],tr[ls]);
    E.add(tr[rt],tr[rs]);
}
void add(int u,int *tr,int rt,int l,int r,int L,int R){
    if(l>=L&&r<=R){
        E.add(u,tr[rt]);
        return;
    }
    if(L<=mid){
        add(u,tr,ls,l,mid,L,R);
    }
    if(R>mid){
        add(u,tr,rs,mid+1,r,L,R);
    }
}
 
int main(){
    int _=rd(),n=rd(),__=rd(),___=rd();
    rep(i,1,n)c[i]=++pid,nc[i]=++pid;
    rep(i,1,_){
        int a=rd(),b=rd();
        E.add(nc[a],c[b]);
        E.add(nc[b],c[a]);
    }
    rep(i,1,n){
        e[i].l=rd(),e[i].r=rd(),e[i].id=i;
        l[i]=e[i].l,r[i]=e[i].r;
    }
    sort(e+1,e+1+n,cmpl);
    build(trl,1,1,n);
    rep(i,1,n){
        node tmp;tmp.l=r[i];
        int pos=upper_bound(e+1,e+1+n,tmp,cmpl)-e;
        if(pos<=n){
            add(c[i],trl,1,1,n,pos,n);
        }
    }
    sort(e+1,e+1+n,cmpr);
    build(trr,1,1,n);
    rep(i,1,n){
        node tmp;tmp.r=l[i];
        int pos=lower_bound(e+1,e+1+n,tmp,cmpr)-e;
        if(pos>1){
            add(c[i],trr,1,1,n,1,pos-1);
        }
    }
 
    rep(i,1,___){
        int x=rd(),y=rd();
        E.add(c[x],nc[y]);
        E.add(c[y],nc[x]);
    }
 
    rep(i,1,pid){
        if(!E.dfn[i])E.tarjan(i);
    }
 
    int ans=0,L=1,R=1e9;
    rep(i,1,n){
        if(E.scc[c[i]]==E.scc[nc[i]]){
            printf("-1n");exit(0);
        }
        if(E.scc[c[i]]<E.scc[nc[i]])c[i]=-1,ans++,L=max(L,l[i]),R=min(R,r[i]);
        else nc[i]=-1;
    }
    printf("%d %dn",ans,L);
    rep(i,1,n)if(c[i]+1==0)printf("%d ",i);
    puts("");
    return 0;
}

最后

以上就是酷炫吐司为你收集整理的F - Radio Stations（2-SAT 线段树优化建图）的全部内容，希望文章能够帮你解决F - Radio Stations（2-SAT 线段树优化建图）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。