1. BSM模型的假定

• 1.标的物价格服从几何布朗运动
• 2.允许做空，且可以完全运用做空所获得的资金
• 3.无交易费用、无税收费用，且可以无限分割
• 4.在期权期限内，标的物无期间收入
• 5.市场不存在无风险套利机会
• 6.证券交易是连续进行的
• 7.短期无风险利率是一个常数

BSM模型可由如下微分方程推导：

$$\frac{\partial f}{\partial t}+rs\frac{\partial f}{\partial S}+\frac{1}{2}\frac{{\partial }^{2}f}{\partial S^2}{\sigma }^2{S}^2=rf$$

上式中，$f$ 表示期权价格，$S$ 表示标的物的价格，$r$ 表示连续复利的无风险收益率，$\sigma$ 表示标的物收益率的波动率，$t$ 表示时间变量。上述微分方程的解就是欧式看涨期权的定价公式，其求解过程可以参考这篇文章。

欧式看涨期权的定价公式：

$$c=S_{0}N(d_1)-K{e}^{-rT}N(d_2)$$
其中：$N(x)$ 表示标准正态分布的累积分布函数

由 put-call parity 关系式可推出/欧式看跌期权的定价公式：

$$c+K{e}^{-rT}=p+S_0==>$$

$$p=K{e}^{-rT}N(-d_2)-S_{0}N(-d_1)$$

其中：

$$d_1=\frac{ln(\frac{S_0}{K})+(r+{\sigma }^2/2)T}{\sigma \sqrt{T}}$$

$$d_2=\frac{ln(\frac{S_0}{K})+(r-{\sigma }^2/2)T}{\sigma \sqrt{T}}=d_1-\sigma \sqrt{T}$$

利用Python构建欧式看涨、看跌期权的定价公式

#call的计算
def call_BS(S,K,sigma,r,T):
    import numpy as np
    from scipy.stats import norm
    d1 = (np.log(S/K)+(r+sigma**2/2)*T)/(sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return S*norm.cdf(d1) - K*np.exp(-r*T)*norm.cdf(d2)
#put的计算
def put_BS(S,K,sigma,r,T):
    import numpy as np
    from scipy.stats import norm
    d1 = (np.log(S/K)+(r+sigma**2/2)*T)/(sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return K*np.exp(-r*T)*norm.cdf(-d2) - S*norm.cdf(-d1)

call = call_BS(S = 5.29,K=6,sigma=0.24,r=0.04,T=0.5)
put = put_BS(S = 5.29,K=6,sigma=0.24,r=0.04,T=0.5)
print('看涨期权的价格：',round(call,4))
print('看跌期权的价格：',round(put,4))
看涨期权的价格： 0.1532
看跌期权的价格： 0.7443

2. 期权价格与相关变量的关系

2.1 期权价格与标的物（S）价格的关系

运用BSM模型的期权定价公式，利用Python程序模拟S与期权价格的关系

# 标的价格的变动
S_list = np.linspace(5,7,100)
call_list1 = call_BS(S = S_list,K=6,sigma=0.24,r=0.04,T=0.5)
put_list1 = put_BS(S = S_list,K=6,sigma=0.24,r=0.04,T=0.5)

#画图展示
plt.figure(figsize=(8,6))
plt.plot(S_list,call_list1,label='看涨期权')
plt.plot(S_list,put_list1,label='看跌期权')
plt.legend()
plt.grid('True')

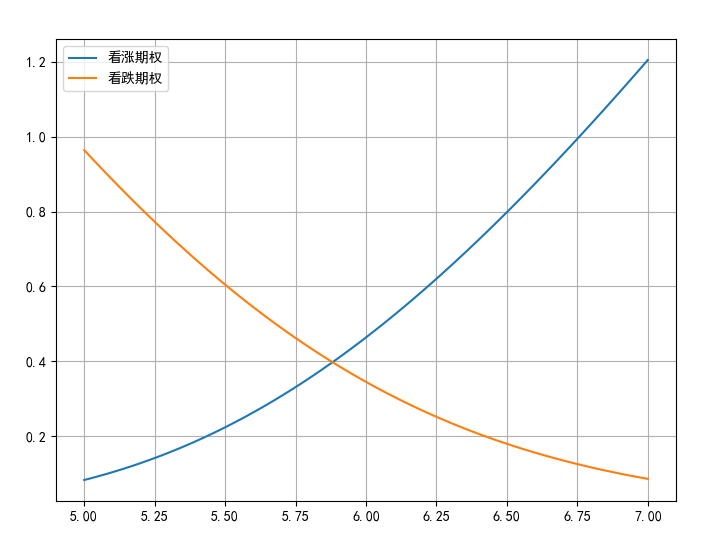
2.2 期权价格与执行价格（K）的关系

运用BSM模型的期权定价公式，利用Python程序模拟K与期权价格的关系

# 执行价格的变动
K_list = np.linspace(5,7,100)
call_list1 = call_BS(S = 5.29,K=K_list,sigma=0.24,r=0.04,T=0.5)
put_list1 = put_BS(S = 5.29,K=K_list,sigma=0.24,r=0.04,T=0.5)

plt.figure(figsize=(8,6))
plt.plot(K_list,call_list1,label='看涨期权')
plt.plot(K_list,put_list1,label='看跌期权')
plt.legend()
plt.grid('True')

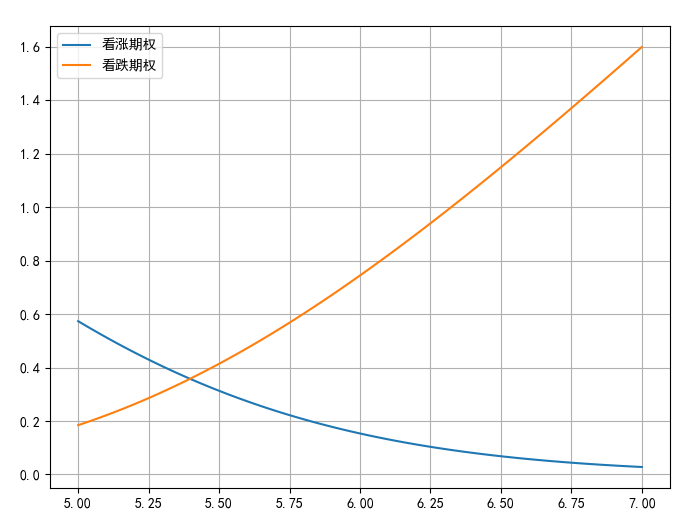
2.3 期权价格与波动率（sigma）的关系

运用BSM模型的期权定价公式，利用Python程序模拟波动率与期权价格的关系

# 波动率的变动
sigma_list = np.linspace(0.05,0.35,100)
call_list1 = call_BS(S = 5.29,K=6,sigma=sigma_list,r=0.04,T=0.5)
put_list1 = put_BS(S = 5.29,K=6,sigma=sigma_list,r=0.04,T=0.5)

plt.figure(figsize=(8,6))
plt.plot(sigma_list,call_list1,label='看涨期权')
plt.plot(sigma_list,put_list1,label='看跌期权')
plt.legend()
plt.grid('True')

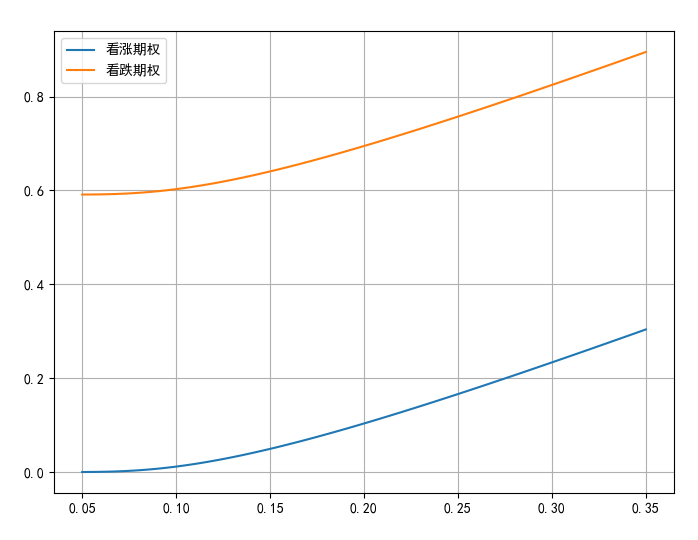
2.4 期权价格与无风险收益率（r）的关系

运用BSM模型的期权定价公式，利用Python程序模拟无风险收益率与期权价格的关系

# 无风险收益率的变动
r_list = np.linspace(0.01,0.1,100)
call_list1 = call_BS(S = 5.29,K=6,sigma=0.24,r=r_list,T=0.5)
put_list1 = put_BS(S = 5.29,K=6,sigma=0.24,r=r_list,T=0.5)

plt.figure(figsize=(8,6))
plt.plot(r_list,call_list1,label='看涨期权')
plt.plot(r_list,put_list1,label='看跌期权')
plt.legend()
plt.grid('True')

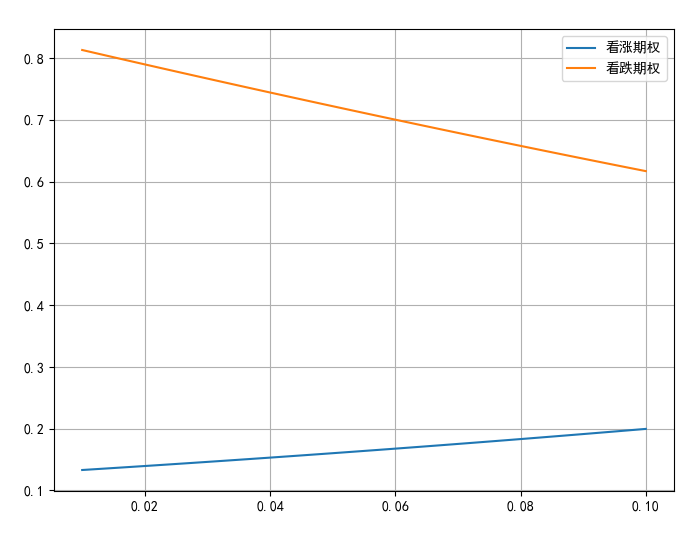
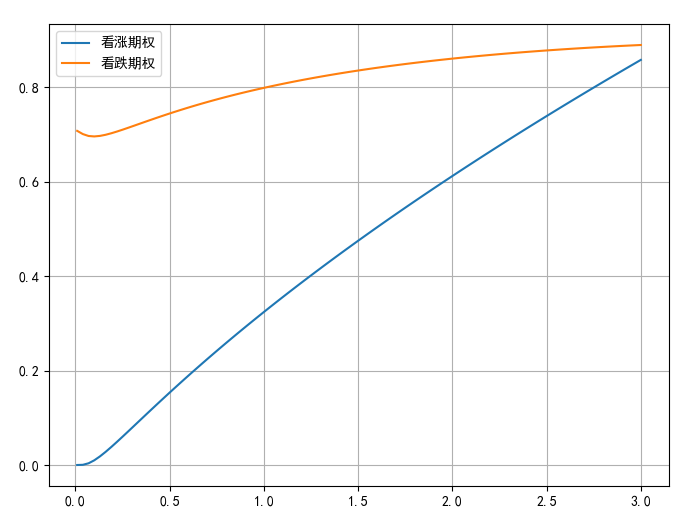
2.5 期权价格与期权剩余期限（t）的关系

运用BSM模型的期权定价公式，利用Python程序模拟无风险收益率与期权价格的关系

# 时间的变动
T_list = np.linspace(0.01,3,100)
call_list1 = call_BS(S = 5.29,K=6,sigma=0.24,r=0.04,T=T_list)
put_list1 = put_BS(S = 5.29,K=6,sigma=0.24,r=0.04,T=T_list)

plt.figure(figsize=(8,6))
plt.plot(T_list,call_list1,label='看涨期权')
plt.plot(T_list,put_list1,label='看跌期权')
plt.legend()
plt.grid('True')

最后

以上就是魁梧哈密瓜为你收集整理的金融分析与风险管理——期权BSM模型1. BSM模型的假定2. 期权价格与相关变量的关系的全部内容，希望文章能够帮你解决金融分析与风险管理——期权BSM模型1. BSM模型的假定2. 期权价格与相关变量的关系所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。