python基于rsa的数字签名实现_Python实现期权定价基于BSM模型

一、BS模型相关的定义、假设和公式

        期权的价格与标的资产价格之间存在非线性关系，且受时间等因素影响，所以期权的定价是一个非常复杂的问题。到了1973年，该定价难题终于得到解答。美国的费希尔•布莱克(Fischer• Black)和马龙•舒尔斯(Myron•Merton)利用随机微分方程等数学工具，建立起Black–Schole模型，也就是我们如今常用的欧式股票期权的定价公式，该公式也成为了期权定价的里程碑。

        首先需要关注的就是模型的假设

1、标的资产的价格服从几何布朗运动

2、在期权有效期内，无风险利率和金融资产收益变量是恒定的；

3、市场无摩擦，即不存在税收和交易成本，所有证券完全可分割；

4、该期权是欧式期权，即在期权到期前不可实施。

5、市场是完全市场，不存在无风险套利机会；

6、证券交易是持续的；

7、投资者能够以无风险利率借贷

        该模型在期权定价历史过程中确实具有里程碑意义，但是其模型的假设很大程度上和实际是有差异的，如标的价格服从对数正态分布，没有考虑标的价格突变情况以及标的波动率变化等(可参考之前分析的股指期货IF的相关的波动率图像走势)

中金所股指期货IF的波动率

逸飞，公众号：围着围巾的小黑Python带你分析股指期货IF

；市场无摩擦的假设也是有待商榷的，实际上市场交易存在多种交易成本，完全市场的假设也是不尽合理 。针对上述的种种限制和约束，后续有各种模型在上面做调整。

        模型的公式

二、用Python实现期权定价

import numpy as np# 关键参数约定和说明St 标的资产的价格K  期权的行权价格t  期权定价或者估值的时间(年为单位)T  期权的到期日时间(年为单位)T-t 期权的剩余到期时间(年为单位)# 按照上述公式中的要求先计算d1的值def d1cal(St, K, t, T, r, sigma):    d1 = (np.log(St / K) + (r + 0.5 * sigma ** 2)* (T - t)) / (sigma * np.sqrt(T - t))    return d1    # 正态分布累积密度函数def N(d):    return st.norm.cdf(d)    # 按照上述公式实现的看涨期权定价公式def BSM_call_value(St,K,t,T,r,sigma):    d1 = d1cal(St, K, t, T, r, sigma)    d2 = d1 - sigma * np.sqrt(T - t)    call_value = St * N(d1) - np.exp(-r * (T - t)) * K * N(d2)    return call_value 

三、期权定价的可视化分析

        基于上述期权定价公式，可以对期权的主要影响参数进行分析，影响期权价格的主要参数有五个St、K、T-t、r、sigma等，我们通过控制变量的方法来依次分析不同的K、T-t、r、sigma等对期权价格的影响。

import numpy as npimport matplotlib as mplimport matplotlib.pyplot as plt

# 保持其他参数不变，行权价K变化def plot_differentK(function):    plt.figure(figsize=(10,8))    points = 100    St = 100.0      K = 100.0      t = 0.0      T = 1.0      r = 0.05      sigma = 0.2      klist = np.linspace(80, 120, points)    vlist = [function(St, K, t, T, r, sigma) for K in klist]    plt.plot(klist, vlist)    plt.grid()    plt.xlabel('strike K')    plt.ylabel('present value')    plot_differentK(BSM_call_value)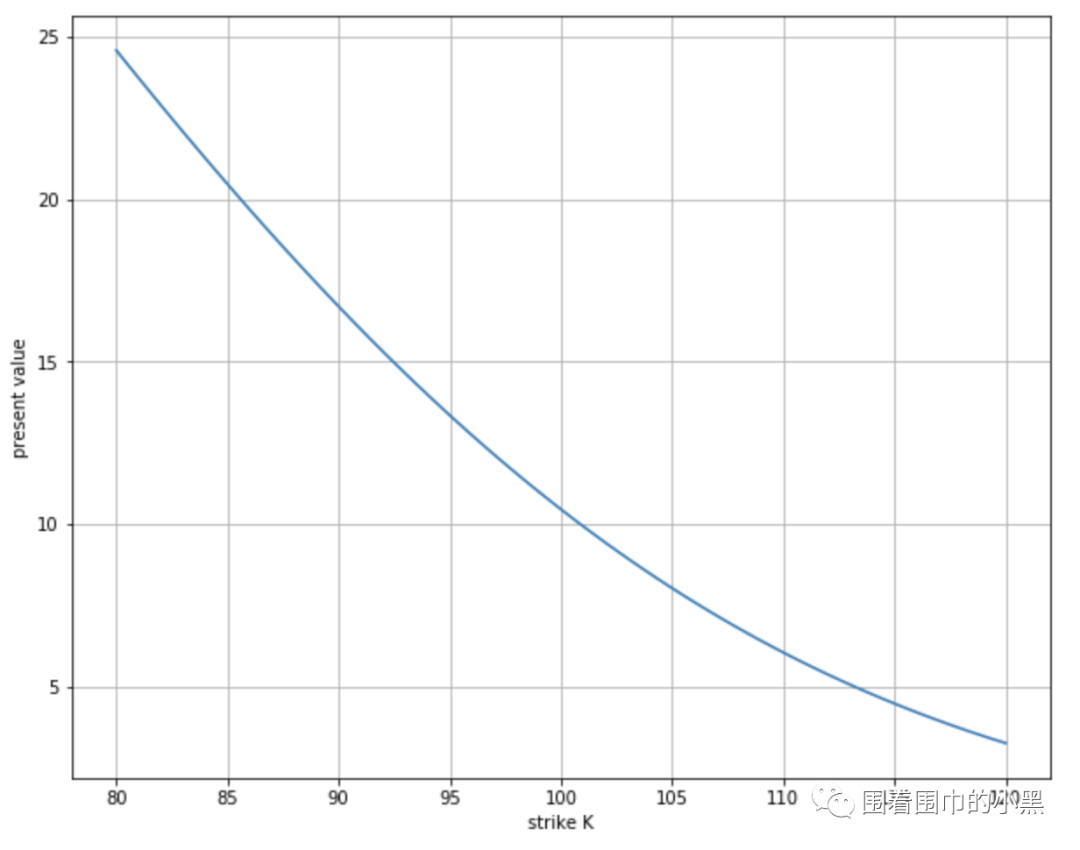

对于看涨期权，行权价越高，期权的价格(价值)越低。

# 保持其他参数不变，剩余到期时间T变化def plot_differentT(function):    plt.figure(figsize=(10,8))    points = 100    St = 100.0      K = 100.0      t = 0.0      T = 1.0      r = 0.05      sigma = 0.2     tlist = np.linspace(0.0001, 1, points)    vlist = [function(St, K, t, T, r, sigma) for T in tlist]    plt.plot(tlist, vlist)    plt.grid(True)    plt.xlabel('maturity T')    plt.ylabel('present value')    plot_differentT(BSM_call_value)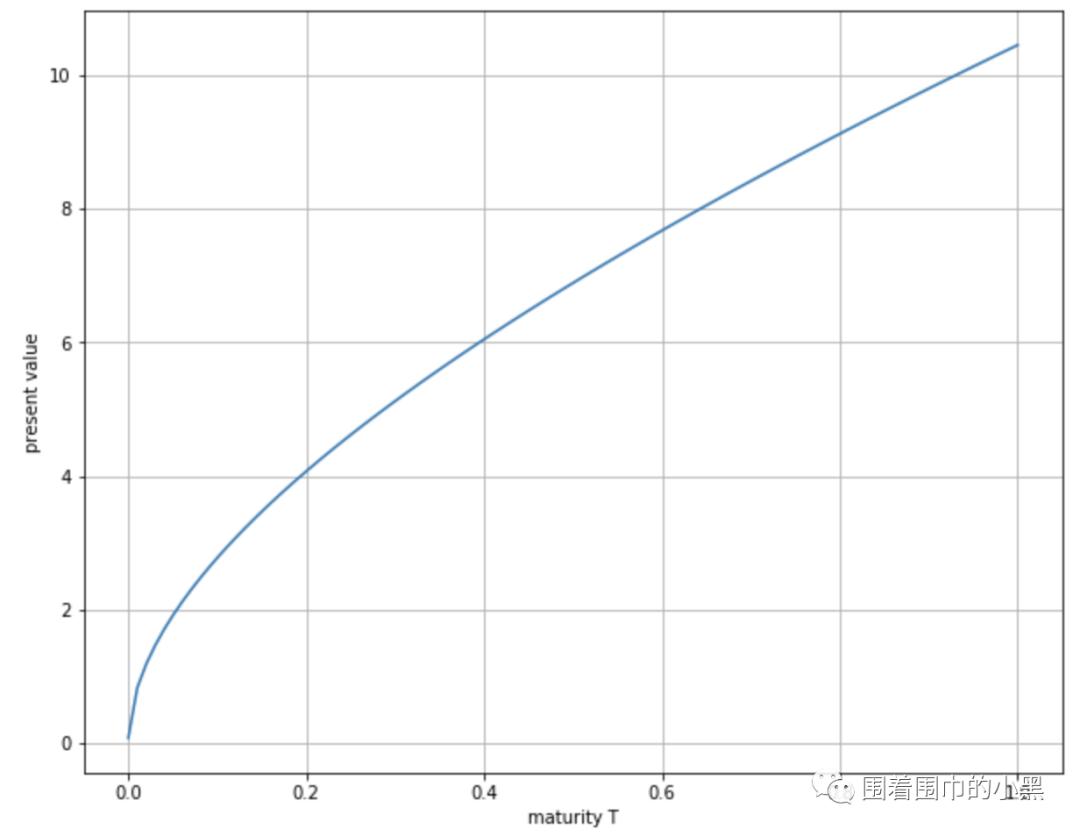

    对于看涨期权，随着到期时间的变大，期权的价格(价值)在上升。

# 保持其他参数不变，无风险利率变化def plot_differentR(function):    plt.figure(figsize=(10,8))    points = 100    St = 100.0      K = 100.0      t = 0.0      T = 1.0      r = 0.05      sigma = 0.2     rlist = np.linspace(0, 0.1, points)    vlist = [function(St, K, t, T, r, sigma) for r in rlist]    plt.plot(rlist, vlist)    plt.grid(True)    plt.xlabel('short rate r')    plt.ylabel('present value')    plot_differentR(BSM_call_value)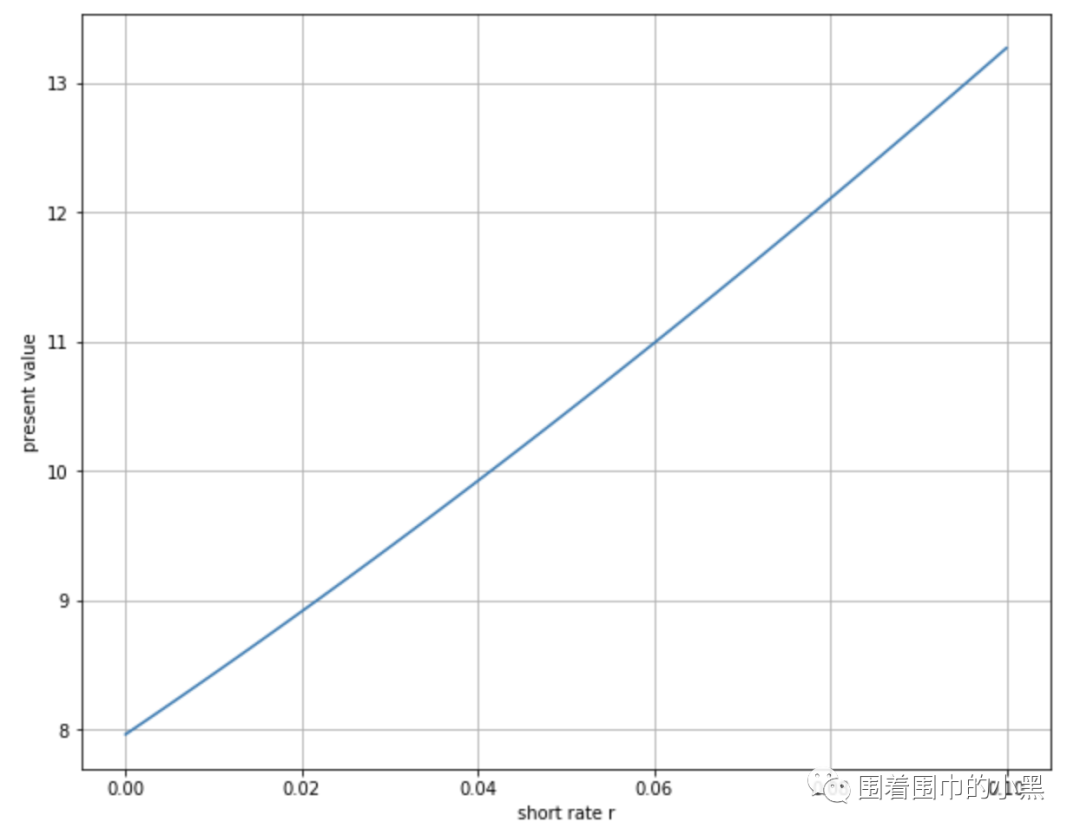

对于看涨期权，随着短期利率的上升，期权的价格(价值)会上升。

# 保持其他参数不变，波动率Sigma变化def plot_differentSigma(function):    plt.figure(figsize=(10,8))    points = 100    St = 100.0      K = 100.0      t = 0.0      T = 1.0      r = 0.05      sigma = 0.2     slist = np.linspace(0.01, 0.5, points)    vlist = [function(St, K, t, T, r, sigma) for sigma in slist]    plt.plot(slist, vlist)    plt.grid(True)    plt.xlabel('volatility sigma')    plt.ylabel('present value')    plot_differentSigma(BSM_call_value)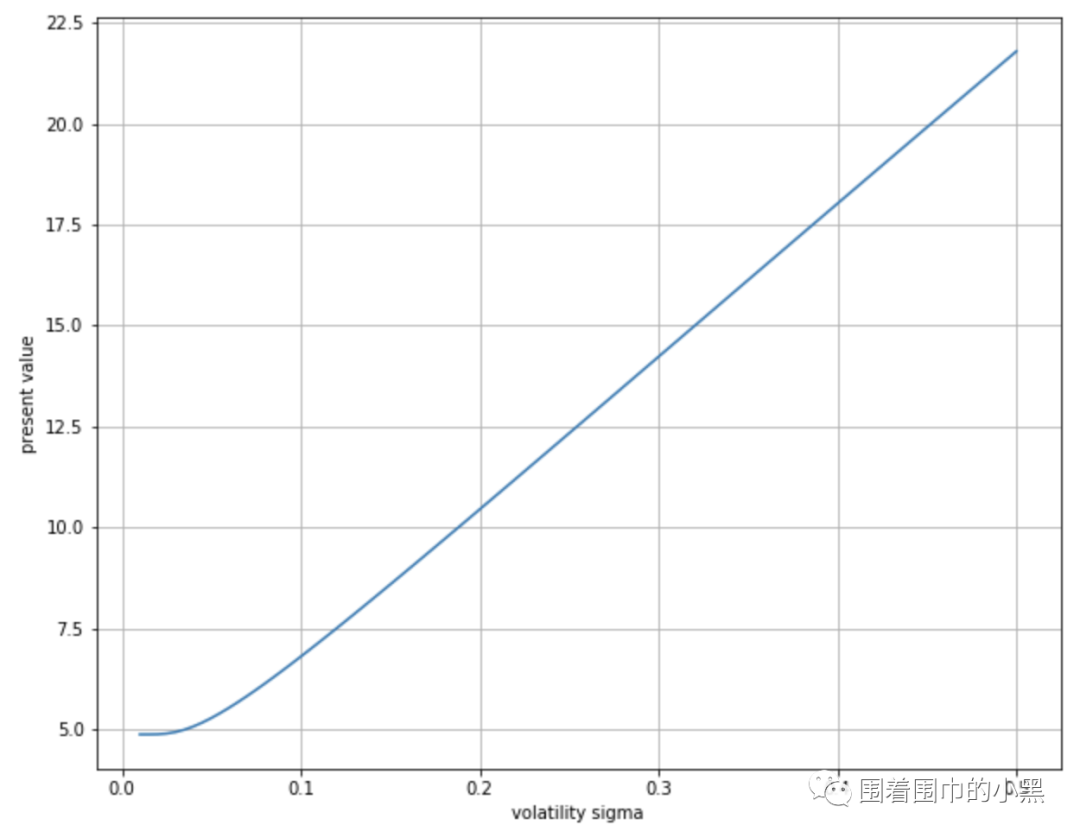

对于看涨期权，随着波动率的上升，期权的价格(价值)也会上升。