分类算法系列--近邻（Nearest Neighbors）

近邻算法可以分为无监督的近邻算法和监督近邻算法。

无监督的近邻算法是很多学习方法的基础：流形学习，谱聚类算法。

监督近邻方法可以分为:分类的近邻算法（针对离散的数据集）和回归的近邻算法（连续值的数据集）

• 分类近邻算法多采用多数表决法，在训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别。
• 回归近邻算法选择平均法，即最近的K个样本的样本输出的平均值作为回归预测值。

近邻算法是一种无参数的算法

近邻算法三要素：k值的选取，距离度量的方式和分类决策规则。

对于分类决策规则，一般都是使用前面提到的多数表决法。重点关注与k值的选择和距离的度量方式。

• 关于k值的选择

k值一般取较小的值，然后通过交叉验证法来选取最优的k值

• 关于距离的度量方式

1.欧式距离（常用）

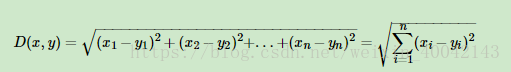
   2. 曼哈顿距离

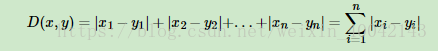
  3.闵可夫斯基距离(Minkowski Distance)

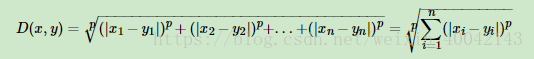
欧式距离是闵可夫斯基距离距离在p=2时的特例，而曼哈顿距离是p=1时的特例。

分类决策规则

多数表决

KNN算法实现

最简单的：线性扫描，计算输入实例与每一个训练实例的距离，然后取出距离最近的k个进行表决。当训练集很大的时候费时。

KD-树

kd tree是一个二叉树，表示对k维空间的一个划分。

注意：KNN中的K代表特征输出类别，KD树中的K代表样本特征的维数。

KD树算法包括三步，第一步是建树，第二部是搜索最近邻，最后一步是预测。

kd树构建

1. 从m个样本的n维特征中，分别计算n个特征的取值的方差，用方差最大的第k维特征nk来作为排序的基准对样本进行排序
2. 选择特征nk的取值的中位数对应的样本作为划分点
3. 对于第k维特征的取值大于等于nk的样本，划入右子树，否则，划入左子树；对于左子树和右子树，我们采用和刚才同样的办法来找方差最大的特征来做更节点，递归的生成KD树。

流程图如下：

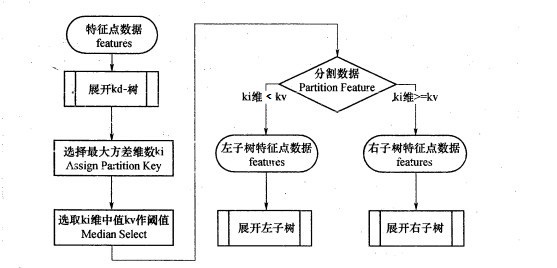
搜索最近邻

对于一个目标点，我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心，以目标点到叶子节点样本实例的距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点，检查另一个子节点包含的超矩形体是否和超球体相交，如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了，我们直接返回父节点的父节点，在另一个子树继续搜索最近邻。当回溯到根节点时，算法结束，此时保存的最近邻节点就是最终的最近邻。

最后

以上就是糟糕苗条为你收集整理的分类算法系列--近邻（Nearest Neighbors）的全部内容，希望文章能够帮你解决分类算法系列--近邻（Nearest Neighbors）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。