脑图

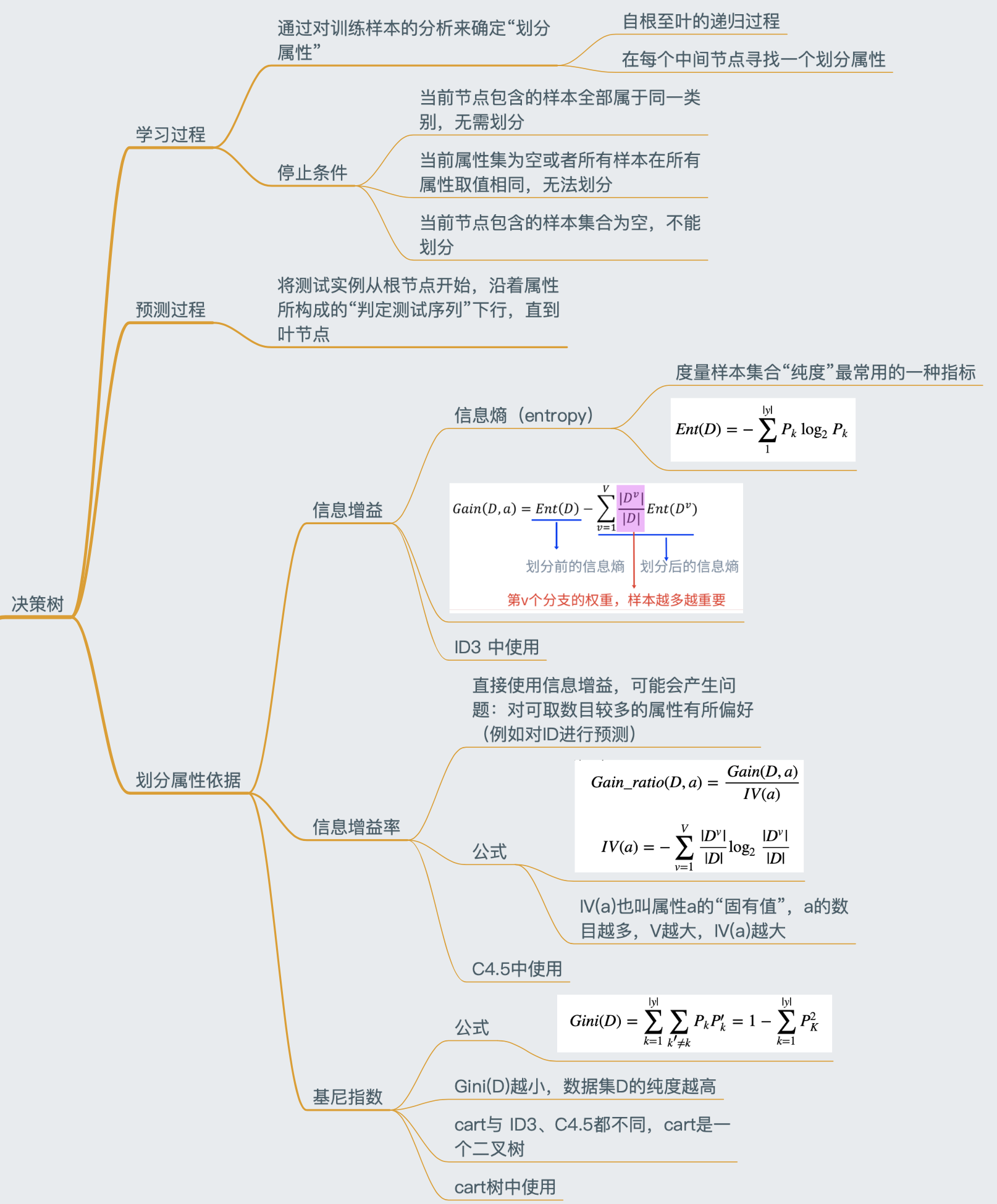
从LR到决策树

总体流程与核心问题

• 总体流程 : 分而治之 divide-and-conquer
  • 自根至叶的递归过程
  • 在每个中间节点寻找一个“划分”（split or test）属性
• 三种停止条件：
  • 当前节点包含的样本全属于同一类别，无需划分（节点的一票否决权）
  • 当前属性集为空，或者所有样本在所有属性上取值相同，无法划分（所有属性都一样，但是最后的结果又不同，无法区分了）
  • 当前节点包含的样本集合为空，不能划分

下图摘自西瓜书，红底色文字就是决策树算法的核心：怎么选？

熵、信息增益、信息增益率

熵

信息熵（entropy）是度量样本集合“纯度”最常用的一种指标，假定当前样本集合D中第k类样本所占比例为 $p_k$, 则D的信息熵定义为：
$$Ent(D)=-\sum _1^{|y|}{P}_k{\log }_2{P}_k$$

• 这里的 |y| 代表类别数量
• Ent(D)越小，则D的纯度越高
• Ent(D)的最小值时0，最大值是 ${\log }_2|y|$

信息增益直接以信息熵为基础，计算当前划分对信息熵所造成的变化

最佳划分属性选择：信息增益（ID3）

信息增益 information gain：ID3中使用

【实例：西瓜书判断西瓜熟度】

最佳划分属性选择：信息增益率(C4.5)

使用信息增益有什么问题：对可取值数目较多的属性有所偏好（例如使用学号进行成绩区分，每一个学号下只有一个样本）

下面我们引入一个概念：信息增益率
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中，$$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}{\log }_2\frac{|D^v|}{|D|}$$
IV(a)也叫属性a的“固有值”，a的数目越多，V越大，IV(a)越大，

1.2.4 最佳划分属性选择：基尼指数

分类与回归树 Cart - Classification and Rgression 中使用

定义基尼指数 Gini index ：
$$Gini(D)=\sum _{k=1}^{|y|}\sum _{k^{\prime }\ne k}{P}_k{P}_k^{\prime }=1-\sum _{k=1}^{|y|}{P}_K^2$$

Gini(D)越小，数据集D的纯度越高

属性a的基尼指数：
$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$

在候选属性的集合中，选取使得划分后基尼指数最小的属性

cart与 ID3、C4.5都不同，cart是一个二叉树

基尼指数本质上与信息熵相同，推导：

写作不易，求电费

最后

以上就是深情戒指为你收集整理的【机器学习】决策树与树模型集成01-决策树脑图从LR到决策树写作不易，求电费的全部内容，希望文章能够帮你解决【机器学习】决策树与树模型集成01-决策树脑图从LR到决策树写作不易，求电费所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。