Hinge loss Hinge loss

50 阅读 0 评论 33 点赞

我是靠谱客的博主积极香水，最近开发中收集的这篇文章主要介绍Hinge loss Hinge loss，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Hinge loss

In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs).^[1] For an intended output t = ±1 and a classifier score y, the hinge loss of the prediction y is defined as

$ell(y) = max(0, 1-t cdot y)$

Note that y should be the "raw" output of the SVM's decision function, not the predicted class label. E.g., in linear SVMs, $y = mathbf{w} cdot mathbf{x} + b$ .

It can be seen that when $t$ and $y$ have the same sign (meaning $y$ predicts the right class) and $y ge 1$ , $ell(y) = 0$ (one-sided error), but when they have opposite sign, $ell(y)$ increases linearly with $y$ .

Extensions[edit]

While SVMs are commonly extended to multiclass classification in a one-vs.-all or one-vs.-one fashion,^[2] there exists a "true" multiclass version of the hinge loss due to Crammer and Singer,^[3] defined for a linear classifier as^[4]

$ell(y) = max(0, 1 + max_{y ne t} mathbf{w}_y mathbf{x} - mathbf{w}_t mathbf{x})$

In structured prediction, the hinge loss can be further extended to structured output spaces. Structured SVMs use the following variant, where w denotes the SVM's parameters, φ the joint feature function, and Δ the Hamming loss:^[5]

$begin{align}ell(mathbf{y}) & = delta(mathbf{y}, mathbf{t}) + langle mathbf{w}, phi(mathbf{x}, mathbf{y}) rangle - langle mathbf{w}, phi(mathbf{x}, mathbf{t}) rangle \ & = max_{y in mathcal{y}} left( delta(mathbf{y}, mathbf{t} + langle mathbf{w}, phi(mathbf{x}, mathbf{y}) rangle) right) - langle mathbf{w}, phi(mathbf{x}, mathbf{t}) rangleend{align}$

Optimization[edit]

The hinge loss is a convex function, so many of the usual convex optimizers used in machine learning can work with it. It is not differentiable, but has asubgradient with respect to model parameters 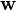$mathbf{w}$ of a linear SVM with score function 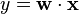$y = mathbf{w} cdot mathbf{x}$ that is given by

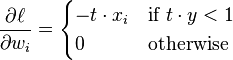
$frac{partialell}{partial w_i} = begin{cases} -t cdot x_i & text{if } t cdot y < 1 \ 0 & text{otherwise} end{cases}$

https://groups.google.com/forum/#!topic/theano-users/Y8lQqOzXC0A

由于hinge loss不是处处可导的。

Quick question: since hinge loss isn't differentiable, are there any standard practices / suggestions on how to implement a loss function
that might incorporate a max{0,something} in theano that can still be automatically differentiable? I'm thinking maybe evaluate a scalar
cost on the penultimate layer of the network and *hack* a loss function to arrive at a scalar loss?

I know of two differentiable functions that approximate the behavior
of max{0,x}. One is:

{log(1 + e^(x*N)) / N} -> max{0,x} as N->inf

The other is the activation function Geoff Hinton uses for rectified
linear units.

As a side note, in case anyone is curious where the crossover is:

log(1 + e^(x)) is the anti-derivative of the logistic function,
whereas RLUs are a form of integration that when carried out
infinitely will asymptotically approach the same behavior as log(1 +
e^(x)). That's the link between them.

-Brian

Thanks Brian, I actually ended up switching to a log-loss...

log(1 + exp( (m - x) * N)) / (m * N)

as an approximation to the margin loss I wanted,

max(0, m - x)

and everything's looking good / behaving nicely.

-Eric