用帖子记录一下,防止忘记
原文链接:Real-Time Loop Closure in 2D LIDAR SLAM
文章结构:
- ABSTRACT
- INTRODUCTION
- RELATED WORK
- SYSTEM OVERVIEW
- LOCAL 2D SLAM
- CLOSING LOOPS
- EXPERIMENTAL RESULTS
- CONCLUSIONS
ABSTRACT
- Lidar传感器和SLAM方法是获取平面竣工图的有效方法
- 实时生成的平面图需要在有限的计算资源下获取。
- Cartographer方法构建的地图分辨率为5cm(一个格边长为5cm),可以实时构图,可以进行回环检测
- 为了加速回环检测过程,满足Cartographer实时建图的要求,采用分枝定界的方法。
- 实验表明,Cartographer方法具备竞争力
ⅠINTRODUCTION
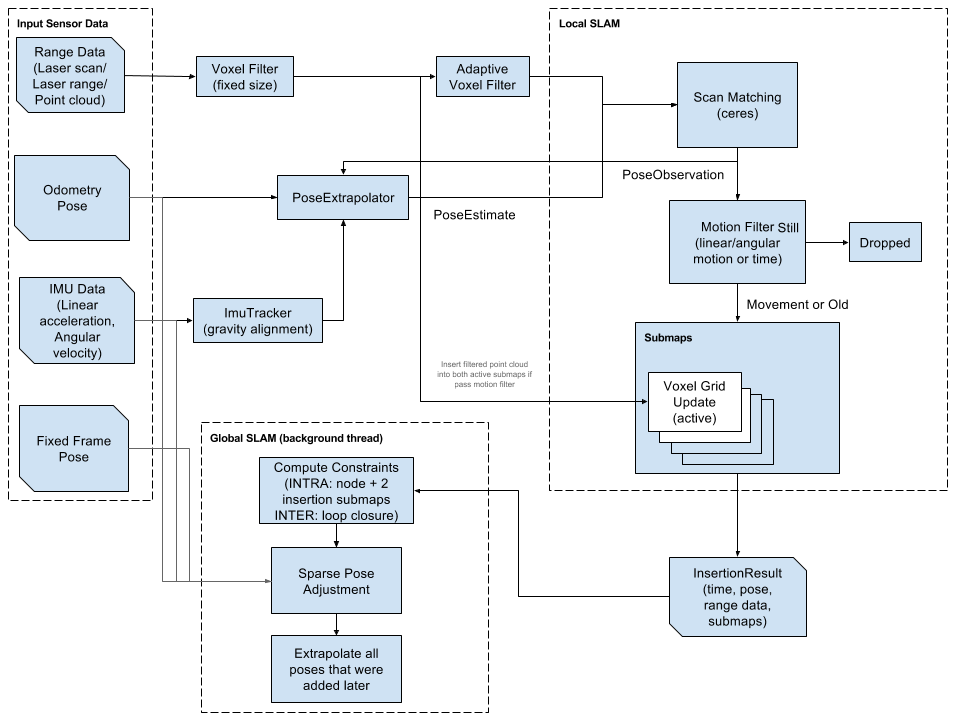
分析其流程图:
- 1、激光输入——>体素滤波(VoxelFilter)——>自适应体速滤波(Adaptive VoxelFilter)
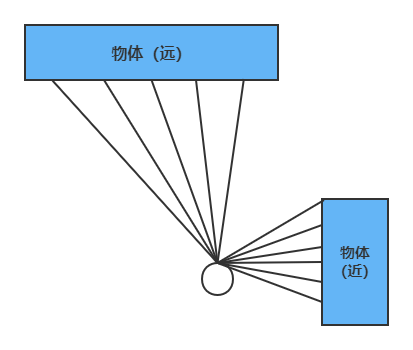
这里解释一下滤波作用:激光雷达(例如常见单线激光雷达)发射出的测距激光为等角度分布,这就会导致照射到近处的激光点分布密集,而照射到远处的激光点分布稀疏。近处,密度大的激光点会需要额外的内存,还需要额外的运算资源进行下一步配准,但这部分多余的激光点对定位精度提升很微弱(或者说)。因此,为了避免这些无效点对于资源的消耗,需要滤除一部分的激光点。
2、IMU数据输入——>IMU Track(使用来自imu的角速度+加速度用于跟踪pose的orientation)——>结合里程计、Scan matching实现对激光数据进行插值
3、里程计数据输入——>
4、Local SLAM:
Ⅱ RELATED WORK
前端配准方法:
| scan to scan | scan to map(本文) | Pixel-accurate scan |
|---|---|---|
| ICP、PL-ICP | CSM(相关匹配-粗配准) | 精度高、计算量大 |
| 累积误差明显 | 梯度优化(精配准) | |
| 不适应大场景 | G-N方法需良好初始值(高频Lidar、IMU) |
处理剩余局部误差方法:
| 粒子滤波 | 图优化(本文) |
|---|---|
| 粒子滤波随地图变大变成资源密集型 | 构建节点(位姿)和边(约束)之间的关系 |
Ⅲ SYSTEM OVERVIEW
- Cartographer获取平面竣工图利用配备传感器的背包,可以生成一张分辨率r = 5cm 的二维栅格地图。
- 软实时约束(即不是真正意义上的实时),因为还要后端优化过程,即使离线跑bag包,在数据播放完时,也还有一段时间用来进行优化过程。
- 利用分枝定界加速、预计算栅格
Ⅳ LOCAL 2D SLAM
- Cartographer结合了局部和全局的2D SLAM方法,两种方法都能够优化Lidar观测到的位姿( ξ x xi_x ξx, ξ y xi_y ξy, ξ θ xi_theta ξθ)包含了平移变换(x,y)和旋转变换 ξ θ xi_theta ξθ
- 子图匹配(scan to submap)的过程即一帧一帧数据与子图扫描对齐迭代过程,扫描匹配随着时间累计误差,这些误差在全局过程中去消除。
A.Scans
子图的构造是反复对齐帧和Submap坐标系的过程。假设扫描原点0
∈
in
∈R2,把激光雷达的扫描点写入H = {
h
k
{h_k}
hk} , k = 1,2……K。
位姿
ξ
xi
ξ表示为刚体变换变换矩阵
T
ξ
T_xi
Tξ,将每一帧激光点从scan坐标系转换到submap坐标系下。
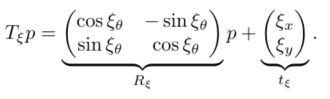
B.Submap
关于概率栅格地图,参考:https://zhuanlan.zhihu.com/p/21738718
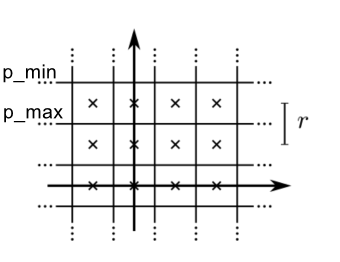 | 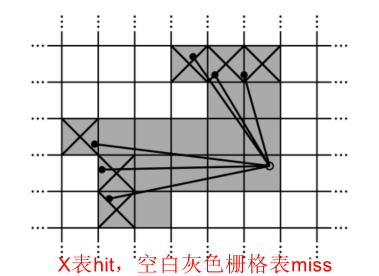 |
在扫描过程中,被激光击中(hit)的栅格我们将其加入到hit set中,对于一束激光中未命中的栅格我们将其加入到miss set中。如果这些栅格没有被观测过,会被分配一个概率
p
h
i
t
p_{hit}
phit和
p
m
i
s
s
p_{miss}
pmiss。如果有栅格x已经被观测过
,我们将其odds更新为
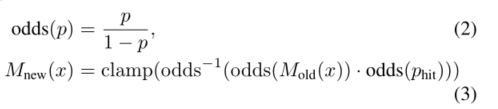
其中,clamp函数为区间限定函数。
C.Ceres scan matching(CSM)
将一帧激光数据插入到submap之前,使用基于ceres的扫描匹配优化当前帧的位姿
ξ
xi
ξ。扫描匹配器负责找到一个位姿,使submap中扫描点概率最大化,在这转换成一个非线性最小二乘法问题。
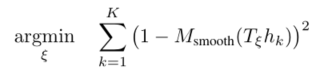
这里T是将hk从扫描坐标转换到子地图坐标的变换矩阵。函数
M
s
m
o
o
t
h
M_{smooth}
Msmooth函数是局部submap中概率值的光滑版本,使用双三次插值。只关心区间【0,1】之间的值,要使得整体最小,即M取得最大值。
光滑函数优化的概率值比起分辨率能够提供更好的精度,需要IMU数据提供一个良好的初始值。
关于这部分优化问题的求解,具体细节如下:
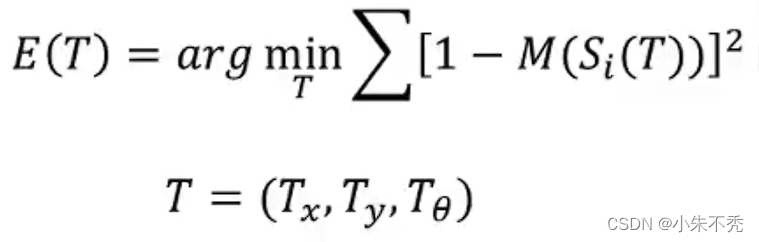
假设第
i
i
i个激光点的坐标是
p
i
p_i
pi = (
p
i
x
p_{ix}
pix,
p
i
y
p_{iy}
piy)表示第
i
i
i个激光点的坐标。通过S函数坐标转换成世界坐标(map):
S
i
(
T
)
=
[
cos
T
θ
−
sin
T
θ
T
x
sin
T
θ
cos
T
θ
T
y
0
0
1
]
[
p
i
x
p
i
y
1
]
S_ileft( T right) =left[ begin{matrix} cos T_{theta}& -sin T_{theta}& T_x\ sin T_{theta}& cos T_{theta}& T_y\ 0& 0& 1\ end{matrix} right] left[ begin{array}{c} p_{ix}\ p_{iy}\ 1\ end{array} right]
Si(T)=⎣⎡cosTθsinTθ0−sinTθcosTθ0TxTy1⎦⎤⎣⎡pixpiy1⎦⎤
M(
S
i
(
T
)
S_i(T)
Si(T))为非线性函数,因此进行一阶泰勒展开,得:
E
(
T
+
Δ
T
)
=
a
r
g
min
Δ
T
Σ
[
1
−
M
(
S
i
(
T
)
)
−
∇
M
(
S
i
(
T
)
)
∂
S
i
(
T
)
∂
T
Δ
T
]
2
Eleft( T+varDelta T right) ,,=,,arg,,underset{varDelta T}{min}varSigma left[ 1-Mleft( S_ileft( T right) right) -nabla Mleft( S_ileft( T right) right) frac{partial S_ileft( T right)}{partial T}varDelta T right] ^2
E(T+ΔT)=argΔTminΣ[1−M(Si(T))−∇M(Si(T))∂T∂Si(T)ΔT]2其中
∇
M
(
S
i
(
T
)
)
=
∂
M
(
S
i
(
T
)
)
S
i
(
T
)
nabla Mleft( S_ileft( T right) right) ,,=,,frac{partial Mleft( S_ileft( T right) right)}{S_ileft( T right)}
∇M(Si(T))=Si(T)∂M(Si(T))转换成了线性系统,求其对
Δ
T
varDelta T
ΔT的导数,并且令其等于0:
Σ
[
∇
M
(
S
i
(
T
)
)
∂
S
i
(
T
)
∂
T
]
T
[
1
−
M
(
S
i
(
T
)
)
−
∇
M
(
S
i
(
T
)
)
∂
S
i
(
T
)
∂
T
Δ
T
]
=
0
varSigma left[ nabla Mleft( S_ileft( T right) right) frac{partial S_ileft( T right)}{partial T} right] ^Tleft[ 1-Mleft( S_ileft( T right) right) -nabla Mleft( S_ileft( T right) right) frac{partial S_ileft( T right)}{partial T}varDelta T right] ,,=,,0
Σ[∇M(Si(T))∂T∂Si(T)]T[1−M(Si(T))−∇M(Si(T))∂T∂Si(T)ΔT]=0
求解上式可以得到
Δ
T
varDelta T
ΔT,令T= T +
Δ
T
varDelta T
ΔT,不断迭代即可。
最终得到的
Δ
T
=
H
−
1
Σ
[
∇
M
S
i
(
T
)
∂
S
i
(
T
)
∂
T
]
T
[
1
−
M
(
S
i
(
T
)
)
]
varDelta T,,=,,H^{-1}varSigma left[ nabla MS_ileft( T right) frac{partial S_ileft( T right)}{partial T} right] ^Tleft[ 1-Mleft( S_ileft( T right) right) right]
ΔT=H−1Σ[∇MSi(T)∂T∂Si(T)]T[1−M(Si(T))]
H
=
Σ
[
∇
M
(
S
i
(
T
)
)
∂
S
i
(
T
)
∂
T
]
T
[
∇
M
(
S
i
(
T
)
)
∂
S
i
(
T
)
∂
T
]
H,,=,,varSigma left[ nabla Mleft( S_ileft( T right) right) frac{partial S_ileft( T right)}{partial T} right] ^Tleft[ nabla Mleft( S_ileft( T right) right) frac{partial S_ileft( T right)}{partial T} right]
H=Σ[∇M(Si(T))∂T∂Si(T)]T[∇M(Si(T))∂T∂Si(T)]
Δ
T
varDelta T
ΔT中所有的量都已经知道,除了
∇
M
(
S
i
(
T
)
)
nabla Mleft( S_ileft( T right) right),
∇M(Si(T)),它表示地图的梯度。
∇
M
(
S
i
(
T
)
)
nabla Mleft( S_ileft( T right) right),
∇M(Si(T))的求解需要对地图进行插值。其中插值方法为双三次插值,预计参考下一篇新开博客。
Ⅴ CLOSING LOOPS
本篇的分枝定界是达到实时的重要方法(可以对比Hector-SLAM)
- 回环检测的目的:大场景种创建小的子图来抑制误差的累积。短时间内,连续激光数据组成的子图误差小。但是不同子图的误差消除需要进行回环检测来优化位姿(将位姿之间的差值转换成最小二乘来求解)。
SPA:

SPA指的是:Sparse Pose Adjustment,即稀疏姿态调整公式。
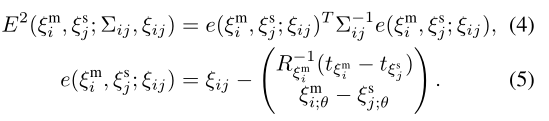
e为残差。原文提到如果扫描匹配的优化问题中出现异常值,损失函数
ρ
rho
ρ(例如Huber损失函数)可以用来减少SPA公式中可能出现异常值的影响。Huber robust error function:
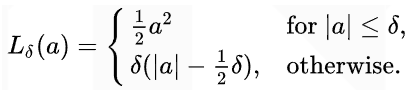
关于Huber损失函数:鲁棒性回归的损失函数,相比平方误差损失,Huber损失对于数据中异常值的敏感性要差一些。在值为0时,它也是可微分的。它基本上是绝对值,在误差很小时会变为平方值。误差使其平方值的大小如何取决于一个超参数δ,该参数可以调整。当δ~ 0时,Huber损失会趋向于MAE;当δ~
∞
infty
∞(很大的数字),Huber损失会趋向于MSE。
其中a可以表示为residuals(残差),如果残差比较小,可以进行Huber第一个平方操作,如果残差较大,直接通过公式1引入会引导到错误方向。因此,通过公式2中线性化操作,避免引入较大残差项(主要避免对称环境中,减小误差匹配带来的问题)。
pixel-accurate match:精确像素匹配
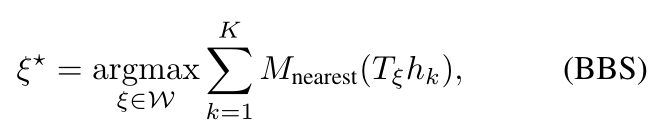
其中,
W
W
W是搜索窗口,
M
n
e
a
r
e
s
t
M_{nearest}
Mnearest是通过将其参数四舍五入到最近的网格点来扩展到所有的像素(前端CSM基础上,又进行了回环的进一步匹配,精确度可以达到像素级别)。
仔细确定步长可以提高搜素效率,以角度步长为
δ
θ
delta theta
δθ,从而在最大范围
d
m
a
x
d_{max}
dmax处的扫描点移动不超过一个像素的宽度
r
r
r.利用余弦定理,我们推出
d
max
=
max
k
=
1
,
…
K
∥
h
k
∥
d_{max},,=,,underset{k=1,…K}{max}left| h_k right|
dmax=k=1,…Kmax∥hk∥
δ
θ
=
a
r
c
cos
(
1
−
r
2
2
d
max
2
)
delta _{theta}=arccos left( 1-frac{r^2}{2d_{max}^{2}} right)
δθ=arccos(1−2dmax2r2)
计算覆盖给定线性和角度搜索窗口大小的整数步长,比如窗口为
W
x
=
W
y
=
7
c
m
,
W
θ
W_x=W_y=7cm,W_theta
Wx=Wy=7cm,Wθ=30°。
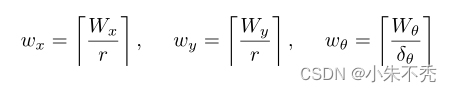
这就导致围绕其中心的估计位姿
ξ
0
xi _0
ξ0形成搜索窗口的一个有限集W
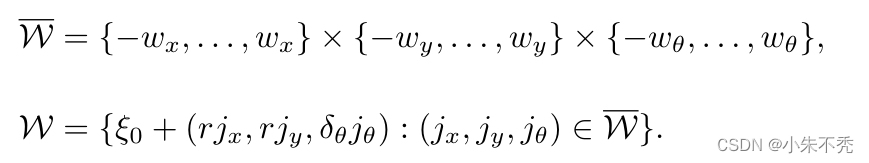
围绕我们问题的需要,很容易形成一个普通的暴力算法。但是,因为如果pure localization error太大的话,形成窗口也很大,三层for循环搜索的速度太慢

因此,本文利用分枝定界来加速(实际测评比起普通暴力方法,可能达到6倍速)计算
ξ
∗
xi ^*
ξ∗,分枝定界的思想是将可能的子集表示为树中的节点,其中根节点表示所有可能方法,在上述例子中是W。父节点是所有子节点及以下部分的分枝上界(upper bound),即每当一个节点有解时,比如打分30,那么子树中就不存在比这个30更优的解。为了得到这个分枝定界的具体算法,我们必须确定节点选择、分枝和上界的计算方法:
(1)在节点选择方面:在没有更好选择情况下,选用DFS(深度优先)作为默认选择。
(2)在分枝方面:树的每一个节点由一组整数c = (
c
x
c_x
cx,
c
y
c_y
cy,
c
θ
c_θ
cθ,
c
h
c_h
ch)∈
Z
4
Z^4
Z4,
c
h
c_h
ch表示当前节点所处的层级。ch层的节点有
2
c
h
∗
2
c
h
2^{ch}*2^{ch}
2ch∗2ch(即每个节点均分出4个子节点)种可能的平移,但只有特定的旋转。当叶子节点ch = 0时,一个可行解为
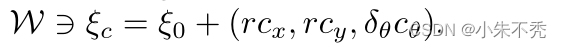

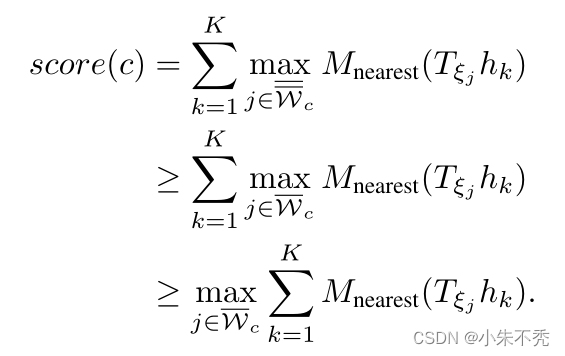
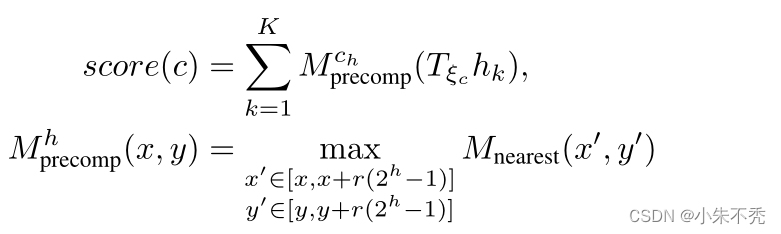
这部分为通过预计算网格进行上界的搜索过程


算法2和3为分枝及搜索best_score的过程,其中best_score只能由叶子节点的值进行更新。
本文前面关于流程图的描述还需持续更正、有错误的地方会持续纠正。参考
深蓝学院《激光SLAM》前端帧间匹配及计算机视觉life关于Cartographer论文解读部分。
最后
以上就是大意百褶裙最近收集整理的关于Cartographer原文阅读ABSTRACTⅠINTRODUCTIONⅡ RELATED WORKⅢ SYSTEM OVERVIEWⅣ LOCAL 2D SLAMⅤ CLOSING LOOPS的全部内容,更多相关Cartographer原文阅读ABSTRACTⅠINTRODUCTIONⅡ内容请搜索靠谱客的其他文章。








发表评论 取消回复