本文总结机器学习基石的第二次作业,主要包括VC Bound、Growth Function和VC Dimention的相关理解,以及Decision Stump的实现。
前两个问题考虑目标中存在噪声的情况。
假设存在一个似然函数
h
h
h能够近似一个确定的目标函数
f
f
f,且输出错误(即
h
(
x
)
≠
f
(
x
)
h(x)neq f(x)
h(x)=f(x))的概率为
μ
mu
μ(注:
h
h
h和
f
f
f的输出均为
{
−
1
,
+
1
}
{-1,+1}
{−1,+1},如果用
h
h
h去近似一个含噪声的
f
f
f(用
y
y
y表示),如下所示:
P
(
x
,
y
)
=
P
(
x
)
P
(
y
∣
x
)
P
(
y
∣
x
)
=
{
λ
,
y
=
f
(
x
)
1
−
λ
,
o
t
h
e
r
w
i
s
e
P(x,y)=P(x)P(y|x) \ P(y|x)=begin{cases}lambda, y=f(x)\1-lambda, otherwiseend{cases}
P(x,y)=P(x)P(y∣x)P(y∣x)={λ, y=f(x)1−λ, otherwise

用 h h h近似带噪声的目标 y y y的错误率为多少?
h h h 和 y y y 通过 f f f 联系在一起,因此错误的情况分为两种:
- h = f , f ≠ y h=f, fneq y h=f, f=y,错误率: P 1 = ( 1 − μ ) ( 1 − λ ) P1=(1-mu)(1-lambda) P1=(1−μ)(1−λ) ;
- h ≠ f , f = y hneq f, f=y h=f, f=y,错误率: P 2 = μ λ P2=mu lambda P2=μλ;
所以最终的错误率为 P = ( 1 − μ ) ( 1 − λ ) + μ λ P=(1-mu)(1-lambda)+mulambda P=(1−μ)(1−λ)+μλ

当 λ lambda λ取何值时,似然函数 h h h 与 μ mu μ 无关?
化简问题1中的结果: P = ( 2 λ − 1 ) μ − λ + 1 P=(2lambda-1)mu-lambda+1 P=(2λ−1)μ−λ+1,因此当 λ = 1 / 2 lambda=1/2 λ=1/2时,上式与 μ mu μ无关。
问题3-5是关于泛化误差的理解,以及如何获得数值上界。主要涉及VC Bound 理论:
P D [ ∣ E i n ( g ) − E o u t ( g ) ∣ > ϵ ] ≤ 4 ( 2 N ) d v c e x p ( − 1 8 ϵ 2 N ) mathbb{P}_D[|E_{in}(g)-E_{out}(g)|gtepsilon]le 4(2N)^{d_{vc}}exp(-frac{1}{8}epsilon^2N) PD[∣Ein(g)−Eout(g)∣>ϵ]≤4(2N)dvcexp(−81ϵ2N)

对于一个
d
v
c
=
10
d_{vc}=10
dvc=10 的假设空间/似然函数集
H
H
H,如果使其泛化误差
ϵ
≤
0.05
epsilonle0.05
ϵ≤0.05 的概率大于
95
%
95%
95%,则哪个数据量与该条件最接近?
代入数据可以发现, 460000 460000 460000 最接近。
代码实现:
'''
使用sympy.solve函数解方程,需要传入两个参数:
第1个参数是方程的表达式(把方程所有的项移到等号的同一边的式子),
第2个参数是方程中的未知数。
函数的返回值是一个列表,代表方程的所有根(可能为复数根)。
'''
import sympy
N = sympy.symbols('N') # 声明求解变量
err = 0.05
dvc = 10
epsilon = 0.05
result = sympy.solve([4 * (2*N)**dvc * sympy.exp(-(1/8) * epsilon**2 * N) - err], N)
print(result)
# 计算结果
'''
[(-0.322594253962319,), (0.322600758284254,), (452956.864723099,), (-0.260985859768725 - 0.189614963554584*I,), (-0.260985859768725 + 0.189614963554584*I,), (-0.0996907427335785 - 0.306806548691186*I,), (-0.0996907427335785 + 0.306806548691186*I,), (0.0996854806265985 - 0.306810371835693*I,), (0.0996854806265985 + 0.306810371835693*I,), (0.260987869714738 - 0.189621149532343*I,), (0.260987869714738 + 0.189621149532343*I,)]
'''
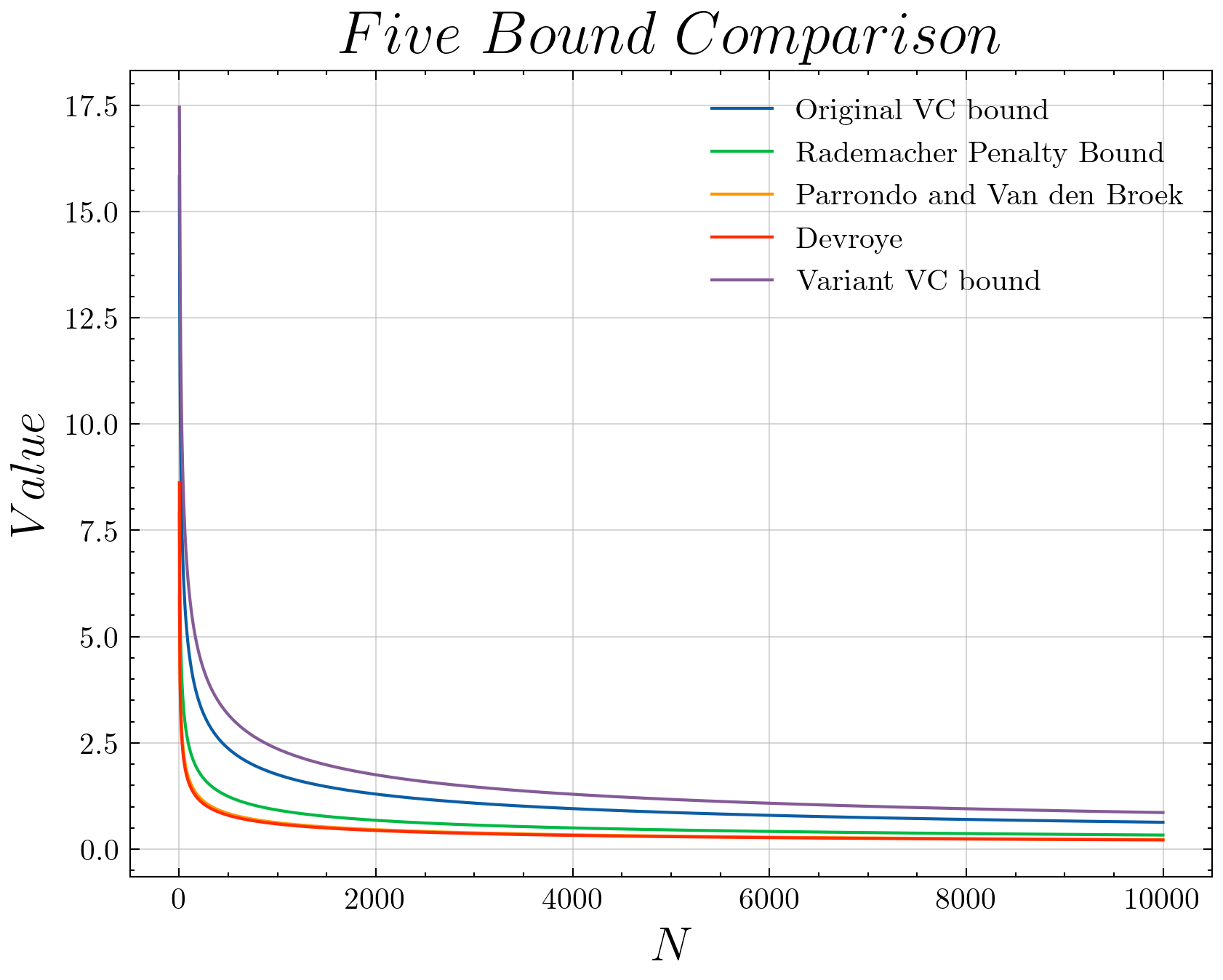
除了VC Bound之外,还有许多其它的Bounds准则,主要有以下5种:

假设 d v c = 50 , δ = 0.05 d_{vc}=50, delta=0.05 dvc=50, δ=0.05,则对于不同的 N N N(10000和5),各Bounds中哪个值最小?
通过编程实现(完整代码在文末),输出如下:
Original VC bound (10000) and (5):
0.6322033623117665 13.828161484991483
Rademacher Penalty Bound (10000) and (5):
0.3313236947803298 7.048776564183685
Parrondo and Van den Broek (10000) and (5):
0.2237083662461448 5.101361981989993
Devroye (10000) and (5):
0.21523765672535045 5.593125543182669
Variant VC bound (10000) and (5):
0.8604643458940426 16.264111061012045
对于
N
=
10
,
000
N=10,000
N=10,000的情况Devroye最小,对于
N
=
5
N=5
N=5的情况parrondo最小。

对于
N
=
10
,
000
N=10,000
N=10,000的情况Devroye最小,对于
N
=
5
N=5
N=5的情况parrondo最小。
问题6-问题11,主要考察growth function和VC维。
问题6-7的题设:求“positive-and-negative intervals on R”(在区间 [ l , r ] [l, r] [l,r]之间为 + 1 +1 +1,其余为 − 1 -1 −1;或在区间 [ l , r ] [l, r] [l,r]之间为 − 1 -1 −1,其余为 + 1 +1 +1)这种类型似然函数集的 growth function( m H ( N ) m_H(N) mH(N))和VC维?成长函数的定义是:对于由N个点组成的不同集合中,某集合对应的dichotomy最大,那么这个dichotomy值就是 m H ( H ) m_H(H) mH(H),它的上界是 2 N 2^N 2N。
| 成长函数 | 计算公式 |
|---|---|
| 正射线(Positive rays) | m H ( N ) = N + 1 m_H(N) = N+1 mH(N)=N+1 |
| 一维空间感知器 | m H ( N ) = 2 N m_H(N)=2N mH(N)=2N |
| 间隔为正的分类(Positive intervals) | m H ( N ) = 1 2 N 2 + 1 2 N + 1 m_H(N)=frac{1}{2}N^2 + frac{1}{2}N + 1 mH(N)=21N2+21N+1 |
| 凸分布 | m H ( N ) = 2 N m_H(N)=2^N mH(N)=2N |
| 二维平面感知器 | m H ( N ) < 2 N m_H(N)<2^N mH(N)<2N |
突破点(break point):不能满足完全分类情形的样本点个数。完全二分类(shattered)是可分出 2 N 2^N 2N 种二分类(dichotomy)的情形。

上述问题可以看成N个数据,之间有N-1个空隙,扩展左边空隙变为N个空隙,则任选两个空隙
C
N
2
C_N^2
CN2,则有
2
C
N
2
2C_N^2
2CN2种分法。但这样还少了全+1和全-1的情况,所以总共应该有
N
(
N
−
1
)
+
2
=
N
2
−
N
+
2
N(N-1)+2=N^2-N+2
N(N−1)+2=N2−N+2种。

由于已经有了成长函数
m
h
(
N
)
m_h(N)
mh(N),所以可以直接计算break point,n=3时m=8,n=4时m=14
→
rightarrow
→ k=4
→
rightarrow
→
d
v
c
=
3
d_{vc}=3
dvc=3。(VC维
<
2
N
lt 2^N
<2N)

二维空间上,“甜甜圈”类型的似然函数集(如下图所示),在甜甜圈内部为+1(
a
2
≤
x
1
2
+
x
2
2
≤
b
2
a^2le x_1^2+x_2^2leq b^2
a2≤x12+x22≤b2),外部为-1,假设
0
<
a
<
b
<
inf
0<a<b<inf
0<a<b<inf,求其growth function?
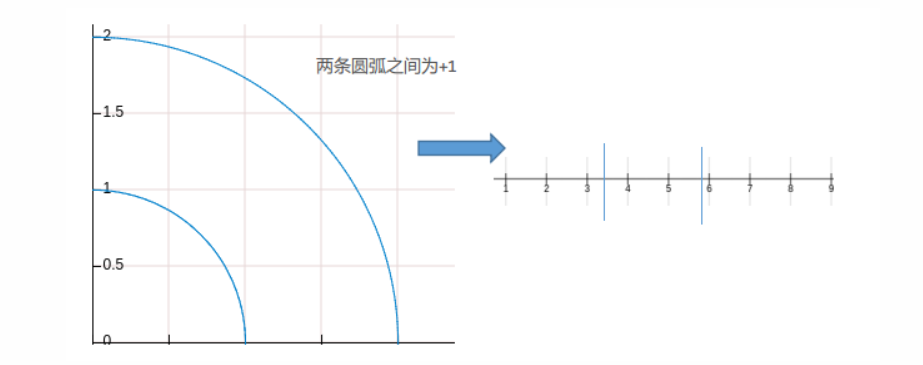
可以将其转换为1维情况来看,对于
r
r
r 相等的所有数据点视为相同,则问题就转换为一维类似Q6中的情况(但条件变了),似然函数集等价于
[
l
,
r
]
[l, r]
[l,r]之间为+1,其他地方为-1。从而类似的分析可得growth function为
C
N
+
1
2
+
1
C_{N+1}^2+1
CN+12+1(分析时两边都扩展空隙,+1来自于全部数据标签为-1的情况)。
考虑“多项式判别表达式”函数集在一维空间
R
mathbb{R}
R上的VC维为多少?(似然函数集如下)

本质上就等同于Lecture7(9/26)上的d维的perceptron,(可以令
x
i
=
x
i
x_i=x^i
xi=xi,从而转化为高维空间上的感知机问题)由PPT上结果可知
d
v
c
=
D
+
1
d_{vc}=D+1
dvc=D+1(由该题目可知:n 次方程最多有 n 个不重根,可将一维空间划分为 n+1 段;易知:一维空间被划分为K个子区域(每个区域均可加可减),对应的
d
v
c
=
K
d_{vc}=K
dvc=K)。
考虑d维空间
R
d
mathbb{R}^d
Rd上“简单决策树”似然函数集的VC维。似然函数集如下所示:

其中,通过d个阈值
t
i
(
i
=
1
,
.
.
.
d
)
t_i(i=1,...d)
ti(i=1,...d),将数据
x
x
x划分到集合S中的一个区域中去,从而
x
x
x 的标签可以根据其是否在某块区域确定。求该似然函数集的VC维?
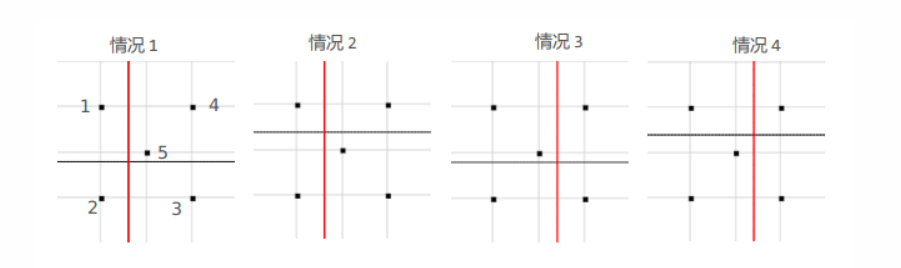
可以先从两个特例出发:
-
① d = 1 d=1 d=1时的情况,可以看成 S = { 0 } , { 1 } , { 0 , 1 } , { } S={0},{1},{0,1},{} S={0},{1},{0,1},{},从而根据 t t t的移动可以等价为双向射线的情况( S = { 0 , 1 } { } S={0,1}{} S={0,1}{}可以视为另外两种的子情况),则对应的 m ( N ) = 2 N m(N)=2N m(N)=2N, d v c = 2 d_{vc}=2 dvc=2。(也可直接根据Q9得到结果)
-
② d = 2 d=2 d=2时的情况,相当于通过两条线(一条与x轴平行,一条与y轴平行)将空间划分为四个区域,每个区域均可加可减(互相独立),且这两条直线可上下左右移动(相当于改变阈值 t i t_i ti),显然,对于 N = 4 N=4 N=4可以shatter,对于 N = 5 N=5 N=5可以划分为四大类:
- a. (4,5)一起,则共有 s 1 = 2 4 = 16 s1=2^4=16 s1=24=16
- b. (3,5)一起,则共有 s 2 = 2 × 2 2 = 8 s2=2times 2^2=8 s2=2×22=8(去除了(4,5)同号情况)
- c. (1,5)一起,则共有 s 3 = 4 s3=4 s3=4
- d. (2,5)一起,则共有 s 4 = 2 s4=2 s4=2
所以总共有 s = 16 + 8 + 4 + 2 = 30 ≠ 2 5 = 32 s=16+8+4+2=30neq 2^5=32 s=16+8+4+2=30=25=32,因此 N = 5 N=5 N=5不能被shatter(因为图中情况属于“最佳可分”情况,所以可以不检验其他情况)。从中也可以得出一个结论,如果某个点无法单独存在于子区域中,则不可能shatter。
-
③ d = M d=M d=M的情况,此时整个空间可以被划分为 2 M 2^M 2M个子区域,由上述分析易知, N = 2 M N=2^M N=2M可以被shatter,而 N = 2 M + 1 N=2^M+1 N=2M+1不能被shatter。
综上所属:该问的答案为 d v c = 2 d d_{vc}=2^d dvc=2d。
考虑一维空间上“三角波”似然函数集的VC维。三角波似然函数集如下所示:

其中
z
m
o
d
4
∈
[
0
,
4
)
z mod 4in[0,4)
z mod 4∈[0,4) 代表取余数。

通过简单的运算不难发现,该似然函数集相当于一个方波(如图所示),该方波有两个特点,关于y轴对称,周期可以随意缩放,这样就相当于将
R
mathbb{R}
R划分为无限段区域。由于周期可以为任意正实数,所以甚至可以近乎无限小。根据Q9的结论易知该情况
d
V
C
=
∞
d_{VC}=infty
dVC=∞。举个例子,如
N
=
3
N=3
N=3时,缩小则3变为-1,放大则1变为-1,缩小到一定程度能够使得1,3变为-1,总之可以根据缩放达到任意我们希望的+1,-1组合。
问题12-15:主要对growth function
m
H
(
N
)
m_H(N)
mH(N) 和VC维性质和界限的考察(这些均指
Y
∈
{
+
1
,
−
1
}
mathbb{Y}in{+1,-1}
Y∈{+1,−1})。

以下哪项是
N
≥
d
v
c
≥
2
Nge d_{vc}ge 2
N≥dvc≥2情况下
m
H
(
N
)
m_H(N)
mH(N)的上界?
增加一个数据,最多增加2倍可能(即+1,-1),从而可知 m H ( N ) ≤ 2 m H ( N − 1 ) ≤ 2 i m H ( N − i ) m_H(N)leq 2m_H(N-1)leq 2^im_H(N-i) mH(N)≤2mH(N−1)≤2imH(N−i),所以 c 项为 m H ( N ) m_H(N) mH(N)的上界。

以下哪一种growth function
m
H
(
N
)
m_H(N)
mH(N)是不可能出现的?
b项显然不可能,当 N = 2 N=2 N=2和 N = 3 N=3 N=3时是相等的,但 N = 4 N=4 N=4时却不同了,显然这不可能。其中有个结论:growth function是单调递增的。

有一系列似然函数集
H
1
,
H
2
,
.
.
.
,
H
K
mathcal{H}_1,mathcal{H}_2,...,mathcal{H}_K
H1,H2,...,HK,对应的VC维为
d
v
c
(
H
k
)
d_{vc}(mathcal{H}_k)
dvc(Hk),以下哪一个选项是这一系列似然函数集的交集
d
v
c
(
∩
k
=
1
K
H
k
)
d_{vc}(cap_{k=1}^Kmathcal{H}_k)
dvc(∩k=1KHk)的紧上下界限?
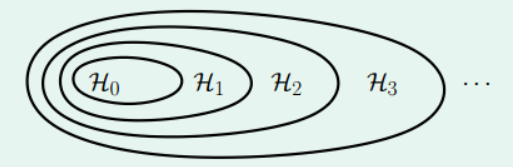
当全部
H
k
mathcal{H}_k
Hk均没有交集的情况下,则为
∅
emptyset
∅,从而下界为0,当为上图这种情况时交集为
H
0
mathcal{H}_0
H0,从而为
m
i
n
{
d
v
c
(
H
k
)
}
k
=
1
K
min{d_{vc}(mathcal{H}_k)}_{k=1}^K
min{dvc(Hk)}k=1K,因此答案为b。

以下哪一个选项是这一系列似然函数集的并集
d
v
c
(
∪
k
=
1
K
H
k
)
d_{vc}(cup_{k=1}^Kmathcal{H}_k)
dvc(∪k=1KHk)的紧上下界限?
显然并集包含最少似然函数的情况如上图所示,因此,下界为 m a x { d v c ( H k ) } k = 1 K max{d_{vc}(mathcal{H}_k)}_{k=1}^K max{dvc(Hk)}k=1K,上界可以根据一个特例来说明:有一个 H 1 mathcal{H}_1 H1,把平面所有点分为+1, H 2 mathcal{H}_2 H2把平面所有点分为-1。 H 1 mathcal{H}_1 H1并 H 2 mathcal{H}_2 H2的话为VC dimension为1,而各自 d v c d_{vc} dvc加起来为0。选 d 。
主要考察“一刀切”式的“决策树桩”算法。以下给出单维和多维情况下的算法的“口语化”说明。其中单维对应的式子:
h
s
,
θ
(
x
)
=
s
⋅
s
i
g
n
(
x
−
θ
)
h_{s,theta}(x)=scdot sign(x-theta)
hs,θ(x)=s⋅sign(x−θ)
多维情况对应的式子:
h
s
,
i
,
θ
=
s
⋅
s
i
g
n
(
x
i
−
θ
)
h_{s,i,theta}=scdot sign(x_i-theta)
hs,i,θ=s⋅sign(xi−θ)
算法说明

单维树桩算法
假定初始数据为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)} {(x1,y1),(x2,y2),...,(xN,yN)}
① 预先设定N个阈值 θ theta θ(先对数据的 x x x进行排序,将 θ theta θ设定为其间隙值,且取一个最小数左边的值)
② 计算每一个阈值 θ theta θ和 s = + 1 , − 1 s=+1,-1 s=+1,−1对应的 E i n E_{in} Ein,找出其中对应最小 E i n E_{in} Ein的 θ , s theta, s θ, s
返回 θ , s , m i n E i n theta, s, minE_{in} θ, s, minEin
其中①中可以采用其他的策略来实现,但具体方式是相近的。
多维树桩算法
假定初始数据为 { ( x ( 1 ) , y ( 1 ) , ( x ( 2 ) , y ( 2 ) , . . . , ( x ( N ) , y ( N ) } {(x^{(1)},y^{(1)},(x^{(2)},y^{(2)},...,(x^{(N)},y^{(N)}} {(x(1),y(1),(x(2),y(2),...,(x(N),y(N)},其中 x ( i ) ∈ R d x^{(i)}inmathbb{R}^d x(i)∈Rd
①For i=1,2,…,d:
寻找维度i情况下的 θ , s , m i n E i n theta, s, minE_{in} θ, s, minEin(通过单维树桩的方式求得)
②寻找上述 d d d个不同 m i n E i n minE_{in} minEin中最小的那个,以及对应的 θ , s theta, s θ, s(如果存在两个 m i n E i n minE_{in} minEin相同则任意取一个)
返回 θ , s , m i n E i n theta, s, minE_{in} θ, s, minEin


对于任意一个决策树桩函数 h s , θ θ ∈ [ − 1 , + 1 ] h_{s,theta} thetain[-1,+1] hs,θ θ∈[−1,+1],其对应的 E o u t ( h s , θ ) E_{out}(h_{s,theta}) Eout(hs,θ)为以下哪一种函数?
为简便起见,假设 s = 1 , θ > 0 s=1,thetagt0 s=1,θ>0,此时 h h h预测情况: [ θ , 1 ] → + 1 [theta,1]to +1 [θ,1]→+1, [ − 1 , θ ] → − 1 [-1,theta]to-1 [−1,θ]→−1, f f f真实情况: ( p = 0.8 ) [ − 1 , 0 ] → − 1 (p=0.8)[-1,0]to-1 (p=0.8)[−1,0]→−1, ( p = 0.2 ) [ − 1 , 0 ] → + 1 (p=0.2)[-1,0]to+1 (p=0.2)[−1,0]→+1, ( p = 0.8 ) [ 0 , 1 ] → + 1 (p=0.8)[0,1]to+1 (p=0.8)[0,1]→+1, ( p = 0.2 ) [ 0 , 1 ] → − 1 (p=0.2)[0,1]to-1 (p=0.2)[0,1]→−1。从而可见错误出现在区间 [ 0 , θ ] [0,theta] [0,θ]错误概率为 0.8 0.8 0.8,其他区域错误概率为 0.2 0.2 0.2。因此 E o u t = ( 0.2 ( 2 − θ ) + 0.8 θ ) / 2 = 0.2 + 0.3 θ E_{out}=(0.2(2-theta)+0.8theta)/2=0.2+0.3theta Eout=(0.2(2−θ)+0.8θ)/2=0.2+0.3θ,其他三种情况类似分析,最终可得答案为c。
根据规则随机生成20组数据,运行5,000次,求平均
E
i
n
E_{in}
Ein和平均
E
o
u
t
E_{out}
Eout(其中
E
o
u
t
E_{out}
Eout由Q16中的答案来求解)?

训练集平均误差: 0.17055

测试集平均误差: 0.265751858602122
求多维决策树桩在训练集和测试集上的误差
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout?

训练集误差: 0.25

测试集误差: 0.355
相关代码:
'''
Q5
'''
n = np.arange(3, 10000)
f1 = np.sqrt(8/n*(np.log(80)+50*np.log(2*n)))
print('Original VC bound (10000) and (5): n', f1[-1], 't', f1[2])
f2 = np.sqrt(2/n*(np.log(2*n)+50*np.log(n)))+np.sqrt(2/n*math.log(20))+1/n
print('Rademacher Penalty Bound (10000) and (5): n', f2[-1], 't', f2[2])
f3 = 1/n+np.sqrt(1/np.power(n, 2)+1/n*(np.log(120)+50*np.log(2*n)))
print('Parrondo and Van den Broek (10000) and (5): n', f3[-1], 't', f3[2])
f4 = 1/(n-2)+np.sqrt(1/np.power(n-2, 2)+1/(2*n-4)*(np.log(80)+100*np.log(n)))
print('Devroye (10000) and (5): n', f4[-1], 't', f4[2])
f5 = np.sqrt(16/n*(np.log(2/math.sqrt(0.05))+50*np.log(n)))
print('Variant VC bound (10000) and (5): n', f5[-1], 't', f5[2])
plt.cla()
plt.style.use('science') # 已经配置好 SciencePlot,可参考上一篇文章;如果没配置,可以换为别的风格,比如ggplot。
plt.plot(n, f1, label='Original VC bound')
plt.plot(n, f2, label='Rademacher Penalty Bound')
plt.plot(n, f3, label='Parrondo and Van den Broek')
plt.plot(n, f4, label='Devroye')
plt.plot(n, f5, label='Variant VC bound')
plt.xlabel('$N$', size=16)
plt.ylabel('$Value$', size=16)
plt.title('$Five Bound Comparison$', size=20)
plt.grid(linestyle='-', alpha=0.5)
plt.legend()
plt.savefig('Q5.png', dpi=300)
plt.close('all')
def load_data(filename):
'''
读取数据
'''
data = pd.read_csv(filename, sep='s+', header=None)
row, col = data.shape[0], data.shape[1] # 获取行数和列数;shape=(400,5)
# np.c_:按【列】连接两个矩阵,要求行数相等。np.r_:按【行】连接两个矩阵,要求列数相等;
# 由题设可知,前4行为数据x;并要求添加偏差1,通过np.ones((col, 1))实现;
X = np.c_[np.ones((row, 1)), data.iloc[:, 0:col-1]]
# 最后一行为期望输出y;
y = data.iloc[:, col-1:col].values
return X, y
def generate_data():
'''
生成数据
'''
x = np.random.uniform(-1, 1, 20)
y = np.sign(x)
y[y == 0] = -1
prop = np.random.uniform(0, 1, 20)
y[prop >= 0.8] *= -1
return x, y
# 单维度决策树桩算法
def decision_stump(X, y):
theta = np.sort(X)
num = len(theta)
Xtemp = np.tile(X, (num, 1))
ttemp = np.tile(np.reshape(theta, (num, 1)), (1, num))
ypred = np.sign(Xtemp - ttemp)
ypred[ypred == 0] = -1
err = np.sum(ypred != y, axis=1)
if np.min(err) <= num-np.max(err):
return 1, theta[np.argmin(err)], np.min(err)/num
else:
return -1, theta[np.argmax(err)], (num-np.max(err))/num
# 多维度决策树桩算法
def decision_stump_multi(X, y):
row, col = X.shape
err = np.zeros((col,)); s = np.zeros((col,)); theta = np.zeros((col,))
for i in range(col):
s[i], theta[i], err[i] = decision_stump(X[:, i], y[:, 0])
pos = np.argmin(err)
return pos, s[pos], theta[pos], err[pos]
# Q17 & Q18
totalin = 0; totalout = 0
for i in range(5000):
X, y = generate_data()
theta = np.sort(X)
s, theta, errin = decision_stump(X, y)
errout = 0.5 + 0.3 * s * (math.fabs(theta)-1)
totalin += errin
totalout += errout
print('训练集平均误差: ', totalin/5000)
print('测试集平均误差: ', totalout/5000)
输出:
训练集平均误差: 0.17055
测试集平均误差: 0.265751858602122
# Q19 & Q20
X, y = load_data('hw2_train.dat')
testX, testy = load_data('hw2_test.dat')
pos, s, theta, err = decision_stump_multi(X, y)
print('训练集误差: ', err)
ypred = s * np.sign(testX[:, pos]-theta)
ypred[ypred == 0] = -1
row, col = testy.shape
errout = np.sum(ypred != testy.reshape(row,))/len(ypred)
print('测试集误差: ', errout)
输出:
训练集误差: 0.25
测试集误差: 0.355
参考:
机器学习基石作业2:https://github.com/AceCoooool/MLF-MLT
机器学习基石作业2:https://www.cnblogs.com/wanderingzj/p/4950578.html
最后
以上就是矮小诺言最近收集整理的关于机器学习基石作业02:Growth Function、VC Dimention、Decision Stump的全部内容,更多相关机器学习基石作业02:Growth内容请搜索靠谱客的其他文章。








发表评论 取消回复